
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Множення одночлена на многочленСодержание книги
Поиск на нашем сайте
Помножимо одночлен 2 а на многочлен а 2 - 3 а + 4. Використовуючи розподільний закон множення, матимемо: 2 а (а 2 - 3 а + 4) = 2 а × а 2 - 2 а × 3 а + 2 а × 4 = 2 а 3 - 6 а 2 + 8 а. Отже, добутком одночлена 2 а і многочлена а 2 - 3 а + 4 є многочлен 2 а 3 - 6 а 2 + 8 а. Щоб знайти добуток, ми помножили одночлен на кожний член многочлена й одержані результати додали.
За цим правилом можна множити і многочлен на одночлен. Наприклад: (3 х 2 - х + 2) × 3 х = 3 х 2 × 3 х - х × 3 х + 2 × 3 х = 9 х 3 - 3 х 2+ 6 х. Добуток будь-якого одночлена і будь-якого многочлена завжди можна записати у вигляді многочлена.
Приклад 1. Виконати множення: а) 2 a 2 b × (-5 b 2 + 2 ab); б) (2 a + b - 3 c) × (-4 а). ● а) 2 a 2 b × (-5 b 2 + 2 ab) = 2 a 2 b × (-5 b 2) + 2 a 2 b × 2 ab = -10 a 2 b 3 + 4 a 3 b 2. Скорочений запис: 2 a 2 b × (-5 b 2 + 2 ab) = -10 a 2 b 3 + 4 a 3 b 2. б) (2 a + b - 3 c) × (-4 а) = 2 a × (-4 а) + b × (-4 а) - 3 c × (-4 а) = = -8 a 2- 4 аb + 12 ас. Скорочений запис: (2 a + b - 3 c) × (-4 а) = -8 a 2- 4 аb + 12 ас. ● Приклад 2. Спростити вираз 5 х (х 2 + 4 х - 2) - 2 х 2(3 х - 1). ● 5 х (х 2 + 4 х - 2) - 2 х 2(3 х - 1) = = - х 3 + 22 х 2 - 10 х. ● Приклад 3. Розв’язати рівняння 2 х (2 х + 3) - 7 = 4 х 2 - 4. ● 4 х 2 + 6 х - 7 = 4 х 2 - 4; 4 х 2 + 6 х - 4 х 2 = 7 - 4; 6 х = 3; х = 0,5. Відповідь. 0,5. ● Усно 388. Виконайте множення: a) a (а + 1); б) а (а 2 - 2 a); в) х (х 2 + х - 4); г) (a + 4) × a; д) (b + 2 a) × b; е) (y 2 + 4 y + 4) × y.
Перемножте вирази: 389. а) х (2 х - 5); б) 2 а 2(5 а + 3); в) b (4 b 2 + 3 b); г) - а 2(a 2 - 2 a + 1); д) 4 с 2(2 с 3 - с 2+ 5); е) - аb (2 a - 3 b - 2); є) (х 2 - 5 х) × х 2; ж) (- y 3+ 5 y 3) × (-4 y); з) (y 2 - x - 3) × 2 xy. 390. а) а (2 а + 3); б) 3 х (х 2 - 4 х + 3); в) -2 b (b 2 + 2 b - 3); г) 3 с 2(-2 с 4+ с 2 + 3); д) (-3 n 2+ 2 n) × 2 n; е) (2 a 2 - 2 a - 5) × (-3 a). Запишіть у вигляді многочлена стандартного вигляду: 391. a) - х (4 х - 3) + 3; б) (5 а + 2) × (-4 а) + 10 а 2; в) a 2(2 a 3 + а) - 2 a 3; г) 4 x (2 x - 3 x 2) - 8 x 2- 2 x. 392. а) -3 а 2(а - 1) - 3 а 2; б) 2 b (3 b 2 - 2) - 2 b 3 + 1. Спростіть вираз: 393. а) a (2 a + b) - ab; б) 4 y (2 x - y) - 8 xy + 2 y 2; в) 2(4 т 2 - 3) + m (-8 m - 3); г) - х (2 x - y) - (-2 x 2 + xy). 394. а) c (c 2 + 3 с) - 3 c 2; б) -5 х (x 2 + 3 х - 4) - 20 х; в) 2 а (3 а -4 b) + 8 аb - 2 а 2; г) -4 аb + 2 а (2 b + 3) - 6 а. Розв’яжіть рівняння: 395. а) 2(2 х - 1) + 3 = х - 2; б) 9 - 4(1 - 2 х) = 10 х; в) -1,5(6 х + 1) + 3 х = 3; г) 4 х (1 - 2 х) + 8 х 2 = 24. 396. а) 2 + 3(5 х - 3) = 8 х; б) 24 - 2(2 х + 6) = х.
Спростіть вираз: 397. а) 2 a (- а + 2 а 2) - 4(а 3 + 2 a - 2); б) 5 x 3(3 x 3- 2 x + 1)- x 2(8 x 2+ 5 x);
в) -8 m 3 n (mn 2 - mn - n 2)- (2 mn)3; г) 2 xy 2 - д) 2 ab (5 c + 2 а)- a (4 ab - bc); е) -5 x 3 y (2 x 2 y +4 y 3 x)-4 x 4(2 xy 2-5 y 4). 398. а) a 2(1 + 2 a + b 2) - (a 2 b 2 + a 2); б) 4 xy (2 x - y) - 2 х (4 xy - 1); в) -2 т 2 n 3(4 mn 2 - 8 m 2 n) -(4 т 2 n 2)2; г) 399. Доведіть, що для всіх значень х вираз x 2(x - 2) - x (x 2 + 2) + 2 x (1 + x) + 3 набуває одного й того ж значення. 400. Доведіть, що значення виразу x (x 2 + 2 y) - y (y + x) + y (y - x) не залежать від значень y. 401. Доведіть, що для кожного від’ємного значення а значення виразу 402. Доведіть, що для будь-яких значеннь х, y та z значення виразу Доведіть тотожність: 403. а) a (b - c) + b (c - a) + c (a - b) = 0; б) a (b 2 - bc + c 2) + ab (c - b) + ac (b - c) = abc; в) х 4(х 3 - х 2) - х 3(х 4 - х 3) + х 2(х 5 - х 4) - х (х 6 - х 5) = 0; г) ab (c - ab) + bc (a - bc) + ca (b - ca) + a 2 b 2 + b 2 c 2 + c 2 a 2 = 3 abc. 404. а) x (x - yz) + y (y - zx) + z (z - xy) + 3 xyz = x 2 + y 2 + z 2; б) a (a 4- 2 a 3 + 3 a 2) - a 2(a 3- a 2 + 2 a) + a 3(a - 1) = 0. Розв’яжіть рівняння: 405. а) 5(3 х - 6) + 4(3 - 2 х) = 5 х - 8; б) 0,4(2 х - 7) + 1,2(3 х + 0,7) = 1,6 х; в) х (3 + 2 х + 4 х 2) - 2 х 2(2 х + 1) = 9; г) 2,5 х - 2 х (1,5 х + 1) = 1 – 3 х 2. 406. а) -5(4 х + 3) + 3 х = -12(х - 5); б) 9(х - 3) - 4(7 - 3 х) - 3 = –8 х; в) 3 х 2(х + 1) - (3 х 3 + 3 х 2 + х – 1) = 0; г) 1,2 х (х + 2) – 3(0,4 х 2 + 1) = 0,6. 407. а) 408. а) 409. Сума двох чисел дорівнює 10, а сума їх добутку і квадрата меншого 410.Знайдіть площу прямокутника за такими даними: його довжина у 2,4 разу більша від ширини; якщо ширину прямокутника збільшити на 2 см, то площа збільшиться на 24 см2. 411. Дано три ділянки прямокутної форми. Довжина першої ділянки удвічі більша від її ширини. Друга ділянка має таку ж ширину, як перша, а
412. Спростіть вираз (n ¾ натуральне число): а) xn + 2(xn + 3 - 1) - xn (xn + 5 - x 2); б) аn + 1(аn + 1 - 4) - аn (аn + 2 – 4 a + 1); в) xn (xn +1(xn + 2 + xn + 1(x 2 - x + 1))). 413. Доведіть тотожність: а (1 + а + а 2 + … + а 9 + а 10) - (1 + а + а 2 + … + а 9 + а 10) = а 11 - 1. 414. Доведіть, що значення виразу 3 xn + 2 уn + 1(2 x 2 у 3 - 4 xу + 6) - 2 xn + 1 уn (3 x 3 у 4 - 6 x 2 у 2 + 9 ху), де n ¾ натуральне число, не залежать від значень x і у. 415. Учні 7 класу прийшли до театру. В антракті всі вони побігли в буфет. Кожен хлопець купив пиріжок, а кожна дівчина ¾ булочку. Якби кожна дівчина купила пиріжок, а кожен хлопець ¾ булочку, то вони разом витратили б на 50 к. менше. Пиріжок дорожчий від булочки на 10 к. Кого було більше — хлопців чи дівчат — і на скільки більше?
416. У банці було 3 л спирту. З неї відлили х л спирту і долили таку ж кількість води. Потім, коли спирт і вода змішалися, з банки відлили х л суміші. Скільки літрів спирту залишилося в банці? Вправи для повторення 417. Перший автомобіль долає шлях між двома містами за 1,5 год, а другий ¾ за 1,2 год. Швидкість другого автомобіля більша від швидкості першого на 15 км/год. Знайдіть відстань між містами. 418. З міста А до міста В одночасно виїхали легковий автомобіль і автофургон. Коли через 2,5 год легковий автомобіль прибув до міста В, автофургону залишалося їхати до міста В ще 30 км. Знайдіть відстань між містами, якщо швидкість легкового автомобіля в 1,2 разу більша від швидкості автофургона.
420. Виконайте множення одночленів: а) 5 a 2 · 3 a 3; б) 0,2 a 3 b · 10 a; в) 2 ax · (–0,3 ax 2); г) 4 m · 3 m 2 n; д) –2 cd · (–3 c 4 d); е) 4 a 3 b · (–0,5 a 2 b 3). 421. Запишіть у вигляді виразу: а) добуток двочленів a – b і 2 a + b; б) добуток суми виразів 2 a і 3 b та їх різниці.
|
|||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 757; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.213.73 (0.01 с.) |

 Приклади розв’язання вправ
Приклади розв’язання вправ =
= Рівень А
Рівень А Рівень Б
Рівень Б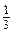 x (6 x + 6 y 2- 1) +
x (6 x + 6 y 2- 1) + 

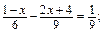 б)
б) 
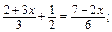 б)
б) 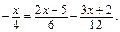
 Рівень В
Рівень В 419*. Пірати захопили скриню із золотими монетами й вирішили поділити здобич порівну. Якби піратів було на 10 менше, то кожному дісталося б монет в 1,2 разу більше. Скільки було піратів?
419*. Пірати захопили скриню із золотими монетами й вирішили поділити здобич порівну. Якби піратів було на 10 менше, то кожному дісталося б монет в 1,2 разу більше. Скільки було піратів?


