
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Степінь з натуральним показникомСодержание книги
Поиск на нашем сайте
Нагадаємо, що добуток двох або трьох однакових множників, кожен з яких дорівнює а, — це відповідно квадрат або куб числа а. Наприклад: 5 × 5 = 52; 52 — квадрат числа 5; 5 × 5 × 5 = 53; 53 — куб числа 5. Квадрат числа 5 називають ще другим степенем цього числа, а куб — третім степенем. Відповідно добуток 5 × 5 × 5 × 5 позначають 54 і називають четвертим степенем числа 5. У виразі 54 число 5 називають основою степеня, число 4 ¾ показником степеня, а весь вираз 54 називають степенем.
Степінь з основою а й показником п записують так: аn, читають: «а в степені п», або «n -ий степінь числа а». Отже, за означенням
а 1 = а. З’ясуємо знак степеня з натуральним показником. 1) а = 0, тоді 01 = 0, 02 = 0 × 0 = 0,... ¾ будь-який натуральний степінь числа 0 дорівнює 0. 2) а > 0, тоді а 1 = а > 0, а 2 = аa > 0,... ¾ будь-який натуральний степінь додатного числа є число додатне. 3) а < 0, тоді а 1 = а < 0, а 2 = аa > 0, а 3 = аaa < 0, а 4 = ааaa > 0,.... Степінь від’ємного числа з парним показником є число додатне, оскільки добуток парного числа від’ємних чисел додатний. Степінь від’ємного числа з непарним показником є число від’ємне, оскільки добуток непарного числа від’ємних чисел від’ємний. Підносити числа до степеня з натуральним показником можна за допомогою мікрокалькулятора. Обчислити, наприклад, значення 3,56 можна за схемою:
або за більш зручною схемою:
Піднесення до степеня — дія третього ступеня. Нагадаємо, що коли вираз без дужок містить дії різних ступенів, то спочатку виконують дії вищого ступеня, відтак — нижчого. Так, щоб знайти значення виразу 2 × 32 – 64,
Приклад 1. Обчислити 4 × (-5)3 + 8 × 0,5. ● Виконуючи обчислення, можна: а) записувати кожну дію окремо: 1) (-5)3 = -125; 2) 4 × (-125) = -500; 3) 8 × 0,5 = 4; 4) -500 + 4 = -496; б) записувати обчислення в рядок: 4 × (-5)3 + 8 × 0,5 = 4 × (-125) + 4 = -500 + 4 = -496. Відповідь. -496. ●
Усно 233. Прочитайте вирази, назвіть основи й показники степенів: а 12; (-3)4; (-0,05)20; m 9; 3 m; 234. Обчисліть: 17; 24; (-2)4; 33; (-3)3; (-5)2; 43; 235. Значення яких степенів є додатними; від’ємними: (-7)4; (-11)3; 156; (-21)2; 33; 1731; (-1,5)20; (-0,05)11?
Запишіть добуток у вигляді степеня: 236. а) 4 × 4 × 4 × 4 × 4 × 4; б) в) д) (- b) × (- b) × (- b) × (- b); е) (х - y) × (х - y) × (х - y). 237. а) (-5) × (-5) × (-5) × (-5); б) в) 238. Запишіть степінь у вигляді добутку: а) 64; (-7)6; 1,25; а) a 5; (2 х)3; (bc)4. Знайдіть значення степеня: 239. а) 122; б) 44; в) (-0,7)3; г) (-1,5)4; д) 240. а) 25; б) (-3)4; в) (-1)5; г) 0,43; д) 1,13; е) 0,043; є) Обчисліть: 241. а) 6 × (-2)4; б) 6 × (-24); в) 5 × (-3)3; г) 5 × (-33); д) 53 - 52; е) (-6 × 0,5)5; є) 0,13 - 0,12; ж) (15 - 16)10. 242. а) (3 - 7)4; б) 2 × (-73); в) 26 + (-3)3; г) (-4 + 3)9. 243. Знайдіть значення виразу: а) а 2; (- а)2; - а 2, якщо а = 3; б) а 3; (- а)3; - а 3, якщо а = 10. 244. Знайдіть значення виразу: а) 2 а 3 + 1, якщо а = -2; а = 0; а = 2; б) (х + 1)4, якщо х = -2; х = 2.
Заповніть таблицю:
Порівняйте значення виразів: 247. а) (5 × 2)2 і 52 × 22; б) (2 + 3)3 і 23 + 33; в) 74 - 64 і 54; г) 53 + 213 і 263. 248. а) (7 - 5)2 і 72 - 52; б) (10: 2)3 і 103: 23; в) 142 + 192 і 332; г) 124 - 35 і 123 + 36. Знайдіть значення виразу: 249. b 4 + b 3 + b 2 + b + 1, якщо b = -2; b = -1; b = 0; b = 1; b = 2. 250. х 5 - х 4 + х 3 - х 2 + х, якщо х = -1; х = 0; х = 2. Подайте у вигляді квадрата або куба числа: 251. 27; 144; -125; 216; 0,125; 0,001; 252. 64; 1000; -8; 6,25; 0,008; 253. Доведіть, що вираз набуває лише додатних значень: а) а 2 + 1; б) а 10 + 5; в) (а - 2)2 + 2; г) (а + 4)4 + 0,5.
254. Знайдіть значення виразу, якщо а = 0; а = 1; а = -1: а) а + а 2 + а 3 +… + а 99 + а 100 (ця сума має 100 доданків, кожен з яких є степенем числа а; показники степенів ¾ усі натуральні числа від 1 до 100 включно); б) а + а 2 + а 3 +… + а 98 + а 99; в) аа 2 а 3… а 99 а 100; г) аа 2 а 3… а 98 а 99. 255. Знайдіть найменше значення виразу: а) а 2 + 1; б) а 4 - 2; в) (а - 1)2 + 12; г) (2 а + 2)4 - 5. Для якого значення а значення виразу є найменшим? 256. 1) Доведіть, що вираз набуває лише додатних значень: а) х 2 +(х + 1)2; б) (х - 2)2 + (х - 1)8; в) х 4 + | х + 1|. 2) Розв’яжіть рівняння: а) х 2 +(х + 1)2 = 0; б) (х - 2)2 + (х - 1)8 = 0; в) х 4 + | х + 1| = -1. 257. Знайдіть останню цифру числа 987987. Вправи для повторення
258. Розв’яжіть рівняння: а) 5 х - 3 = 3 х + 17; б) 7 х + 32 = 12 х + 25; в) 2(х - 11) - 5(5 - 2 х) = –23; г) 8(-3 х + 4) + 14(3 + 2 х) = 4 + 2 х. 259. Футбольна команда у 15 матчах набрала 23 очка, програвши 6 матчів. У скількох матчах команда здобула перемогу і скільки матчів зіграла внічию? (За перемогу команді нараховується 3 очка, за нічию ¾ 1 очко, за поразку ¾ 0 очок.) 260. Середнє арифметичне трьох чисел дорівнює -8. Перше число на 5 більше від другого, а друге — на 1 менше від третього. Знайдіть ці числа. Властивості степеня з натуральним показником
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 589; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.195.185 (0.009 с.) |

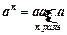 , якщо n > 1,
, якщо n > 1, Приклади розв’язання вправ
Приклади розв’язання вправ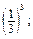
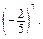
 0,12.
0,12. Рівень А
Рівень А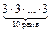 ;
;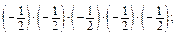 г)
г) 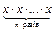 ;
;
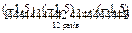 ; г) (ab) × (ab) × (ab) × (ab) × (ab).
; г) (ab) × (ab) × (ab) × (ab) × (ab). е)
е)  є)
є) 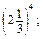 ж) (-0,02)3.
ж) (-0,02)3.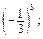 ж)
ж) 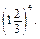
 Рівень Б
Рівень Б

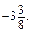

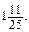
 Рівень В
Рівень В


