
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розв’язування головних геодезичних задачСодержание книги
Поиск на нашем сайте
а) на поверхні сфери
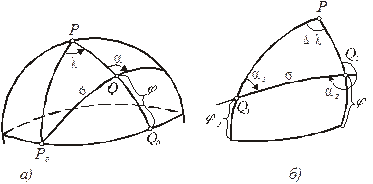
Використання сфери вигідно, в першу чергу, для наближеного розв’язування головних геодезичних задач - прямої та оберненої. Введемо наступні позначення координат на сфері (рис.3.4): j - географічна широта; l - географічна довгота; a - азимут дуги великого кола;
 ). ).
Рис.3.4
Пряма геодезична задача Нехай задані географічні координати j1, l1 деякої точки Q1 (рис. 3.4б), а також полярні координати s і a1 другої точки Q2. Вимагається за цими даними знайти географічні координати j2, l2 точки Q2 і азимут a2 з другої точки на першу. Таким чином, пряма геодезична задача полягає в перетворенні полярних координат в географічні (сферичні). Обернена геодезична задача. Нехай задані географічні координати j1, l1 і j2, l2 двох точок Q1 і Q2 (рис. 3.4б). Необхідно знайти найкоротшу відстань s (довжину дуги великого кола) між даними точками та азимути a1 і a2 з однієї точки на другу. Отже, обернена геодезична задача зводиться до перетворення географічних (сферичних) координат в полярні. Розв’язування прямої і оберненої геодезичних задач на сфері, як легко можна побачити, представляє собою розв'язування полярного сферичного трикутника Q1PQ2 (рис.3.4б). В даному випадку розв'язування цього трикутника зводиться до визначення за двома сторонами і кутом між ними третьої сторони та прилеглих до неї кутів. Для розв'язування можна використати замкнуті формули сферичної тригонометрії:
Формули для розв’язування прямої геодезичної задачі:
де
Шляхом ділення рівнянь (3.19) на (3.18) дістанемо формулу для оберненого азимута
Формули для розв’язування оберненої геодезичної задачі: Для обчислення прямого азимута треба розділити рівняння (3.12) на (3.14)
Для обчислення оберненого азимута необхідно розділити рівняння (3.13) на (3.15)
Формулу для sins отримаємо, якщо помножимо рівняння (3.12) на sina1, а рівняння (3.14) - на cosa1 і додамо їх
Обчислення арксинуса можна замінити обчисленням арктангенса, використавши формулу зв’язку, аналогічну (3.21). Із трикутника Q1 PQ2 (див. рис. 3.4.б) можна отримати і інші варіанти формул для розв’язування прямої та оберненої геодезичних задач.
б) на поверхні еліпсоїда
В практиці розв'язування головних геодезичних задач на поверхні еліпсоїда між точками 1 і 2 використовуються різноманітні лінії, що дають однозначне положення точки 2 по відношенню до точки 1. За такі лінії можна прийняти прямий нормальний переріз, геодезичну лінію, центральний переріз, хорду тощо. Використання кожної з вказаних ліній вносить свої особливості в методи розв’язування головних геодезичних задач на поверхні еліпсоїда. Ми будемо розглядати тільки ті методи, які базуються на використанні геодезичної лінії і найбільш часто зустрічаються в практиці. Раніше нами були отримані диференційні рівняння, що характеризують зміну широти і довготи при переміщені вздовж будь-якої кривої на поверхні еліпсоїда
і зміна азимуту вздовж геодезичної лінії
Ці три рівняння представляють собою систему звичайних диференційних рівнянь першого порядку, що пов’язують чотири змінних - B, L, A, s, з яких довжина геодезичної лінії s прийнята як незалежна змінна. Проінтегрувавши їх по незалежній змінній s між точками Q1 і Q2,, отримаємо
Інтеграли (3.29) не виражаються в елементарних функціях, тому для їх наближеного розв'язування застосовують розклади в ряди або підінтегральних функцій або самих інтегралів з наступним почленним інтегруванням кожного ряду. При цьому для практичного застосування можливими є два варіанти їх розв'язування. Оскільки розв'язування головних геодезичних задач на сфері виконується строго за формулами сферичної тригонометрії (див. п. 3.4.2.а), а форма земного еліпсоїда незначно відрізняється від сфери, доцільним є наступний порядок розв'язування: · обчислення за заданими елементами на еліпсоїді відповідних елементів на сфері, тобто здійснити перехід з еліпсоїда на сферу; · розв'язування головних геодезичних задач на сфері; · обчислення за елементами на сфері відповідних елементів на еліпсоїді, тобто провести зворотній перехід зі сфери на еліпсоїд. Перехід з еліпсоїда на сферу, котре ще називають геодезичним зображенням, базується на зображенні геодезичної лінії еліпсоїда на сфері у вигляді дуги великого кола, причому кожній точці геодезичної лінії відповідала б єдина точка дуги великого кола як її зображення. Така відповідність вважається встановленою, якщо знайдені математичні залежності між елементами B, L, A, s в кожній точці геодезичної лінії на еліпсоїді та елементами j, l, a, s у відповідній точці дуги великого кола на сфері. В загальному вигляді ці залежності можна записати системою наступних диференційних рівнянь:
Очевидно, що аргументами функцій fi будуть широта B, азимут A та квадрат ексцентриситета e2, як аргумент радіусів кривини M і N еліпсоїда. Проінтегрувавши диференційні рівняння (3.30) при певних умовах, можна отримати необхідні формули для взаємного переходу з еліпсоїда на сферу. Одним із найбільш відомих способів розв’язування головної геодезичної задачі вказаним вище шляхом є спосіб Бесселя. Саме такий варіант є практичним втіленням так званого прямого шляху розв’язування головних геодезичних задач. Прямий шлях полягає в безпосередньому розв’язуванні сфероїдного трикутника Q1PQ2 (див. рис.3.1) за відомими двома сторонами і кутом між ними, а саме: ¨ в прямій геодезичній задачі відомі сторони Q1P = 900-B1; Q1Q2=s і кут A1, із розв'язування трикутника визначаються інші його елементи - різниця довгот ¨ в оберненій геодезичній задачі відомі сторони Q1P, Q2P та різниця довгот Сторони Q1P і Q2 P сфероїдного трикутника Q1PQ2 можуть досягати декількох тисяч кілометрів (наприклад, при розташуванні сторони Q1Q2 на широті 500, вказані сторони будуть біля 4 000 км). Розв’язування таких значних за розмірами трикутників пов’язано з досить великими труднощами, адже при цьому немає кінцевих замкнутих формул, оскільки сторони сфероїдних трикутників, що представляють собою дуги меридіанів і паралелей та геодезичні лінії на поверхні еліпсоїда, виражаються еліптичними інтегралами. Ось чому на практиці, при розв’язуванні сфероїдних трикутників, їх спочатку проектують на допоміжну сферу, на котрій виконують розв'язування, після чого здійснюють обернений перехід на еліпсоїд. У всіх способах прямого шляху розв’язування головних геодезичних задач сферична поверхня використовується як проміжна інстанція, причому вона може бути використана і при виводі формул, і в процесі практичних обчислень. Способи, що базуються на прямому шляху, придатні для розв’язування прямих та обернених геодезичних задач на поверхні земного еліпсоїда при будь-яких віддалях між двома точками і з будь-якою практично необхідною точністю. Побічний шлях полягає у визначенні приростів (різниць) широт, довгот і азимутів у функції заданих величин, після чого за знайденими приростами визначаються остаточні величини. Так, наприклад, при розв’язуванні прямої геодезичної задачі попередньо визначаються різниці:
В правих частинах цих рівнянь через f1, f2 і f3 позначені функції, що виражаються розкладами приростів широти, довготи та азимута в ряди за степенями довжини s:
Після чого знаходять
Кількість членів розкладів утримується в залежності від довжини s: чим більша відстань, тим більше членів в рядах (3.32) при одній і тій же точності обчислень треба утримувати. Це і є розглянутий нами вище другий варіант розв'язування рівнянь (3.29), який відомий ще як непрямий або побічний шлях розв’язування головних геодезичних задач. Перші коефіцієнти цих рядів задані рівняннями (3.27) і (3.28). Інші коефіцієнти знаходять шляхом послідовного диференціювання перших коефіцієнтів за змінними B і A як складних функцій. Так, наприклад, загальний запис для похідних вищих порядків широти буде мати вигляд
Часткові похідні для другої похідної будуть наступними
Враховуючи відомі співвідношення та позначення (див. розділ 2):
отримаємо
звідки
Часткова похідна
З врахуванням отриманих виразів та формули (3.28) остаточно отримаємо
Аналогічним чином можна отримати і вирази для похідних вищих порядків. Приведемо без виводу вирази для похідних широти до п’ятого порядку включно
Вирази для похідних шостого і вище порядків мають досить складний вид і мало перспектив на їх застосування в практичних обчисленнях. Приведемо ще вирази для аналогічних похідних довготи та азимута
У виразах для похідних п’ятого порядку (3.34), (3.35), (3.36) знехтувано стисненням еліпсоїда (h=0) та прийнято, що M=N=R, де R - середній радіус еліпсоїда (земної кулі; можна прийняти R=a). Практичні розрахунки показують, що з врахуванням похідних до третього порядку можна розв’язувати пряму геодезичну задачу на відстані до 40 км з точністю 0.0002” в широті та довготі і 0.001” в азимуті, а з врахуванням наведених похідних до п’ятого порядку і до 100 км з такою ж точністю. Обчислення за цими формулами при “ручних” рахунках були надзвичайно громіздкими, тому застосовувались певні раціональні прийоми, що дозволяли перетворювати формули для їх широкого практичного застосування. Вкажемо лише на два з них, що мали широке практичне використання при опрацюванні геодезичних мереж 1-го класу: метод допоміжної точки Шрейбера та метод середніх аргументів Гаусса. В зв’язку з широким впровадженням комп’ютерної техніки на даний час можна вважати, що найбільш оптимальним шляхом розв’язування головних геодезичних задач є використання чисельних методів інтегрування диференційних рівнянь (3.27) і (3.28). Одним із найефективніших чисельних методів для вказаної задачі є метод Рунге-Кутта четвертого порядку. Детальніше про цей шлях буде розглянуто в п.3.6.4.
в) в просторі
Для розв’язування головних геодезичних задач в просторі використовують системи просторових декартових (X, Y, Z), геодезичних (B, L, H) та топоцентричних горизонтальних - декартових (x’, y’,z’) та полярних (A, z, D) координат і зв’язки між ними (див. розділи 1 і 2). Пряма геодезична задача формулюється наступним чином. Задані геодезичні координати B1,L1,H1 початкової точки Q1 і топоцентричні полярні координати z12, A12, D точки Q2 відносно початкової точки Q1. Необхідно визначити геодезичні координати B2,L2,H2 точки Q2. Поставлену задачу розв’язують в такій послідовності: а) за формулами зв’язку (2.32) обчислюють просторові декартові координати X1,Y1,Z1 точки Q1; б) обчислюють елементи матриці перетворення координат A1 за формулою (2.37). в) використовуючи формули (2.34), обчислюють топоцентричні декартові координати x2’,y2’,z2’; г) за формулою (2.36) обчислюють декартові координати X2,Y2,Z2 точки Q2; д) для переходу до геодезичних координат B2,L2,H2 точки Q2 використовують формули зв’язку (2.33). Обернена геодезична задача. Задані геодезичні координати B,L,H двох точок Q1 та Q2. Необхідно знайти топоцентричні полярні координати z12, A12, D точки Q2 відносно початкової точки Q1. Для розв’язування поставленої задачі можна застосувати таку схему: а) від геодезичних координат B,L,H точок Q1 та Q2 за формулами (2.32) переходять до декартових Xi,Yi,Zi (де і=1,2); б) обчислюють елементи транспонованої матриці перетворення координат
в) за формулою (2.38) обчислюють топоцентричні декартові координати xi’,yi’,zi’ (і=1,2) точки Q1 відносно точки Q2 і навпаки. г) топоцентричні полярні координати z12, A12, D точки Q2 відносно початкової точки Q1 і z21, A21, D точки Q1 відносно точки Q2 обчислюють за формулами (2.35). Приведені вище схеми можна використовувати також і для розв’язування головної геодезичної задачі між точками на поверхні еліпсоїда. Для цього в цих формулах достатньо прийняти H1=H2= 0. Розв’язком при цьому, наприклад, в оберненій геодезичній задачі будуть азимути прямого і оберненого нормальних перерізів та довжина хорди цих перерізів.
Диференційні формули
Диференційні формули встановлюють залежність між малими (диференційними) змінами координат початкової і кінцевої точок відповідної лінії (дуги великого кола на сфері, геодезичної лінії на еліпсоїді, хорди в просторі), її довжини та азимутів. Застосування диференційних формул пов’язано, в основному, з розв’язуванням задач з переобчислення геодезичних координат на поверхні земного еліпсоїда чи геоцентричних прямокутних в просторі у випадках зміни вихідних координат, а також аналогічних задач у випадку зміни (уточнення) розмірів відлікового еліпсоїда. Особливо це може стосуватися задач, що виникають при поєднанні пунктів, координати яких віднесені до референцних та загальноземного еліпсоїдів та визначені різними методами (класичними і супутниковими, наприклад). Диференційні формули дозволяють значно скоротити обчислювальну роботу, яка вимагається при подібному переобчисленні вже врівноважених координат всіх опорних геодезичних пунктів. Це виявляється можливим тому, що повторне обчислення координат замінюється обчисленням незначних поправок до вже відомих координат пунктів. Такими формулами для обчислення поправок в координати та азимути напрямів і є диференційні формули. Крім вищеназваних, диференційні формули можна використовувати і в інших задачах. Так в п. 3.6. буде наведена схема розв’язування оберненої геодезичної задачі, одним із важливих етапів якої є застосування диференційних формул для довжини геодезичної лінії та азимута цієї лінії.
|
||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 1238; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.92.213 (0.008 с.) |

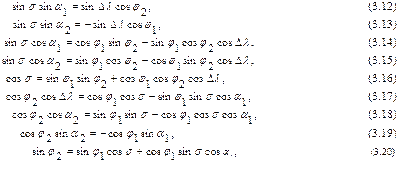
 (3.21)
(3.21)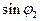 визначається за формулою (3.20). Різниця довгот Dl знайдеться, якщо розділити рівняння (3.12) на (3.17)
визначається за формулою (3.20). Різниця довгот Dl знайдеться, якщо розділити рівняння (3.12) на (3.17)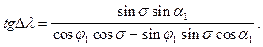 (3.22)
(3.22)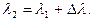
 (3.23)
(3.23)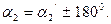
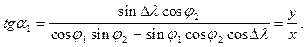 (3.24)
(3.24)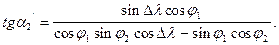 (3.25)
(3.25) (3.26)
(3.26)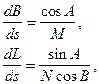 (3.27)
(3.27)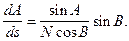 (3.28)
(3.28)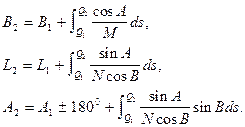 (3.29)
(3.29)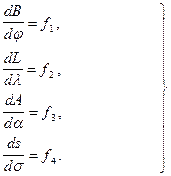 (3.30)
(3.30) , котра служить для визначення геодезичної довготи L2, сторона Q2P = 900 - B2 і кут A2’ (A2 = 3600 - A2’);
, котра служить для визначення геодезичної довготи L2, сторона Q2P = 900 - B2 і кут A2’ (A2 = 3600 - A2’);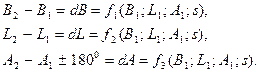 (3.31)
(3.31)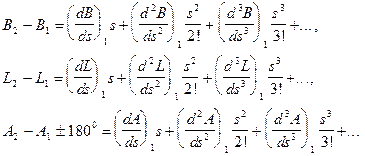 (3.32)
(3.32)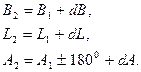 (3.33)
(3.33)

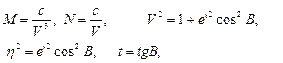
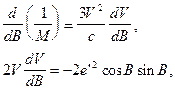
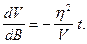

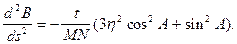
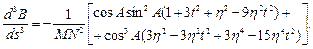
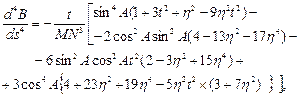
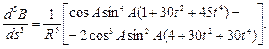 (3.34)
(3.34)


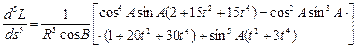 .(3.35)
.(3.35)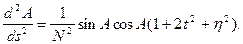
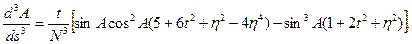
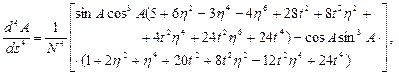
 (3.36)
(3.36)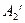 за формулою
за формулою



