
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Диференційні формули для системи геодезичних координатСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Зміна розмірів еліпсоїда і його орієнтування відносно фізичної поверхні Землі викликає зміну геодезичних координат всіх точок навколишнього простору. Формули, за якими визначаються малі зміни геодезичних координат B, L, H точок земної поверхні або навколоземного простору, що викликані малими змінами розмірів еліпсоїда і його паралельним зсувом в просторі носять назву диференційних формул системи геодезичних координат. Нехай деякий еліпсоїд заданих розмірів (a, a) встановлений відносно земної поверхні так, що вісь обертання його паралельна до осі обертання Землі, а центр еліпсоїда незначно віддалений від центра інерції Землі. Якщо тепер змінимо форму і розміри еліпсоїда: велику (екваторіальну) піввісь на величину da, а стиснення на величину da, то, відповідно, зміняться при цьому і геодезичні координати B,L,H всіх точок простору, проте прямокутні координати X,Y,Z цих точок залишаться попередніми, поскільки не змінилося положення осей координат. Здійснивши паралельне зміщення еліпсоїда в просторі разом з осями координат OXYZ, отримаємо додаткові зміни геодезичних координат. Зміняться на цей раз і прямокутні координати всіх точок (в результаті переносу початку координат) на величини dx, dy, dz. Вказані зміщення (перехід від одної системи геодезичних координат до другої) можна проілюструвати геометрично (рис. 3.6). В загальному вигляді залежності між всіма вказаними змінами можна записати у вигляді системи диференційних рівнянь
Рис.3.6
Диференціали da, da та dB, dL, dH, dx,dy,dz представляють собою поправки до старих значень розмірів еліпсоїда (a,a) і координат (B,L,H,X,Y,Z) довільної точки простору для отримання нових значень цих величин в другій системі геодезичних координат. Часткові похідні в рівняннях (3.49) знаходимо шляхом диференціювання по відповідних змінних правих частин рівнянь (3.43). Раніше (див. п.3.5.2) нами вже отримано частину похідних (3.46). Аналогічним чином знаходять і інші похідні в (3.49). Підставивши ці похідні в рівняння (3.49) та після відповідних перетворень, отримаємо остаточно
Умовою застосування вказаних диференційних формул є паралельність осей обертання та площин початкових меридіанів обох еліпсоїдів. Отримані вище формули можуть використовуватись: · для обчислення поправок в координати при переході до другої системи геодезичних координат (при відомих параметрах da, da, dx,dy,dz); · для встановлення нової системи геодезичних координат (визначення вказаних п’яти невідомих параметрів). Поправки da, da легко знайти, поскільки параметри еліпсоїдів, що застосовуються в практичних роботах, переважно відомі. Що стосується інших трьох поправок, то вони визначаються наступним чином. За геодезичними координатами декількох пунктів Qi (i=1,2,...,n), відомими в двох системах координат, з допомогою формул (3.50-3.52) можна визначити лінійний зсув dx,dy,dz одної системи відліку геодезичних координат відносно другої. Вказану задачу можна сформулювати ще так. Дано координати окремих пунктів геодезичної мережі - (X,Y,Z), визначених з допомогою GPS в системі WGS-84. Обчислити параметри перетворення для геодезичної мережі, у якій більшість пунктів є з відомими координатами B,L,H в системі деякого референцного еліпсоїда, причому деякі з них є спільними (відомі координати в обох системах відліку). Розв'язування цієї задачі дістанемо за допомогою наступного алгоритму: · для спільних пунктів виконуємо перетворення декартових X,Y,Z, заданих в системі WGS-84 вгеодезичні B,L,H координати за допомогою формул (2.33)); · визначаємо три параметри перетворення dx,dy,dz на основі формул (3.50-3.52); · для пунктів GPS, які не належать до спільних, використовуючи параметри перетворення, знаходимо координати (B,L,H)REF в системі референцного еліпсоїда; Нехай референцна система XYZ визначена в іншій системі X0Y0Z0 положенням початку координат dx,dy,dz і кутами ex, ey, ez, на які треба повернути систему XYZ відповідно навколо осей X, Y, Z, щоб ці осі стали паралельні відповідно осям X0,Y0, Z0. В такій постановці декартові координати із одної системи в іншу будуть перетворюватись за формулами:
При невеликих кутах повороту осей однієї системи координат відносно другої, що має місце в практиці, матриця перетворення R має елементи
У формулі (3.54) R’ - транспонована матриця R, m - масштабний множник. Для більшості задач, що виникають при переобчислені координат сучасних систем координат можна вважати, що m=1. Перетворення (3.54) називається ще перетворенням або трансформацією Гельмерта. Формулу (3.54) можна представити і в такому виді:
Кожен пункт Qi (i=1,2,...,n), координати якого відомі в двох системах координат, утворює систему рівнянь (3.55). Шукані параметри зв’язку двох систем координат можна обчислити з оцінкою точності, застосовуючи принцип найменших квадратів. Розв'язування сформульованої вище задачі зв’язку двох систем координат дістанемо за допомогою наступного алгоритму: 1) для спільних пунктів виконуємо перетворення геодезичних координат B,L,H в декартові X,Y,Z за допомогою формул (2.32); 2) визначаємо шість параметрів перетворення dx,dy,dz і 3) для пунктів загальноземної системи координат, які не належать до спільних, використовуючи параметри перетворення, знаходимо координати (X,Y,Z)REF в референцній системі; 4) перетворюємо обчислені в попередньому кроці координати із декартових (X,Y,Z)REF в геодезичні (B,L,H)REF. Точність переобчислених координат буде залежати: · від похибок формул, що застосовуються при обчисленнях; · від методів переходу виміряних елементів геодезичних мереж на поверхню референц-еліпсоїда; від врівноважень, виконаних в геодезичних мережах кожної системи незалежно одна від другої.
|
||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 521; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.007 с.) |

 (3.49)
(3.49)
 (3.50)
(3.50)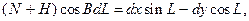 (3.51)
(3.51)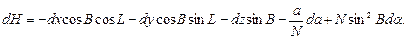 (3.52)
(3.52) (3.53)
(3.53)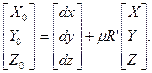 (3.54)
(3.54)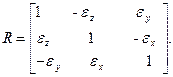 (3.55)
(3.55)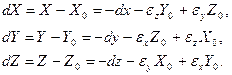 (3.55)
(3.55)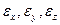 на основі формул (3.54) або (3.55).
на основі формул (3.54) або (3.55).


