
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методи розв’язування головних геодезичних задач на поверхні еліпсоїдаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
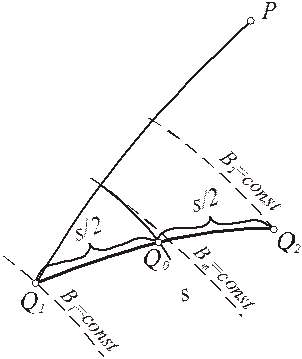
3.6.1. Розв’язування головних геодезичних задач методом із середніми аргументами (формули Гаусса) Пряма геодезична задача Нехай на рис.3.7 крива Q1Q2 є геодезичною лінією між початковою точкою Q1 і кінцевою Q2.
Рис. 3.7
Візьмемо точку Qo, розташовану на середині геодезичної лінії Q1Q2. Застосувавши формули (3.32) до кожної частини геодезичної лінії, отримаємо для широти
Віднявши в (3.56) перше рівняння від другого знаходимо
Для різниць довгот та азимутів отримаємо аналогічно:
Залежності між цими координатами можна отримати, якщо додати рівняння (3.56) і поділити на два:
Аналогічно
Як видно, ці залежності – малі величини другого порядку. Приведені вище формули в загальному виді розв’язують поставлену задачу. Але оскільки ставиться за мету отримати різниці координат у функції Bm і Am, то потрібно встановити залежність між вказаними похідними. Вона виражається з допомогою ряда Тейлора:
Часткові похідні, що входять в дану формулу дорівнюють:
З похибкою на малі величини четвертого порядку, остаточно отримаємо
а з похибкою на величину третього порядку можна записати:
Використавши вирази (3.59) для перетворення поправочних членів у формулі (3.58) і не приймаючи до уваги члени
Для різниці довгот та азимутів формули отримуються аналогічним чином. Запишемо ці формули в кінцевому виді
Наведені скорочені формули для різниць широт, довгот та азимутів відрізняються від повних формул типу (3.58), які точні до величин четвертого порядку включно, лише на відкинуті малі величини порядку В формулах (3.60)-(3.62) величини b,l,a – функції середньої широти Bm і середнього азимута Am, які невідомі. Невідомі також і аргументи b і l в поправочних членах вказаних формул. Тому пряма геодезична задача розвязується методом послідовних наближень наступним чином.
Приймаємо b і a рівними нулю, тобто
і з цими значеннями обчислюємо в першому наближенні bІ,lІ,aІ, а потім знаходимо
З цими наближеними значеннями знаходимо нові, більш точні значення Bm і Am та повторюємо обчислення b і a, а також l. Так поступають до тих пір, поки результати обчислень із двох суміжних наближень не стануть одинаковими.
Обернена геодезична задача. При відомих значеннях
Для знаходження невідомих
Для знаходження Am представимо формули (3.60) та (3.61) у виді
Розділивши ці два рівняння, отримаємо
Величину
Довжину геодезичної лінії
3.6.2. Розв’язування прямої геодезичної задачі методом допоміжної точки (формули Шрейбера)
Нехай на рис.3.8 PQ1Q2 – сфероїдний полярний трикутник, який потрібно розвязати за такими даними: широтою B1 і довготою L1, довжиною s геодезичної лінії, що з'єднує точки Q1 i Q2, а також азимутом A1 цієї лінії в точці Q1 (прямий азимут).
Рис. 3.8
Розділимо трикутник Вивід формул Шрейбера буде складатись із наступних етапів. Із прямокутного сфероїдного трикутника Q1С Q2 за даними A1 і s визначають катети x і y, використовуючи теорему Лежандра та сферичний надлишок цього трикутника. На рис. 3.8.б представлений трикутник Q1’Q2’C’, який відповідає сфероїдному трикутнику Q1 С Q2. Застосовуючи формули розкладу в ряд (3.32) можна розв’язати пряму геодезичну задачу для точок Q1 і С. Поскільки для цієї пари точок A1=0 і s=x, то все зводиться тільки до визначення різниці широт b. За тими ж формулами розв’язують пряму геодезичну задачу з точки С, широта якої
Отже, замість прямого застосування рядів (3.32) до точок Q1 і Q2 їх застосовують послідовно до точок Q1 і С, а потім до точок С і Q2, тобто у випадках, коли A=0o і A=90o. В результаті отримаємо: Сума всіх кутів навколо точки Q2 дасть
звідки
Розглянемо детальніше вивід основних формул. Із плоского трикутника Q1’С’Q2’, використовуючи теорему Лежандра, за формулою синусів отримаємо
де сферичний надлишок може бути достатньо точно обчислений за формулою
Для визначення широти Bo, використаємо першу формулу системи (3.32), в якій при підстановці похідних (до третього порядку) врахуємо, що
Аналогічно поступають і при визначенні широти B2, тільки в цьому випадку вже
Застосуємо тепер другу і третю формули системи (3.32) для визначення приростів довготи l та азимута a відповідно. При цьому враховуємо, що
Відповідно
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 606; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.97.217 (0.008 с.) |

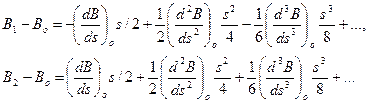 (3.56)
(3.56)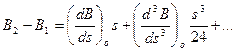
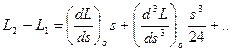

 (3.57)
(3.57) .
.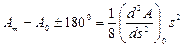 .
. .
.
 (3.58)
(3.58) (3.59)
(3.59) і менше, отримаємо для різниці широт остаточно:
і менше, отримаємо для різниці широт остаточно: (3.60)
(3.60) (3.61)
(3.61) (3.62)
(3.62)
 (3.63)
(3.63) ми можемо зразу знайти
ми можемо зразу знайти
 використовують отримані вище формули для прямої геодезичної задачі. При цьому для обчислення
використовують отримані вище формули для прямої геодезичної задачі. При цьому для обчислення  достатньо знайти
достатньо знайти  та
та  . Тоді отримаємо
. Тоді отримаємо
 (3.64)
(3.64) (3.65)
(3.65) знаходимо на основі формули (3.62)
знаходимо на основі формули (3.62) (3.66)
(3.66)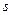 легко знаходимо із рівнянь (3.64)
легко знаходимо із рівнянь (3.64) (3.67)
(3.67)
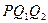 (рис.3.8.а) на два сфероїдних прямокутних трикутника геодезичною лінією Q2С, яка перпендикулярна меридіану PQ1 початкової точки. Широту точки С позначимо через
(рис.3.8.а) на два сфероїдних прямокутних трикутника геодезичною лінією Q2С, яка перпендикулярна меридіану PQ1 початкової точки. Широту точки С позначимо через 
 , а різницю широт
, а різницю широт  - через d.
- через d. та
та  .
. ,
, . (3.68)
. (3.68) (3.69)
(3.69)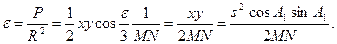 (3.70)
(3.70) :
: . (3.71)
. (3.71) :
: . (3.72)
. (3.72) (3.73)
(3.73) (3.74)
(3.74)


