
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сходимость сеточного метода решения краевых задач для обыкновенных диф. уравнений.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Для граничной задачи Лемма. Пусть выполняются условия:1) Построим посл-ть zi. Рассм. граничную задачу: E(a)=0,E(b)=0 (13) При a<x<b решение E(x) этой задачи положительно: E(x)>0. Докажем это от противного. Пусть существует такое
Методы прогонки и пристрелки решения разностных схем при решении краевых задач для обыкновенных д.у. Для гран. задачи Метод разностной прогонки. Уравнение
тут
Эквивалентность граничных и вариационных задач Рассмотрим граничную задачу
Считаем, что Задача (1),(2) поставим в соответствующую вариационную задачу На множестве Теорема. Пусть Док- во Если
Теорема Пусть Док-во. Положим Рассмотрим первое слагаемое второго интеграла в первой части равенства (5), интегрируем по частям имеем: С учетом этого равенства и того, что
В силу условий наложенных на функции
|
||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 577; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

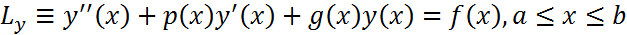 , (1) y(a)=A, y(b)=B (2) на равномерной сетке xi=a+ih, i=0,1,...,N;h=(b-a)/N построена разностная схема
, (1) y(a)=A, y(b)=B (2) на равномерной сетке xi=a+ih, i=0,1,...,N;h=(b-a)/N построена разностная схема  , (3) y0=A, yN=B (4). Точное решение y(x) в узлах сетки:
, (3) y0=A, yN=B (4). Точное решение y(x) в узлах сетки:  , (5)
, (5)  , y(xN)=B (6). Для погрешности, с которой алгебраические уравнения (3) приближают диф-ое уравнение (1) в узлах сетки, была получена оценка
, y(xN)=B (6). Для погрешности, с которой алгебраические уравнения (3) приближают диф-ое уравнение (1) в узлах сетки, была получена оценка  (7). Граничные условия приближаются точно. Фактическое решение
(7). Граничные условия приближаются точно. Фактическое решение  системы (3), (4), вследствие выч-ой погрешности, отличается от точного решения yi этой системы, =>
системы (3), (4), вследствие выч-ой погрешности, отличается от точного решения yi этой системы, => 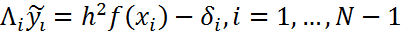 , (8)
, (8) 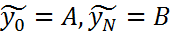 (9) Оценим погрешности
(9) Оценим погрешности  . Вычитая из (5), (6) соотв. ур-ния (8), (9), получим разностную задачу
. Вычитая из (5), (6) соотв. ур-ния (8), (9), получим разностную задачу  , (10)
, (10)  (11).
(11). 2) g(x)≤0,a≤x≤b 3)
2) g(x)≤0,a≤x≤b 3) 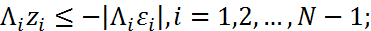 4)
4)  , для произвольных последовательностей
, для произвольных последовательностей  ,
, 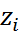 .Тогда
.Тогда  , i=0,1,...N. Док-во. Рассмотрим 2 числовые последовательности zi±εi, i=0,1,...,N. Из условия 3) леммы имеем
, i=0,1,...N. Док-во. Рассмотрим 2 числовые последовательности zi±εi, i=0,1,...,N. Из условия 3) леммы имеем  , i=1,2...N-1. В силу принципа max для оператора
, i=1,2...N-1. В силу принципа max для оператора  последоват-ти zi±εi,i=0,1,...N принимают свое наименьшее отрицательное значение на границе. Из условия (4) на границе имеем z0±ε0≥0 и zN±εN≥0. Т.о. zi±εi≥0, i=0,1,...N лемма доказана.
последоват-ти zi±εi,i=0,1,...N принимают свое наименьшее отрицательное значение на границе. Из условия (4) на границе имеем z0±ε0≥0 и zN±εN≥0. Т.о. zi±εi≥0, i=0,1,...N лемма доказана. ,(12)
,(12)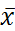 , что
, что  и
и  . Тогда внутри отрезка найдется точка
. Тогда внутри отрезка найдется точка  , в которой достигается неположит-ый min:
, в которой достигается неположит-ый min: 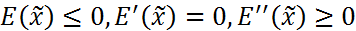 . В результате противоречие
. В результате противоречие  . Для последов-ти
. Для последов-ти  выполняются условия 4) леммы сравнения при любой положительной константе C. Найдем значение константы C, при котором будут выполнены условия 3). Из (10) и (7) имеем
выполняются условия 4) леммы сравнения при любой положительной константе C. Найдем значение константы C, при котором будут выполнены условия 3). Из (10) и (7) имеем  , или
, или  (14), где
(14), где 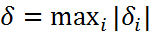 ,
,  ,
, 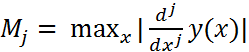 ,
,  . Из
. Из  получим при достаточно малом h
получим при достаточно малом h  ,
,  ,(15), где
,(15), где  ,
,  . Из (14) и (15) следует, что для вып. усл. 3) леммы сравн. полож. константы C должно удовлетворять неравенству
. Из (14) и (15) следует, что для вып. усл. 3) леммы сравн. полож. константы C должно удовлетворять неравенству  . => получ.
. => получ.  .Использ. лемму сравнения, приходим к искомой оценке
.Использ. лемму сравнения, приходим к искомой оценке  (16) Из оценки (16) вытекает, что решение
(16) Из оценки (16) вытекает, что решение  на равномерной сетке
на равномерной сетке  была построена разностная схема
была построена разностная схема  . Коэффициенты в уpавнениях (3):
. Коэффициенты в уpавнениях (3):  (5). Метод разностной пристрелки. (3) можно решить относительно
(5). Метод разностной пристрелки. (3) можно решить относительно 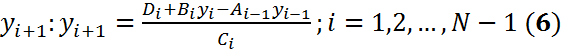 Так как
Так как 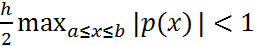 , то
, то  )>0 и операция деления в (6) реализуется. Последовательность, образуемая по правилу (6) однозначно определяется значениями первых двух своих членов:
)>0 и операция деления в (6) реализуется. Последовательность, образуемая по правилу (6) однозначно определяется значениями первых двух своих членов:  Постpоим последоват-ти
Постpоим последоват-ти  взяв в (6)
взяв в (6)  Очевидно, последоват-ть
Очевидно, последоват-ть  ,i=0,1…N
,i=0,1…N  (7) при любом значении паpаметpа σ удовлетворяет сис-ме (3) и левому граничному условию
(7) при любом значении паpаметpа σ удовлетворяет сис-ме (3) и левому граничному условию  . Чтобы выполнялось пpавое гpаничное условие
. Чтобы выполнялось пpавое гpаничное условие  , нужно взять
, нужно взять  (8)
(8) Пусть мы выpазили
Пусть мы выpазили  через
через  фоpмулой
фоpмулой  Подставим это для
Подставим это для  -
-  . Отсюда находим
. Отсюда находим  Т.о. коэффициенты в (9)
Т.о. коэффициенты в (9)  После этого из (9) пpи i=N имеем
После этого из (9) пpи i=N имеем  . По фоpмуле (9) пpи i=N,N-1…2 последовательно вычисляем
. По фоpмуле (9) пpи i=N,N-1…2 последовательно вычисляем  . Гpаничные значения
. Гpаничные значения  даны. Данный метод решения граничной задачи - метод пpогонки. Вычисления по (10) - прямой ход прогонки, а по (9) – обратный. Теорема. В расчетных формулах (10) знаменатели не обращаются в нуль. Доказательство. Задано
даны. Данный метод решения граничной задачи - метод пpогонки. Вычисления по (10) - прямой ход прогонки, а по (9) – обратный. Теорема. В расчетных формулах (10) знаменатели не обращаются в нуль. Доказательство. Задано 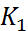 =0. Пусть
=0. Пусть  <1, тогда |
<1, тогда | 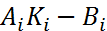 |=
|=  . Далее
. Далее  =|
=|  |<1. Утверждение теоремы доказано. Т.к.
|<1. Утверждение теоремы доказано. Т.к. 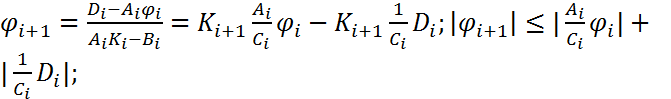

 ;
;

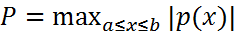 . Учитывая
. Учитывая 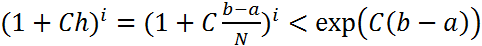 при 0≤i≤N оценка
при 0≤i≤N оценка  Т.о. на прямом ходе прогонки по (10) при
Т.о. на прямом ходе прогонки по (10) при  ограниченые, =>устойчивы к вычислительной погрешности.
ограниченые, =>устойчивы к вычислительной погрешности. ,
,  (1)
(1)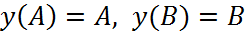 (2)
(2)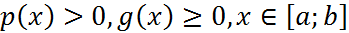 при данных предположениях существует единственное решение задач (1),(2) класса
при данных предположениях существует единственное решение задач (1),(2) класса 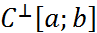 .
. (3)
(3) (4)
(4) решение вариационной задачи (3),(4), тогда
решение вариационной задачи (3),(4), тогда  функция доставляет
функция доставляет 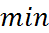 функционалу
функционалу  , то она необходимо удовлет-воряет условию Эйлера
, то она необходимо удовлет-воряет условию Эйлера  . В данном случае это уравнение будет иметь вид:
. В данном случае это уравнение будет иметь вид:
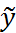 решение задачи (1),(2), тогда на функции
решение задачи (1),(2), тогда на функции  принимает минимальное решение и кроме того
принимает минимальное решение и кроме того  , где
, где  такова что
такова что 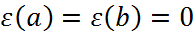 , тогда
, тогда  (5)
(5)
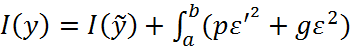 (6)
(6)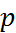 и
и  интеграл
интеграл  , поэтому из (6) следует, что на функцию
, поэтому из (6) следует, что на функцию  , то
, то 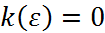 , а значит
, а значит  , поскольку
, поскольку  , то
, то  .
.


