Источники и классификация погрешностей. Неустранимая и вычислительная погрешность.
Постановка задачи интерполирования. Существование и единственность обобщенного интерполяционного многочлена.
Интерполирование или интерполяция – это один из наиболее часто применяемых на практике методов приближения функций. Задача интерполирования ставится следующим образом.
Рассмотрим пространство  функций, определенных на отрезке функций, определенных на отрезке  . Пусть в пространстве . Пусть в пространстве  задана последовательность линейно независимых функций задана последовательность линейно независимых функций  . Пусть также на отрезке . Пусть также на отрезке  задана последовательность попарно неравных точек задана последовательность попарно неравных точек  при при  . Образуем линейную комбинацию . Образуем линейную комбинацию  (1) (1)
Линейную комбинацию вида (1) называют обобщенным многочленом по системе функций  . .
Систему функций  называют системой Чебышева на отрезке называют системой Чебышева на отрезке  , если любой нетривиальный обобщенный многочлен по этой системе обращается в нуль на отрезке , если любой нетривиальный обобщенный многочлен по этой системе обращается в нуль на отрезке  не более чем в n точках. не более чем в n точках.
В задаче интерполирования функцию  нужно приблизить обобщенным многочленом (1) так, чтобы значения функции и обобщенного многочлена совпадали в заданных точках: нужно приблизить обобщенным многочленом (1) так, чтобы значения функции и обобщенного многочлена совпадали в заданных точках:
 . (2) . (2)
Обобщенный многочлен  , удовлетворяющий условиям (2), называют интерполяционным обобщенным многочленом. При этом функцию , удовлетворяющий условиям (2), называют интерполяционным обобщенным многочленом. При этом функцию  , для которой строится интерполяционный обобщенный многочлен, называют интерполируемой функцией, а точки , для которой строится интерполяционный обобщенный многочлен, называют интерполируемой функцией, а точки  называют узлами интерполяции. Равенства (2) будем называть интерполяционными условиями. называют узлами интерполяции. Равенства (2) будем называть интерполяционными условиями.
Теорема существования и единственности интерполяционного обобщенного многочлена. Для того чтобы для любой функции  при любых наборах попарно неравных узлов при любых наборах попарно неравных узлов   существовал интерполяционный обобщенный многочлен по системе функций существовал интерполяционный обобщенный многочлен по системе функций  , необходимо и достаточно, чтобы эта система функций была системой Чебышева на отрезке , необходимо и достаточно, чтобы эта система функций была системой Чебышева на отрезке  . При этом интерполяционный обобщенный многочлен будет единственным. . При этом интерполяционный обобщенный многочлен будет единственным.
Доказательство. Возьмём из (1) интерполяционные условия     (1) (1)
Интерполяционные условия представляют собой систему линейных алгебраических уравнений относительно неизвестных коэффициентов   . Система (1) имеет решение при любых правых частях тогда и только тогда, когда ее определитель . Система (1) имеет решение при любых правых частях тогда и только тогда, когда ее определитель  отличен от нуля. отличен от нуля.
Докажем необходимость. Допустим противное:  при любых наборах попарно неравных узлов на отрезке при любых наборах попарно неравных узлов на отрезке  , а система функций , а система функций  не является системой Чебышева на этом отрезке. Тогда существует нетривиальный обобщенный многочлен не является системой Чебышева на этом отрезке. Тогда существует нетривиальный обобщенный многочлен   , который обращается в нуль на , который обращается в нуль на  более чем в n точках. Возьмем n+ 1 из них в качестве узлов более чем в n точках. Возьмем n+ 1 из них в качестве узлов   . Следовательно, . Следовательно,  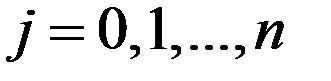 . Это означает, что столбцы определителя . Это означает, что столбцы определителя  линейно зависимы и линейно зависимы и  . Полученное противоречие доказывает необходимость. . Полученное противоречие доказывает необходимость.
Достаточность. Допустим противное: система функций  является системой Чебышева на отрезке является системой Чебышева на отрезке  , а , а 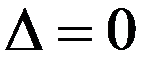 при некотором наборе попарно неравных узлов при некотором наборе попарно неравных узлов   на этом отрезке. Следовательно, столбцы определителя линейно зависимы: на этом отрезке. Следовательно, столбцы определителя линейно зависимы: 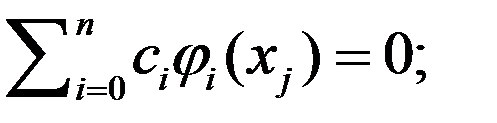  . Последнее означает, что нетривиальный обобщенный многочлен . Последнее означает, что нетривиальный обобщенный многочлен  обращается в нуль на обращается в нуль на  более, чем в n точках, то есть, система функций более, чем в n точках, то есть, система функций  не является на этом отрезке системой Чебышева. Полученное противоречие доказывает достаточность. не является на этом отрезке системой Чебышева. Полученное противоречие доказывает достаточность.
Поскольку при  система (1) имеет единственное решение, то интерполяционный обобщенный многочлен также будет при этом единственным. Теорема доказана. система (1) имеет единственное решение, то интерполяционный обобщенный многочлен также будет при этом единственным. Теорема доказана.
Интерполяционный многочлен Лагранжа.
Запишем решение с-мы   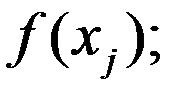  (1) по ф-лам Крамера и выполним разложение (1) по ф-лам Крамера и выполним разложение 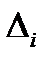 по столбцу i: по столбцу i:  . Т.о., инт. об. мн-н м. представить в виде (2) . Т.о., инт. об. мн-н м. представить в виде (2)
     .Интерполяционный многочлен Лагранжа. С-ма ф-ций .Интерполяционный многочлен Лагранжа. С-ма ф-ций  , (1) в силу осн. теоремы алгебры, явл. с-мой Чебышева на любом отрезке. Для любой ф-ции , (1) в силу осн. теоремы алгебры, явл. с-мой Чебышева на любом отрезке. Для любой ф-ции  по этой с-ме ф-ий при любом наборе попарно неравных узлов по этой с-ме ф-ий при любом наборе попарно неравных узлов   ! инт. обоб. мн-н, к-ый м. б. записан в виде ! инт. обоб. мн-н, к-ый м. б. записан в виде  , (2) где обоб. мн-ны , (2) где обоб. мн-ны  не зависят от ф-ии не зависят от ф-ии  .Зафикс. j и рассм. ф-ию .Зафикс. j и рассм. ф-ию  , приним. в узлах значения , приним. в узлах значения  Для этой ф-ии имеем инт. обоб. мн-н Для этой ф-ии имеем инт. обоб. мн-н  . Т.к. вып-ся инт. усл-я, то . Т.к. вып-ся инт. усл-я, то  . Т.о., для обоб. мн-нов . Т.о., для обоб. мн-нов  имеет место св-во имеет место св-во  (3) Если построить обоб. мн-ны (3) Если построить обоб. мн-ны  , удовл. св-ву (3), то тем самым б. построен инт. обоб. мн-н (2). Для с-мы ф-ий , удовл. св-ву (3), то тем самым б. построен инт. обоб. мн-н (2). Для с-мы ф-ий   (1),очевидно, мн-ны (1),очевидно, мн-ны  обл. св-м (3). Т.о., по с-ме ф-ий (3) инт-ый мн-н получается в виде обл. св-м (3). Т.о., по с-ме ф-ий (3) инт-ый мн-н получается в виде  (4). (4) наз. инт.мн-м Лагранжа для ф-и (4). (4) наз. инт.мн-м Лагранжа для ф-и  по по  . Обозн. . Обозн.  .имеем .имеем   и и  .С исп-ем мн-на .С исп-ем мн-на  инт.мн-н Лагранжа примет вид инт.мн-н Лагранжа примет вид  . (4’) . (4’)
Схема Эйткина
Рассм. задачу инт-ия. Ф-я  задана на задана на 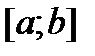 табл табл  .(1) Треб. для заданного знач. .(1) Треб. для заданного знач.  вычисл. приближ. знач. ф-и, исп-я инт. мн-н. Обозн. через вычисл. приближ. знач. ф-и, исп-я инт. мн-н. Обозн. через 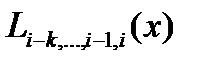 инт. мн-н, постр. для ф-и инт. мн-н, постр. для ф-и  по узлам по узлам  В сх. Эйткена сначала для заданного знач. арг. В сх. Эйткена сначала для заданного знач. арг.  выб-ся ближ-й табл. узел среди всех табл-х узлов выб-ся ближ-й табл. узел среди всех табл-х узлов  . Пусть это б. табл. узел . Пусть это б. табл. узел  . Этот табл.узел берется в кач-ве узла инт-ии . Этот табл.узел берется в кач-ве узла инт-ии  . Соотв.табл. зн-е ф-и . Соотв.табл. зн-е ф-и  обозн.через обозн.через 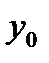 . Это табл.знач. м. сч. нач. приближением к иском. зн-ю ф-и в т. . Это табл.знач. м. сч. нач. приближением к иском. зн-ю ф-и в т.  .Далее из ост. табл. узлов .Далее из ост. табл. узлов  выбирается ближ. к выбирается ближ. к  . Это б. или . Это б. или  или или  Найденный ближ. узел обозн. Найденный ближ. узел обозн.  ,а соотв. табл. зн-е обозн. ,а соотв. табл. зн-е обозн.  Затем проводятся выч-я по ф-ле Затем проводятся выч-я по ф-ле  .(2) Здесь в числителе дроби нах. определитель кв.матрицы 2-го порядка. Опр-мый ф-ой (2) мн-н .(2) Здесь в числителе дроби нах. определитель кв.матрицы 2-го порядка. Опр-мый ф-ой (2) мн-н  имеет 1-ую степень и для него вып-ся инт. ус-я имеет 1-ую степень и для него вып-ся инт. ус-я   . Б. сч. тожд-ми обоз-я . Б. сч. тожд-ми обоз-я  и и  Тогда ф-ла (2) м.б. переписана в виде Тогда ф-ла (2) м.б. переписана в виде  . Выч-ое зн-е . Выч-ое зн-е  явл. 2-ым приближением к искомому зн-ию явл. 2-ым приближением к искомому зн-ию  . Это зн-е получается линейной инт-ей по ф-ле (2). На след. шаге сх.Эйткена из ост. табл. узлов . Это зн-е получается линейной инт-ей по ф-ле (2). На след. шаге сх.Эйткена из ост. табл. узлов  нах. ближ. к заданному зн-ию нах. ближ. к заданному зн-ию  и обозн. через (берется в качестве) и обозн. через (берется в качестве)  . Новое приближение к искомому значению вычисляется по формуле . Новое приближение к искомому значению вычисляется по формуле  (3) Перед этим предварительно должно быть вычислено (3) Перед этим предварительно должно быть вычислено  , которое вычисляется по формуле, аналогичной формуле (2), в которой все индексы должны быть увеличены на 1. Легко видеть, что при этом будут выполняться условия интерполяции , которое вычисляется по формуле, аналогичной формуле (2), в которой все индексы должны быть увеличены на 1. Легко видеть, что при этом будут выполняться условия интерполяции  , ,  .Если значения .Если значения  и и  совпадают в пределах требуемой точности, то вычисления прекращаются. В качестве окончательного результата берется значение совпадают в пределах требуемой точности, то вычисления прекращаются. В качестве окончательного результата берется значение  . В противном случае выбирается еще один узел интерполяции . В противном случае выбирается еще один узел интерполяции  и проводятся вычисления по формуле и проводятся вычисления по формуле  (4) при i=3 и k=1, 2, 3. Формула (4) является основной вычислительной формулой схемы Эйткена. (4) при i=3 и k=1, 2, 3. Формула (4) является основной вычислительной формулой схемы Эйткена.
Составление таблиц.
Для зад-ой ф-ии  требуется постр. на отрезке требуется постр. на отрезке  т-цу т-цу 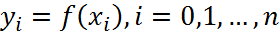 . При этом постоянный шаг таблицы h должен быть выбран так, чтобы таблица допускала инт-ию многочленом степени k с заданной точностью . При этом постоянный шаг таблицы h должен быть выбран так, чтобы таблица допускала инт-ию многочленом степени k с заданной точностью  . При решении поставленной задачи воспользуемся полученной оценкой остаточного члена инт. многочлена Лагранжа степени k по узлам . При решении поставленной задачи воспользуемся полученной оценкой остаточного члена инт. многочлена Лагранжа степени k по узлам 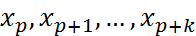 : : 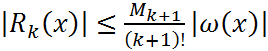 ,(1) где ,(1) где  , ,  . Т. о., шаг т-цы h следует выбрать так, чтобы уд-лось не-во . Т. о., шаг т-цы h следует выбрать так, чтобы уд-лось не-во  .(2)Проведем замену переменного по пр-лу .(2)Проведем замену переменного по пр-лу  . Т. не-во (2) принимает вид . Т. не-во (2) принимает вид 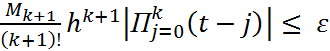 . Сл-но, искомое значение шага т-цы h должно уд. Не-ву . Сл-но, искомое значение шага т-цы h должно уд. Не-ву  (3)Здесь предп-ся, что зн-е ар-та x (3)Здесь предп-ся, что зн-е ар-та x  отрезку инт-ии отрезку инт-ии 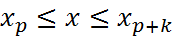 . Итак, задача нах-ия искомого значения шага таблицы h сводится к задаче нахождения max ф-ии . Итак, задача нах-ия искомого значения шага таблицы h сводится к задаче нахождения max ф-ии  на отрезке на отрезке  .В случае линейной инт-ии k=1имеем .В случае линейной инт-ии k=1имеем  . Решение уравнения . Решение уравнения  дает дает  . Т.о., т-ца допускает линейную инт-ию с заданной точностью, если ее шаг уд-ет неравенству . Т.о., т-ца допускает линейную инт-ию с заданной точностью, если ее шаг уд-ет неравенству  .(4) Для ф-ии .(4) Для ф-ии  имеем имеем  и при и при 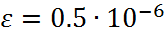 можно взять h=0.002. В случае квадратичной интерполяции k= 2имеем можно взять h=0.002. В случае квадратичной интерполяции k= 2имеем  . Решение Ур-ия . Решение Ур-ия 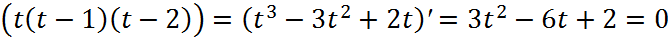 дает дает  .Получаем .Получаем
 . Т.о., т-ца допускает квадратичную инт-ю с заданной точностью, если ее шаг уд-ет не-ву . Т.о., т-ца допускает квадратичную инт-ю с заданной точностью, если ее шаг уд-ет не-ву  (5) Если при квадр-ой инт-ии выбирать узлы инт-ии так, чтобы таб-ый узел (5) Если при квадр-ой инт-ии выбирать узлы инт-ии так, чтобы таб-ый узел  был ближайшим к x,то.б вып. не-во был ближайшим к x,то.б вып. не-во  или или  и при выборе шага нужно находить только и при выборе шага нужно находить только  . Поскольку . Поскольку  , то ф-ия , то ф-ия 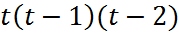 на отрезке на отрезке  монотонно убывает. Сл-но, монотонно убывает. Сл-но,  . В рез-те приходим к оценке шага т-цы . В рез-те приходим к оценке шага т-цы  .(6)Для ф-ии .(6)Для ф-ии  имеем имеем  и при и при 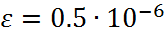 м.взять h= 0.02.Т-ца ф-ии y=sin x, доп-щая кв-ую инт-ию, требует для своего хр-ия в 10 раз < объема памяти, чем т-ца этой же ф-ии, доп-ая только лин-ую инт-ию. м.взять h= 0.02.Т-ца ф-ии y=sin x, доп-щая кв-ую инт-ию, требует для своего хр-ия в 10 раз < объема памяти, чем т-ца этой же ф-ии, доп-ая только лин-ую инт-ию.
Квадратурные формулы Гаусса
Опр. Говорят, что квадратурная формула
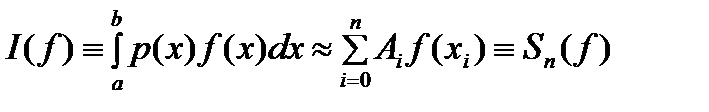 (1) (1)
имеет алгебраическую степень точности m, если она является точной для любого многочлена степени 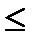 m и существует многочлен степени m и существует многочлен степени 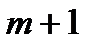 , для которого квадратурная формула не является точной. , для которого квадратурная формула не является точной.
Квадратурные формулы наивысшей алгебраической степени точности называют квадратурными формулами Гаусса (при этом n считается фиксированным). Квадратурное правило имеет алгебраическую степень точности не ниже n тогда и только тогда, когда оно является интерполяционным. Следовательно, коэффициенты квадратурных правил Гаусса определяются формулой
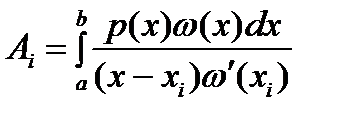 . (2) . (2)
Таким образом, остается найти оптимальный набор узлов, при котором интерполяционная квадратурная формула будет иметь наивысшую алгебраическую степень точности. Последняя, как будет доказано, равна  . .
Лемма 1. Если квадратурное правило (1) имеет алгебраическую степень точности  , то многочлен , то многочлен 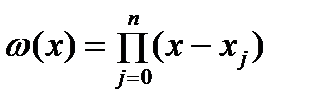 степени степени 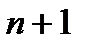 ортогонален с весом ортогонален с весом 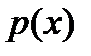 на отрезке на отрезке 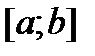 любому многочлену меньшей степени. любому многочлену меньшей степени.
Д-во. Так как квадратурное правило (1) является точным для любого многочлена степени  и и 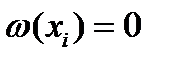 ,то при ,то при 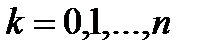 имеем имеем  , что док-ет лемму. , что док-ет лемму.
Из леммы 1 следует, что для построения квадратурного правила алгебраической степени точности  необходимо найти многочлен степени необходимо найти многочлен степени 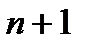 , который был бы ортогонален любому многочлену меньшей степени. , который был бы ортогонален любому многочлену меньшей степени.
Лемма 2. Если  почти всюду на почти всюду на 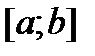 , то приведенный многочлен степени , то приведенный многочлен степени 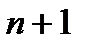 , ортогональный на , ортогональный на 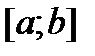 с весом с весом 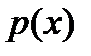 любому многочлену меньшей степени, существует и является единственным. При этом все его корни простые и находятся на отрезке любому многочлену меньшей степени, существует и является единственным. При этом все его корни простые и находятся на отрезке 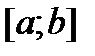 . .
Д-во. Для искомого приведенного многочлена 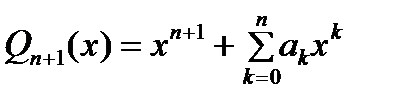 степени степени 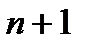 условия ортогональности любому многочлену меньшей степени дают систему линейных алгебраических уравнений условия ортогональности любому многочлену меньшей степени дают систему линейных алгебраических уравнений 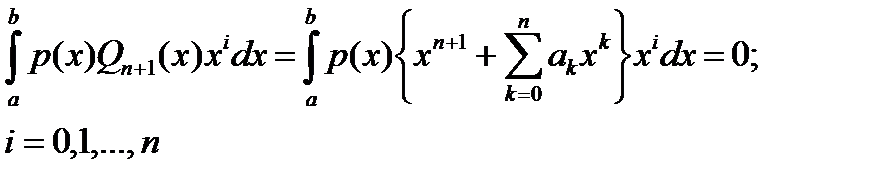 (3) (3)
относительно неизвестных коэффициентов 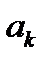 . Системе (3) соответствует однородная система . Системе (3) соответствует однородная система 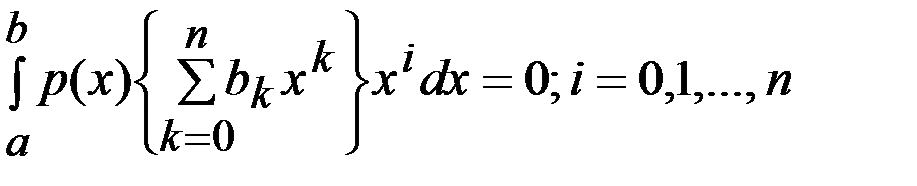 (4).Уравнения системы (4) умножим на соответствующие коэффициенты (4).Уравнения системы (4) умножим на соответствующие коэффициенты 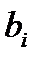 и сложим. Из полученного при этом выражения и сложим. Из полученного при этом выражения  и условия леммы и условия леммы  вытекает, что вытекает, что 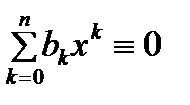 , т.е. , т.е. 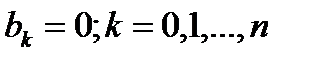 . Поскольку однородная система (4) имеет только тривиальное решение, то соответствующая неоднородная система (3) имеет единственное решение. . Поскольку однородная система (4) имеет только тривиальное решение, то соответствующая неоднородная система (3) имеет единственное решение.
Пусть 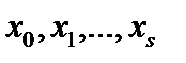 - корни нечетной кратности многочлена - корни нечетной кратности многочлена 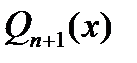 , лежащие на отрезке , лежащие на отрезке 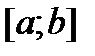 . Требуется доказать, что . Требуется доказать, что 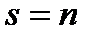 . Допустим противное: . Допустим противное:  . Тогда, в силу ортогональности, выполняется . Тогда, в силу ортогональности, выполняется 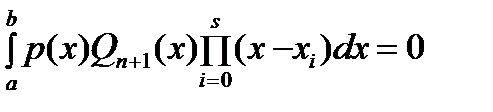 . С другой стороны, так как . С другой стороны, так как  и и 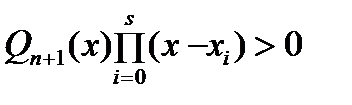 почти всюду на почти всюду на 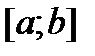 имеем имеем  . Полученное противоречие доказывает, что . Полученное противоречие доказывает, что 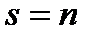 . Лемма доказана. . Лемма доказана.
Лемма 3. Если узлами интерполяционной квадратурной формулы (1) являются нули ортогонального многочлена  , то квадратурная формула точна для любого мн-на степени , то квадратурная формула точна для любого мн-на степени 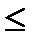  . .
Д-во. Пусть 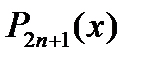 - произвольный многочлен степени - произвольный многочлен степени  . Представим его в виде . Представим его в виде  ,где ,где 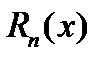 и и  -многочлены степени n. Имеем -многочлены степени n. Имеем
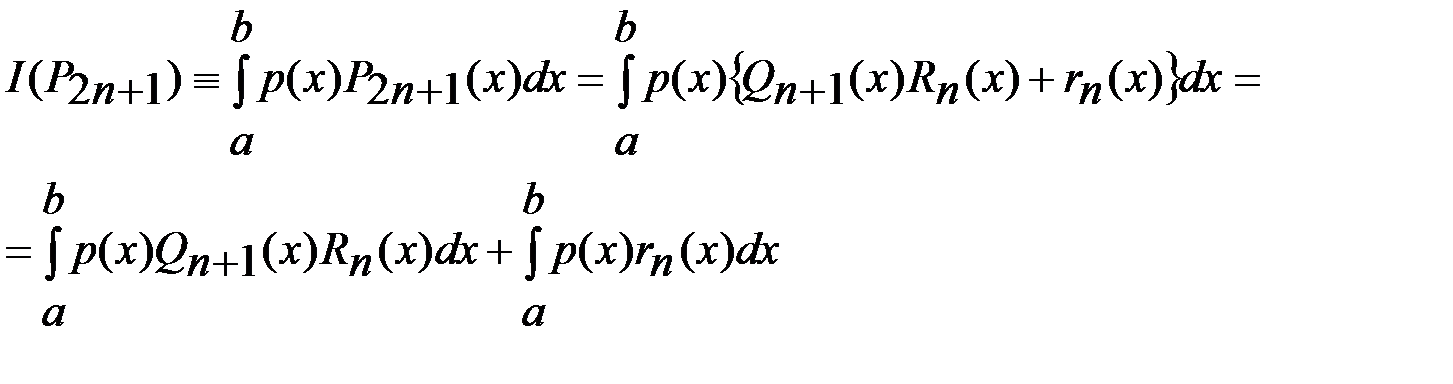 Здесь Здесь  в силу ортогональности в силу ортогональности  и, так как квадратурное правило интерполяционное, то и, так как квадратурное правило интерполяционное, то
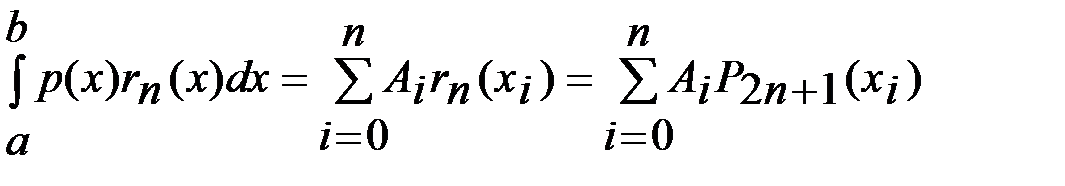 . Лемма доказана. . Лемма доказана.
Теорема. Если  почти всюду на почти всюду на  , то существует квадратурное правило (1) наивысшей алгебраической степени точности , то существует квадратурное правило (1) наивысшей алгебраической степени точности  . .
Д-во. Существование квадратурного правила (1) алгебр-кой степени точности  непосредственно следует из доказанных лемм. Остается доказать, что нельзя построить квадратурное правило (1), точное для любого многочлена степени непосредственно следует из доказанных лемм. Остается доказать, что нельзя построить квадратурное правило (1), точное для любого многочлена степени  . Для многочлена . Для многочлена 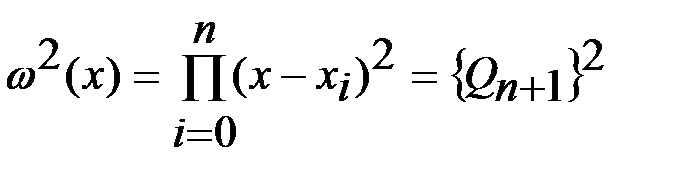 степени степени  имеем значение интеграла имеем значение интеграла  и значение квадратурной суммы и значение квадратурной суммы
 .Т-ма док-на. .Т-ма док-на.
19. Квадр-ные формулы Гаусса с постоянной весовой ф-ей. Рассмотрим интеграл 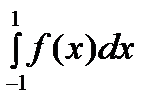 , (1) где , (1) где  - достаточно гладкая функция. Любой конечный отрезок интегрирования - достаточно гладкая функция. Любой конечный отрезок интегрирования 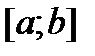 линейным преобразованием приводится к отрезку линейным преобразованием приводится к отрезку  . Поскольку в данном случае весовая функция . Поскольку в данном случае весовая функция 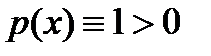 , то квадратурное правило наивысшей алгебраической степени точности , то квадратурное правило наивысшей алгебраической степени точности  (2)существует. Его узлами явл-ся корни мн-на (2)существует. Его узлами явл-ся корни мн-на  , ортогонального мн-нам меньшей степени с весом 1 на отрезке [-1;1]. , ортогонального мн-нам меньшей степени с весом 1 на отрезке [-1;1].
Обозначим 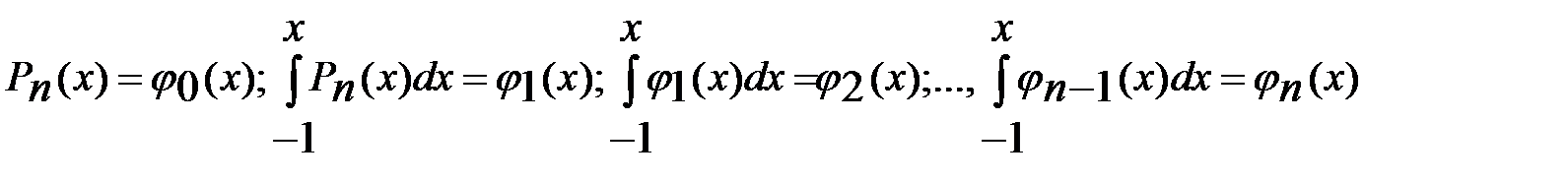 . Очевидно, . Очевидно, 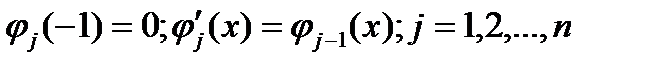 и и  . Возьмем произвольный многочлен . Возьмем произвольный многочлен 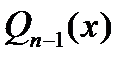 степени степени 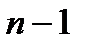 . Используя условия ортогональности и проводя интегрирование по частям, получим . Используя условия ортогональности и проводя интегрирование по частям, получим 
 . .
Продолжая процесс интегрирования по частям получим
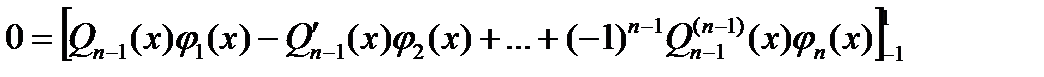 Отсюда для Отсюда для 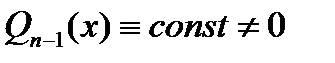 , следует, что , следует, что  . Используя произвольность многочлена . Используя произвольность многочлена 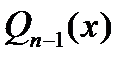 , последовательно получаем далее , последовательно получаем далее  . .
Таким образом, многочлен  степени степени 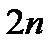 , производные которого определяются формулой , производные которого определяются формулой 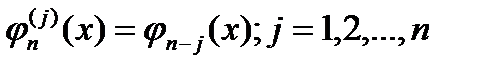 имеет корни имеет корни 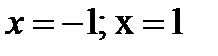 , каждый кратности n. Следовательно, этот многочлен представляется в виде , каждый кратности n. Следовательно, этот многочлен представляется в виде 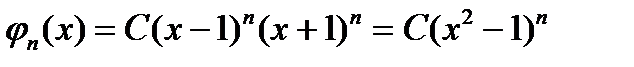 . Для искомого ортогонального многочлена в результате . Для искомого ортогонального многочлена в результате
получим выражение 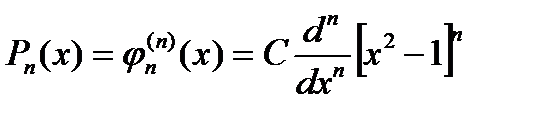 .(3) .(3)
Ортогональные многочлены, определяемые формулой (3) называют многочленами Лежандра. В случае выбора константы по правилу 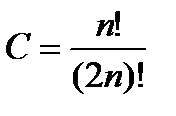 будут получаться приведенные многочлены. В практике вычислений для многочленов Лежандра используется формула Родрига будут получаться приведенные многочлены. В практике вычислений для многочленов Лежандра используется формула Родрига 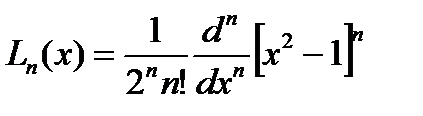 .(4) .(4)
При этом получается квадрат нормы  и рекуррентная формула и рекуррентная формула 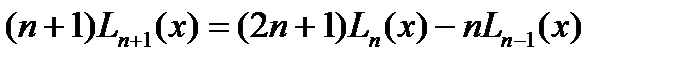 .(5) .(5)
По формуле(3) находим 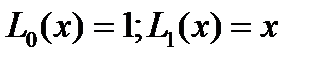 . По формуле (4) находим . По формуле (4) находим  . Отсюда определяем последовательно . Отсюда определяем последовательно
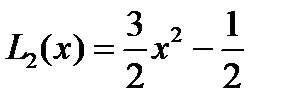 и и  . Построим несколько квадратурных формул Гаусса вида (2). . Построим несколько квадратурных формул Гаусса вида (2).
При 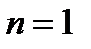 из уравнения из уравнения 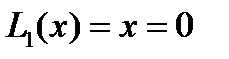 получаем один корень получаем один корень 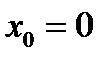 , , 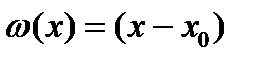 и один коэффициент и один коэффициент  . Приходим к квадратурной формуле . Приходим к квадратурной формуле 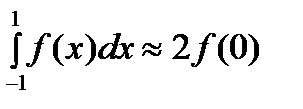 , имеющей наивысшую алгебраическую степень точности 1. , имеющей наивысшую алгебраическую степень точности 1.
При 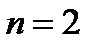 из уравнения из уравнения  получаем два корня получаем два корня 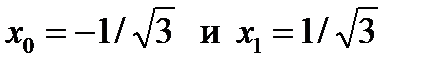 , ,  и два коэффициента и два коэффициента 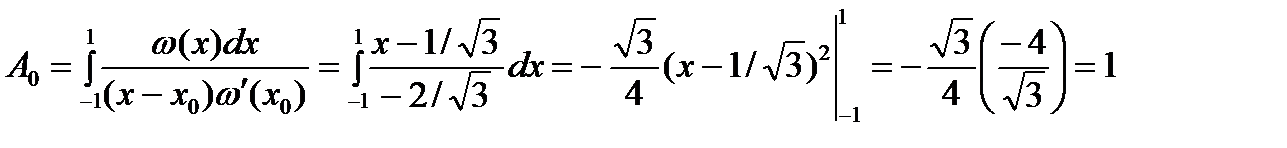 и и 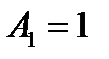 . Приходим к квадратурной формуле . Приходим к квадратурной формуле 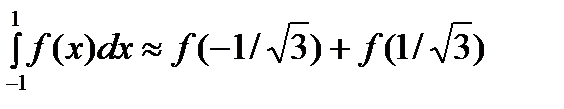 , имеющей наивысшую алгебр-скую степень точности 3. , имеющей наивысшую алгебр-скую степень точности 3.
Формула для вычисления коэффициентов квадратурной формулы (2) может быть преобразована к виду 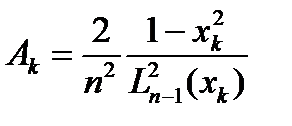 (6) (6)
При 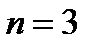 из уравнения из уравнения  получаем три корня получаем три корня 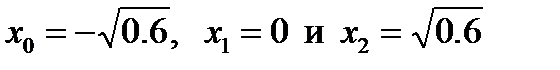 и три коэффициента и три коэффициента 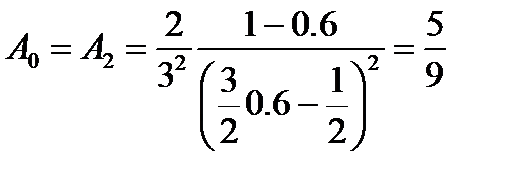 и и  . Приходим к квадратурной формуле . Приходим к квадратурной формуле 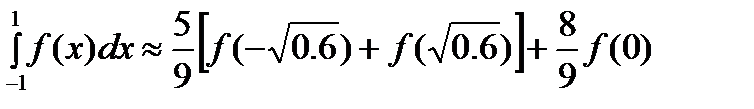 , имеющей наивысшую алгебраическую степень точности 5. , имеющей наивысшую алгебраическую степень точности 5.
Метод наименьших квадратов.
Пусть ф-ия f(x) задана табл. yi=f(xi); i=0,…n. Надо эту ф-ию приблизить ф-ей вида φ(x, a0,...,am). Знач-я неизвест-х парам-ов aj;j=0,...m надо выбрать т.ч. сумма кв-ов отклонений
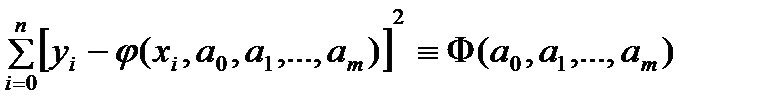 (1) ф-ии f от ф-ии φ по всем табл-ым узлам xi была мин-ой. Е. ф-ия φ явл. достаточно гладкой, то искомые зн. параметров м.б. найдены из условий Ферма (1) ф-ии f от ф-ии φ по всем табл-ым узлам xi была мин-ой. Е. ф-ия φ явл. достаточно гладкой, то искомые зн. параметров м.б. найдены из условий Ферма 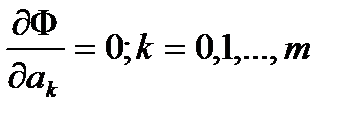 . (2) . (2)
Когда ф-ия φ линейно зависит от параметров:  , с-ма (2) будет линейной , с-ма (2) будет линейной  . После простых преобразований с-ма: . После простых преобразований с-ма:
 .(3) .(3)
Определитель  с-мы - определитель Грама с элементами Akj, равными скалярным произвед-ям с-мы - определитель Грама с элементами Akj, равными скалярным произвед-ям  . .
Теорема. Если последов-ть непрерывных ф-ций 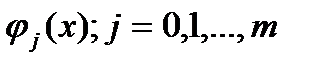 явл. сис-мой Чебышева на [a;b], то определитель с-мы (3) ≠ 0 при любых наборах попарно неравных узлов явл. сис-мой Чебышева на [a;b], то определитель с-мы (3) ≠ 0 при любых наборах попарно неравных узлов 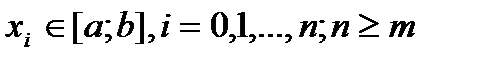 . .
Доказательство. Противное: последов-сть ф-ий явл. сис-мой Чебышева на отр-е, но 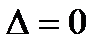 при некот-ом наборе попарно неравных узлов. Тогда столбцы определителя будут линейно зависимыми при некот-ом наборе попарно неравных узлов. Тогда столбцы определителя будут линейно зависимыми  . => . =>  . Умножая последние равенства на соответствующие ck и проводя суммирование по k, получим . Умножая последние равенства на соответствующие ck и проводя суммирование по k, получим
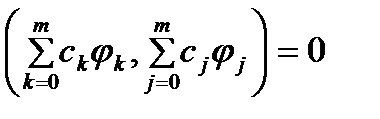 , откуда , откуда  . Т. о., нетривиальный обобщенный многочлен . Т. о., нетривиальный обобщенный многочлен 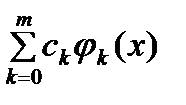 обращается в 0 на отрезке не менее чем в n+1 -й точке, что > m. Полученное противоречие доказывает теорему. обращается в 0 на отрезке не менее чем в n+1 -й точке, что > m. Полученное противоречие доказывает теорему.
При m=n единственным решение – интерполяц-ый обобщенный многочлен φ(x); при этом min сумма квадратов отклонений: Ф=0.
Сис-ма ф-ий 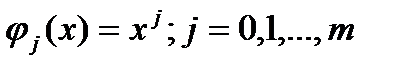 явл. сис-мой Чебышева на любом отр., поэтому наилучшее приближение табличной ф-ии yi=f(xi) алгебраическим многочленом явл. сис-мой Чебышева на любом отр., поэтому наилучшее приближение табличной ф-ии yi=f(xi) алгебраическим многочленом 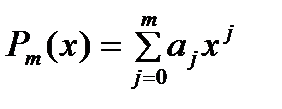 степени m<=n по методу наименьших квадратов сущ-ет, явл. единственным и коэффиценты многочлена м.б. найдены из линейной алгебраической системы степени m<=n по методу наименьших квадратов сущ-ет, явл. единственным и коэффиценты многочлена м.б. найдены из линейной алгебраической системы 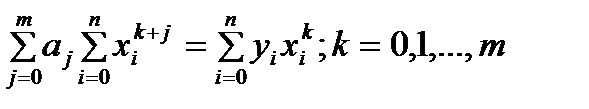 . При m=2 система: . При m=2 система:
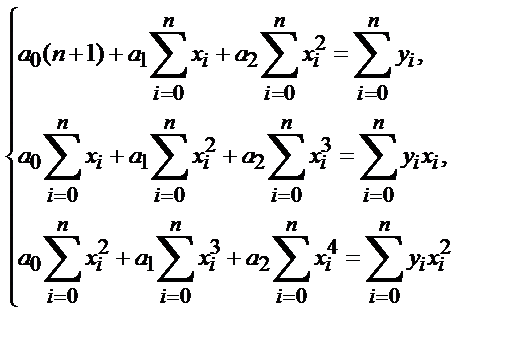
Многочлены наилучших равномерных приближений. Примеры.
Рассмотрим пр-во  - непрерывных на - непрерывных на  ф-ий. Пусть ф-ий. Пусть  . Будем рассматривать задачу аппроксимации ф-ии f многочленом . Будем рассматривать задачу аппроксимации ф-ии f многочленом  степени n. Если степень n не фиксир., то ф-ию f можно с любой точностью приблизить к соответствующим многочленам более точно справедлива следующая теорема. степени n. Если степень n не фиксир., то ф-ию f можно с любой точностью приблизить к соответствующим многочленам более точно справедлива следующая теорема.
Теорема Веерштрасса.  и и  что что 
Если число n –фиксировано, то ф-ию f уже нельзя приблизить с любой точностью к многочлену  однако для любой ф-ции однако для любой ф-ции   степени n, такой что степени n, такой что  , где , где  берётся по всевозможным многочленам степени n. Такой многочлен берётся по всевозможным многочленам степени n. Такой многочлен  наз. многочленом наилучшего равномерного приближения или Чебышевским приближением. Отметим, что не существует общего алгоритма построения мног. наз. многочленом наилучшего равномерного приближения или Чебышевским приближением. Отметим, что не существует общего алгоритма построения мног.  однако для построения этого многочлена можно использовать след. утв.: однако для построения этого многочлена можно использовать след. утв.:
Теорема Чебышева: Для того, чтобы многочлен  степени n был многочленом наилучшего равномерного приближения для ф-ии f необх. и достат., чтобы на степени n был многочленом наилучшего равномерного приближения для ф-ии f необх. и достат., чтобы на  существовали по крайней мере n+2 точки существовали по крайней мере n+2 точки  в которых в которых  где где  . .
Другими словами, теорема говорит о том, что в точках  поочерёдное отклонение ф-ции f от многочлена поочерёдное отклонение ф-ции f от многочлена  достигает наиб. значений. При этом точки достигает наиб. значений. При этом точки  наз. точками Чебышевского альтернанса. наз. точками Чебышевского альтернанса.
Пример1. Будем аппроксимировать ф-ию f многочлена нулевой степени  . Положим . Положим  . .
Положим  . Покажем, что в этом случае многочлен . Покажем, что в этом случае многочлен  есть многочлен наилучшего равномерного приближения. Имеем есть многочлен наилучшего равномерного приближения. Имеем

А точки в которых f(x)=m и f(x)=М образуют Чебышевский альтернанс.
Пример2. Пусть  и является выпуклой. Будем аппроксимировать ф-цию f многочленом и является выпуклой. Будем аппроксимировать ф-цию f многочленом  . .
Составим разность  Пусть С – точка экстремума ф-ции Пусть С – точка экстремума ф-ции  (очевидно, что такая точка существует, причём (очевидно, что такая точка существует, причём  ). Потребуем, чтобы точки а,с,в в указанном порядке образ. Чебышевский альтернанс. В этом случае будем иметь две системы уравнений: ). Потребуем, чтобы точки а,с,в в указанном порядке образ. Чебышевский альтернанс. В этом случае будем иметь две системы уравнений:

Относительно неизвестных Е, с,  .Заметим, что в данных системах через Е обозначено .Заметим, что в данных системах через Е обозначено  , а 4-ое уравнение каждой из систем есть условие того, что точка С – точка экстремума ф-ции , а 4-ое уравнение каждой из систем есть условие того, что точка С – точка экстремума ф-ции  . .
Интерполяционные сплайны.
Сплайн-функция - кусочно-полиномиальная ф-ия, определ-ая на [a;b], имеющ. на нем некот.число непрерывных произв-ых.В выч. практике исп-тся кубические сплайны(к.с.)- сплайн опр-ся с помощью многочленов 3-ей степени. Рассмотрим интерполяц-ый к.с.(и.к.с.) для ф-ии f(x), непрерывной на [a;b].
На[a;b]сетка: a=x0<...<xN=b (1),обознач. 
И.к.с для f(x) и данного набора узлов (1)-ф-ия S(x),удовлетв-ая условиям:
1) на каждом сегменте [xi-1;xi],i=1,..,N, S(x) -мночлен 3-ей степ-и
2) S(x), ее первая и вторая производные непрерывны на [a;b];
3) 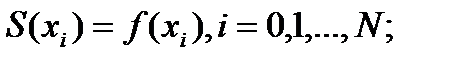 4) 4) 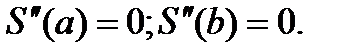
3) - усл-ие интерполирования. В 4) задаются граничные усл-ия.
Теорема. Для любой непрерывной ф-ии f(x) при любом наборе узлов (1) и.к.с S(x) сущ-ет и является единственным.
Д-во. существования - конструктивным методом. На каждом из отр.  б. искать ф-ию S(x)= Si(x) -многочлен 3-ей степени ( б. искать ф-ию S(x)= Si(x) -многочлен 3-ей степени ( ) )  (2) где (2) где  - коэфф-ты. ai найдем из усл-ий интерп-ния - коэфф-ты. ai найдем из усл-ий интерп-ния 
Доопределим,  Остальные коэфф-ты найдем из условий непрерывности 2) и граничных условий 4). Остальные коэфф-ты найдем из условий непрерывности 2) и граничных условий 4).
Из 2) для ф-ии S(x) во внутр-х узлах сетки Si-1(xi-1)=Si(xi-1), i=2..N и условия интерполир-ия  имеем имеем
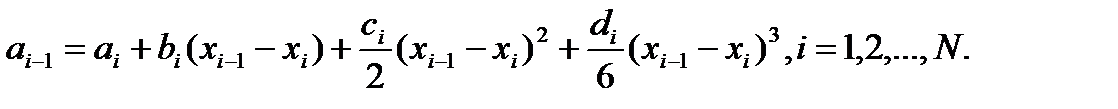 Пусть Пусть 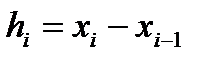 => =>  (3) (3)
Из усл-ия непрерывности 1-ой производной  во внутр-их узлах сетки во внутр-их узлах сетки  имеем имеем
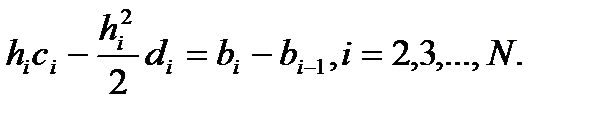 (4) (4)
Из усл-ия непрерывности 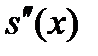 во внутр-их узлах сетки во внутр-их узлах сетки  и граничных условий и граничных условий 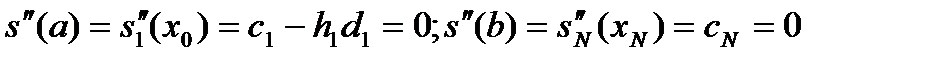 --> -->
 (5) где доопределено c0=0; (5) где доопределено c0=0;
Т.о., получена замкнутая сис-ма ур-ий (3), (4), (5) для опр-ия коэфф-ов к.с.. Покажем,ч. сис-ма имеет 1 решение. Перепишем (3) в виде  (6). Комбинируя 2 соседних ур-ия (6): (6). Комбинируя 2 соседних ур-ия (6):
 Подставляя найденное выражение для bi-bi-1 в пр. часть(4) получаем (7): Подставляя найденное выражение для bi-bi-1 в пр. часть(4) получаем (7):
 Из (5): Из (5):
 Подставляя это в (7), получаем сис-му ур-ний для ci : Подставляя это в (7), получаем сис-му ур-ний для ci : 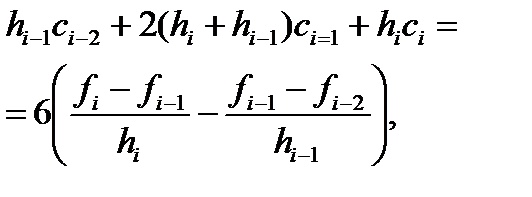  (8) В силу диагонального преобладания (8) имеет 1 решение. Т.к. матрица сис-мы трехдиагональная, решение - методом прогонки, кот. в данном случае устойчива. (8) В силу диагонального преобладания (8) имеет 1 решение. Т.к. матрица сис-мы трехдиагональная, решение - методом прогонки, кот. в данном случае устойчива. 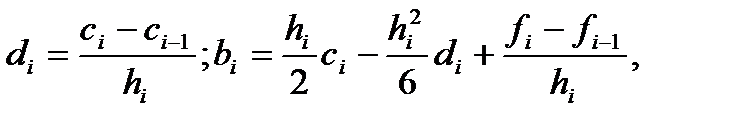  Ч.т.д. Ч.т.д.
Метод простой итерации.
Пусть на отрезке  задано уравнение в виде задано уравнение в виде  . (4) . (4)
|



 функций, определенных на отрезке
функций, определенных на отрезке  . Пусть в пространстве
. Пусть в пространстве  . Пусть также на отрезке
. Пусть также на отрезке  задана последовательность попарно неравных точек
задана последовательность попарно неравных точек  при
при  . Образуем линейную комбинацию
. Образуем линейную комбинацию  (1)
(1) .
. называют системой Чебышева на отрезке
называют системой Чебышева на отрезке  нужно приблизить обобщенным многочленом (1) так, чтобы значения функции и обобщенного многочлена совпадали в заданных точках:
нужно приблизить обобщенным многочленом (1) так, чтобы значения функции и обобщенного многочлена совпадали в заданных точках: . (2)
. (2) , удовлетворяющий условиям (2), называют интерполяционным обобщенным многочленом. При этом функцию
, удовлетворяющий условиям (2), называют интерполяционным обобщенным многочленом. При этом функцию  , для которой строится интерполяционный обобщенный многочлен, называют интерполируемой функцией, а точки
, для которой строится интерполяционный обобщенный многочлен, называют интерполируемой функцией, а точки  называют узлами интерполяции. Равенства (2) будем называть интерполяционными условиями.
называют узлами интерполяции. Равенства (2) будем называть интерполяционными условиями. при любых наборах попарно неравных узлов
при любых наборах попарно неравных узлов 
 существовал интерполяционный обобщенный многочлен по системе функций
существовал интерполяционный обобщенный многочлен по системе функций  , необходимо и достаточно, чтобы эта система функций была системой Чебышева на отрезке
, необходимо и достаточно, чтобы эта система функций была системой Чебышева на отрезке  . При этом интерполяционный обобщенный многочлен будет единственным.
. При этом интерполяционный обобщенный многочлен будет единственным.


 (1)
(1)
 . Система (1) имеет решение при любых правых частях тогда и только тогда, когда ее определитель
. Система (1) имеет решение при любых правых частях тогда и только тогда, когда ее определитель  отличен от нуля.
отличен от нуля. при любых наборах попарно неравных узлов на отрезке
при любых наборах попарно неравных узлов на отрезке  , а система функций
, а система функций  не является системой Чебышева на этом отрезке. Тогда существует нетривиальный обобщенный многочлен
не является системой Чебышева на этом отрезке. Тогда существует нетривиальный обобщенный многочлен 
 , который обращается в нуль на
, который обращается в нуль на  более чем в n точках. Возьмем n+ 1 из них в качестве узлов
более чем в n точках. Возьмем n+ 1 из них в качестве узлов 
 . Следовательно,
. Следовательно, 
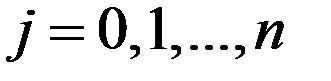 . Это означает, что столбцы определителя
. Это означает, что столбцы определителя  линейно зависимы и
линейно зависимы и  . Полученное противоречие доказывает необходимость.
. Полученное противоречие доказывает необходимость.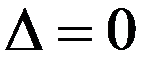 при некотором наборе попарно неравных узлов
при некотором наборе попарно неравных узлов 
 на этом отрезке. Следовательно, столбцы определителя линейно зависимы:
на этом отрезке. Следовательно, столбцы определителя линейно зависимы: 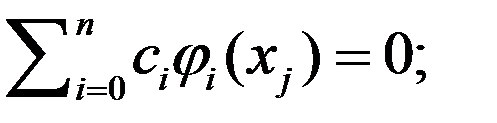
 . Последнее означает, что нетривиальный обобщенный многочлен
. Последнее означает, что нетривиальный обобщенный многочлен  обращается в нуль на
обращается в нуль на  система (1) имеет единственное решение, то интерполяционный обобщенный многочлен также будет при этом единственным. Теорема доказана.
система (1) имеет единственное решение, то интерполяционный обобщенный многочлен также будет при этом единственным. Теорема доказана.

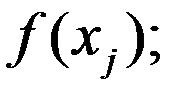
 (1) по ф-лам Крамера и выполним разложение
(1) по ф-лам Крамера и выполним разложение 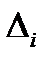 по столбцу i:
по столбцу i:  . Т.о., инт. об. мн-н м. представить в виде (2)
. Т.о., инт. об. мн-н м. представить в виде (2)



 .Интерполяционный многочлен Лагранжа. С-ма ф-ций
.Интерполяционный многочлен Лагранжа. С-ма ф-ций  , (1) в силу осн. теоремы алгебры, явл. с-мой Чебышева на любом отрезке. Для любой ф-ции
, (1) в силу осн. теоремы алгебры, явл. с-мой Чебышева на любом отрезке. Для любой ф-ции 
 ! инт. обоб. мн-н, к-ый м. б. записан в виде
! инт. обоб. мн-н, к-ый м. б. записан в виде  , (2) где обоб. мн-ны
, (2) где обоб. мн-ны  не зависят от ф-ии
не зависят от ф-ии  .Зафикс. j и рассм. ф-ию
.Зафикс. j и рассм. ф-ию  Для этой ф-ии имеем инт. обоб. мн-н
Для этой ф-ии имеем инт. обоб. мн-н  . Т.к. вып-ся инт. усл-я, то
. Т.к. вып-ся инт. усл-я, то  . Т.о., для обоб. мн-нов
. Т.о., для обоб. мн-нов  имеет место св-во
имеет место св-во  (3) Если построить обоб. мн-ны
(3) Если построить обоб. мн-ны 
 (1),очевидно, мн-ны
(1),очевидно, мн-ны  обл. св-м (3). Т.о., по с-ме ф-ий (3) инт-ый мн-н получается в виде
обл. св-м (3). Т.о., по с-ме ф-ий (3) инт-ый мн-н получается в виде  (4). (4) наз. инт.мн-м Лагранжа для ф-и
(4). (4) наз. инт.мн-м Лагранжа для ф-и  . Обозн.
. Обозн.  .имеем
.имеем 
 и
и  .С исп-ем мн-на
.С исп-ем мн-на  инт.мн-н Лагранжа примет вид
инт.мн-н Лагранжа примет вид  . (4’)
. (4’) задана на
задана на 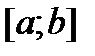 табл
табл  .(1) Треб. для заданного знач.
.(1) Треб. для заданного знач.  вычисл. приближ. знач. ф-и, исп-я инт. мн-н. Обозн. через
вычисл. приближ. знач. ф-и, исп-я инт. мн-н. Обозн. через 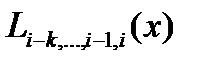 инт. мн-н, постр. для ф-и
инт. мн-н, постр. для ф-и  В сх. Эйткена сначала для заданного знач. арг.
В сх. Эйткена сначала для заданного знач. арг.  выб-ся ближ-й табл. узел среди всех табл-х узлов
выб-ся ближ-й табл. узел среди всех табл-х узлов  . Пусть это б. табл. узел
. Пусть это б. табл. узел  . Этот табл.узел берется в кач-ве узла инт-ии
. Этот табл.узел берется в кач-ве узла инт-ии  . Соотв.табл. зн-е ф-и
. Соотв.табл. зн-е ф-и  обозн.через
обозн.через 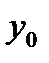 . Это табл.знач. м. сч. нач. приближением к иском. зн-ю ф-и в т.
. Это табл.знач. м. сч. нач. приближением к иском. зн-ю ф-и в т.  .Далее из ост. табл. узлов
.Далее из ост. табл. узлов  выбирается ближ. к
выбирается ближ. к  . Это б. или
. Это б. или  или
или  Найденный ближ. узел обозн.
Найденный ближ. узел обозн.  ,а соотв. табл. зн-е обозн.
,а соотв. табл. зн-е обозн.  Затем проводятся выч-я по ф-ле
Затем проводятся выч-я по ф-ле  .(2) Здесь в числителе дроби нах. определитель кв.матрицы 2-го порядка. Опр-мый ф-ой (2) мн-н
.(2) Здесь в числителе дроби нах. определитель кв.матрицы 2-го порядка. Опр-мый ф-ой (2) мн-н  имеет 1-ую степень и для него вып-ся инт. ус-я
имеет 1-ую степень и для него вып-ся инт. ус-я 
 . Б. сч. тожд-ми обоз-я
. Б. сч. тожд-ми обоз-я  и
и  Тогда ф-ла (2) м.б. переписана в виде
Тогда ф-ла (2) м.б. переписана в виде  . Выч-ое зн-е
. Выч-ое зн-е  явл. 2-ым приближением к искомому зн-ию
явл. 2-ым приближением к искомому зн-ию  . Это зн-е получается линейной инт-ей по ф-ле (2). На след. шаге сх.Эйткена из ост. табл. узлов
. Это зн-е получается линейной инт-ей по ф-ле (2). На след. шаге сх.Эйткена из ост. табл. узлов  нах. ближ. к заданному зн-ию
нах. ближ. к заданному зн-ию  и обозн. через (берется в качестве)
и обозн. через (берется в качестве)  . Новое приближение к искомому значению вычисляется по формуле
. Новое приближение к искомому значению вычисляется по формуле  (3) Перед этим предварительно должно быть вычислено
(3) Перед этим предварительно должно быть вычислено  , которое вычисляется по формуле, аналогичной формуле (2), в которой все индексы должны быть увеличены на 1. Легко видеть, что при этом будут выполняться условия интерполяции
, которое вычисляется по формуле, аналогичной формуле (2), в которой все индексы должны быть увеличены на 1. Легко видеть, что при этом будут выполняться условия интерполяции  ,
,  .Если значения
.Если значения  и
и  совпадают в пределах требуемой точности, то вычисления прекращаются. В качестве окончательного результата берется значение
совпадают в пределах требуемой точности, то вычисления прекращаются. В качестве окончательного результата берется значение  . В противном случае выбирается еще один узел интерполяции
. В противном случае выбирается еще один узел интерполяции  и проводятся вычисления по формуле
и проводятся вычисления по формуле  (4) при i=3 и k=1, 2, 3. Формула (4) является основной вычислительной формулой схемы Эйткена.
(4) при i=3 и k=1, 2, 3. Формула (4) является основной вычислительной формулой схемы Эйткена. требуется постр. на отрезке
требуется постр. на отрезке  т-цу
т-цу 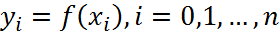 . При этом постоянный шаг таблицы h должен быть выбран так, чтобы таблица допускала инт-ию многочленом степени k с заданной точностью
. При этом постоянный шаг таблицы h должен быть выбран так, чтобы таблица допускала инт-ию многочленом степени k с заданной точностью  . При решении поставленной задачи воспользуемся полученной оценкой остаточного члена инт. многочлена Лагранжа степени k по узлам
. При решении поставленной задачи воспользуемся полученной оценкой остаточного члена инт. многочлена Лагранжа степени k по узлам 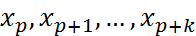 :
: 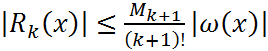 ,(1) где
,(1) где  ,
,  . Т. о., шаг т-цы h следует выбрать так, чтобы уд-лось не-во
. Т. о., шаг т-цы h следует выбрать так, чтобы уд-лось не-во  .(2)Проведем замену переменного по пр-лу
.(2)Проведем замену переменного по пр-лу  . Т. не-во (2) принимает вид
. Т. не-во (2) принимает вид 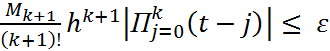 . Сл-но, искомое значение шага т-цы h должно уд. Не-ву
. Сл-но, искомое значение шага т-цы h должно уд. Не-ву  (3)Здесь предп-ся, что зн-е ар-та x
(3)Здесь предп-ся, что зн-е ар-та x  отрезку инт-ии
отрезку инт-ии 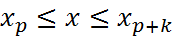 . Итак, задача нах-ия искомого значения шага таблицы h сводится к задаче нахождения max ф-ии
. Итак, задача нах-ия искомого значения шага таблицы h сводится к задаче нахождения max ф-ии  на отрезке
на отрезке  .В случае линейной инт-ии k=1имеем
.В случае линейной инт-ии k=1имеем  . Решение уравнения
. Решение уравнения  дает
дает  . Т.о., т-ца допускает линейную инт-ию с заданной точностью, если ее шаг уд-ет неравенству
. Т.о., т-ца допускает линейную инт-ию с заданной точностью, если ее шаг уд-ет неравенству  .(4) Для ф-ии
.(4) Для ф-ии  имеем
имеем  и при
и при 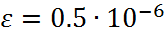 можно взять h=0.002. В случае квадратичной интерполяции k= 2имеем
можно взять h=0.002. В случае квадратичной интерполяции k= 2имеем  . Решение Ур-ия
. Решение Ур-ия 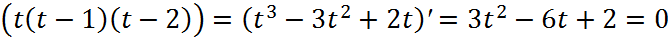 дает
дает  .Получаем
.Получаем . Т.о., т-ца допускает квадратичную инт-ю с заданной точностью, если ее шаг уд-ет не-ву
. Т.о., т-ца допускает квадратичную инт-ю с заданной точностью, если ее шаг уд-ет не-ву  (5) Если при квадр-ой инт-ии выбирать узлы инт-ии так, чтобы таб-ый узел
(5) Если при квадр-ой инт-ии выбирать узлы инт-ии так, чтобы таб-ый узел  был ближайшим к x,то.б вып. не-во
был ближайшим к x,то.б вып. не-во  или
или  и при выборе шага нужно находить только
и при выборе шага нужно находить только  . Поскольку
. Поскольку  , то ф-ия
, то ф-ия 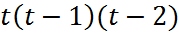 на отрезке
на отрезке  монотонно убывает. Сл-но,
монотонно убывает. Сл-но,  . В рез-те приходим к оценке шага т-цы
. В рез-те приходим к оценке шага т-цы  .(6)Для ф-ии
.(6)Для ф-ии  имеем
имеем  и при
и при 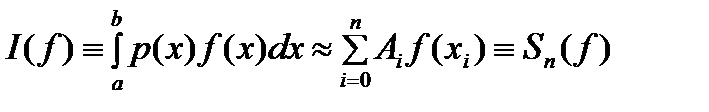 (1)
(1)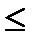 m и существует многочлен степени
m и существует многочлен степени 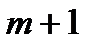 , для которого квадратурная формула не является точной.
, для которого квадратурная формула не является точной.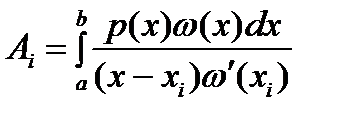 . (2)
. (2) .
.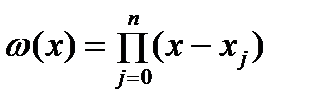 степени
степени 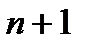 ортогонален с весом
ортогонален с весом 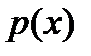 на отрезке
на отрезке 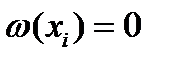 ,то при
,то при 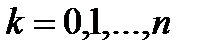 имеем
имеем  , что док-ет лемму.
, что док-ет лемму. почти всюду на
почти всюду на 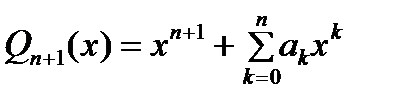 степени
степени 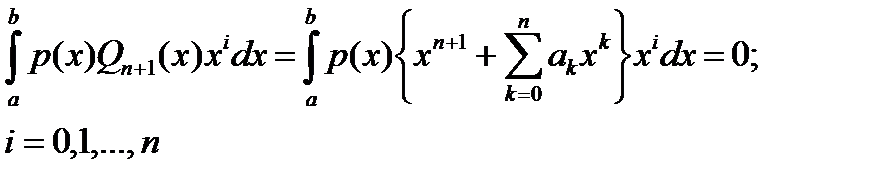 (3)
(3)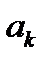 . Системе (3) соответствует однородная система
. Системе (3) соответствует однородная система 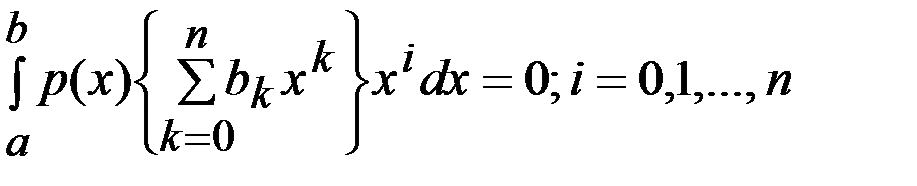 (4).Уравнения системы (4) умножим на соответствующие коэффициенты
(4).Уравнения системы (4) умножим на соответствующие коэффициенты 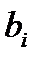 и сложим. Из полученного при этом выражения
и сложим. Из полученного при этом выражения  и условия леммы
и условия леммы 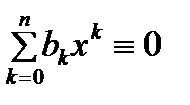 , т.е.
, т.е. 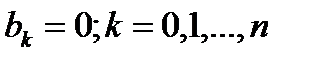 . Поскольку однородная система (4) имеет только тривиальное решение, то соответствующая неоднородная система (3) имеет единственное решение.
. Поскольку однородная система (4) имеет только тривиальное решение, то соответствующая неоднородная система (3) имеет единственное решение.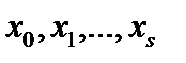 - корни нечетной кратности многочлена
- корни нечетной кратности многочлена 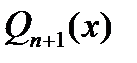 , лежащие на отрезке
, лежащие на отрезке 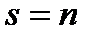 . Допустим противное:
. Допустим противное:  . Тогда, в силу ортогональности, выполняется
. Тогда, в силу ортогональности, выполняется 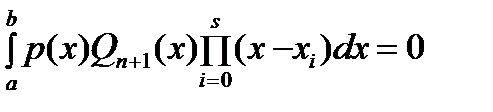 . С другой стороны, так как
. С другой стороны, так как 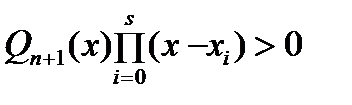 почти всюду на
почти всюду на  . Полученное противоречие доказывает, что
. Полученное противоречие доказывает, что  , то квадратурная формула точна для любого мн-на степени
, то квадратурная формула точна для любого мн-на степени 
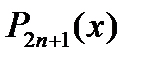 - произвольный многочлен степени
- произвольный многочлен степени  ,где
,где 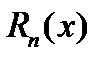 и
и  -многочлены степени n. Имеем
-многочлены степени n. Имеем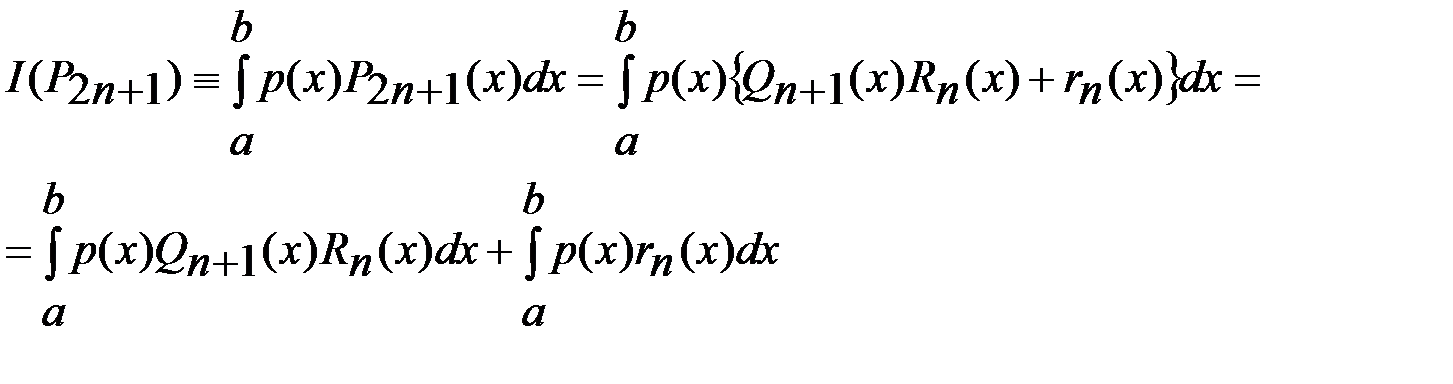 Здесь
Здесь  в силу ортогональности
в силу ортогональности 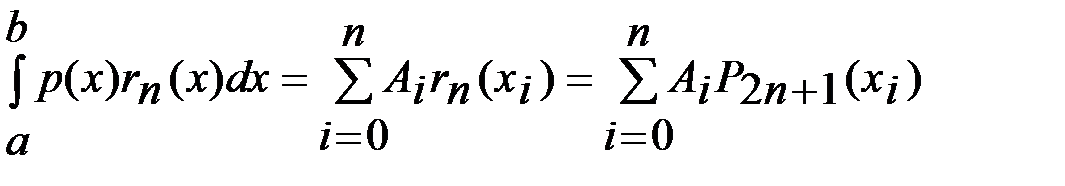 . Лемма доказана.
. Лемма доказана. . Для многочлена
. Для многочлена 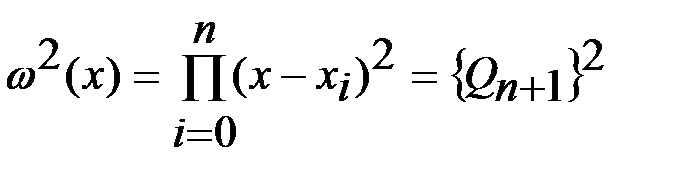 степени
степени  и значение квадратурной суммы
и значение квадратурной суммы .Т-ма док-на.
.Т-ма док-на. , (1) где
, (1) где  - достаточно гладкая функция. Любой конечный отрезок интегрирования
- достаточно гладкая функция. Любой конечный отрезок интегрирования  . Поскольку в данном случае весовая функция
. Поскольку в данном случае весовая функция 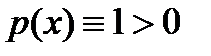 , то квадратурное правило наивысшей алгебраической степени точности
, то квадратурное правило наивысшей алгебраической степени точности  (2)существует. Его узлами явл-ся корни мн-на
(2)существует. Его узлами явл-ся корни мн-на  , ортогонального мн-нам меньшей степени с весом 1 на отрезке [-1;1].
, ортогонального мн-нам меньшей степени с весом 1 на отрезке [-1;1].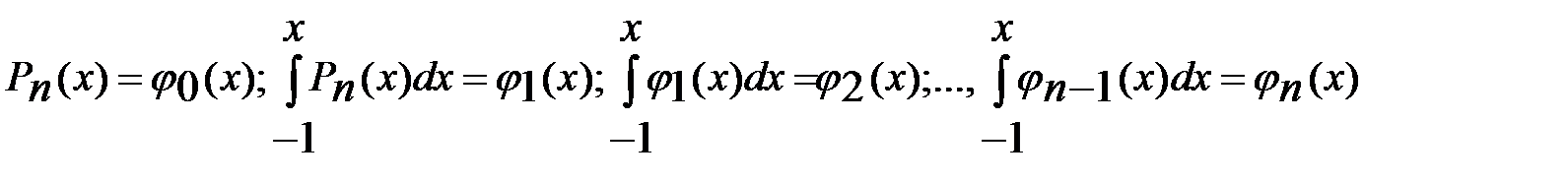 . Очевидно,
. Очевидно, 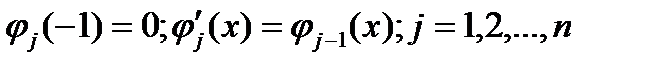 и
и  . Возьмем произвольный многочлен
. Возьмем произвольный многочлен 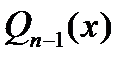 степени
степени 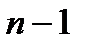 . Используя условия ортогональности и проводя интегрирование по частям, получим
. Используя условия ортогональности и проводя интегрирование по частям, получим 
 .
.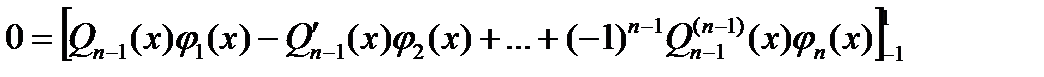 Отсюда для
Отсюда для 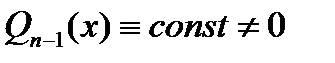 , следует, что
, следует, что  . Используя произвольность многочлена
. Используя произвольность многочлена  .
. степени
степени 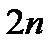 , производные которого определяются формулой
, производные которого определяются формулой 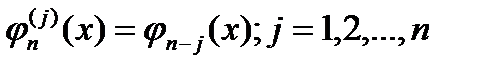 имеет корни
имеет корни 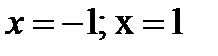 , каждый кратности n. Следовательно, этот многочлен представляется в виде
, каждый кратности n. Следовательно, этот многочлен представляется в виде 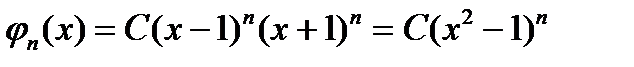 . Для искомого ортогонального многочлена в результате
. Для искомого ортогонального многочлена в результате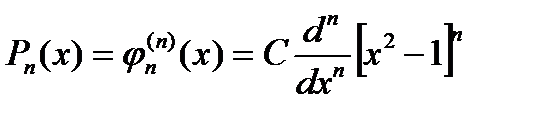 .(3)
.(3)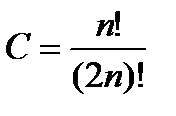 будут получаться приведенные многочлены. В практике вычислений для многочленов Лежандра используется формула Родрига
будут получаться приведенные многочлены. В практике вычислений для многочленов Лежандра используется формула Родрига 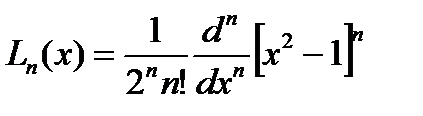 .(4)
.(4) и рекуррентная формула
и рекуррентная формула 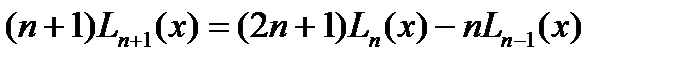 .(5)
.(5)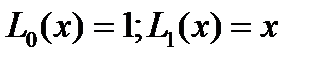 . По формуле (4) находим
. По формуле (4) находим  . Отсюда определяем последовательно
. Отсюда определяем последовательно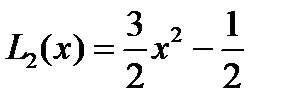 и
и  . Построим несколько квадратурных формул Гаусса вида (2).
. Построим несколько квадратурных формул Гаусса вида (2).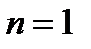 из уравнения
из уравнения 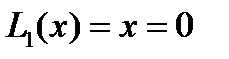 получаем один корень
получаем один корень 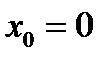 ,
, 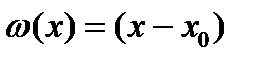 и один коэффициент
и один коэффициент  . Приходим к квадратурной формуле
. Приходим к квадратурной формуле 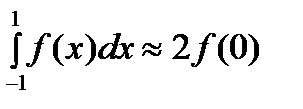 , имеющей наивысшую алгебраическую степень точности 1.
, имеющей наивысшую алгебраическую степень точности 1.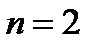 из уравнения
из уравнения  получаем два корня
получаем два корня 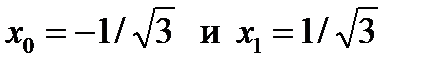 ,
,  и два коэффициента
и два коэффициента 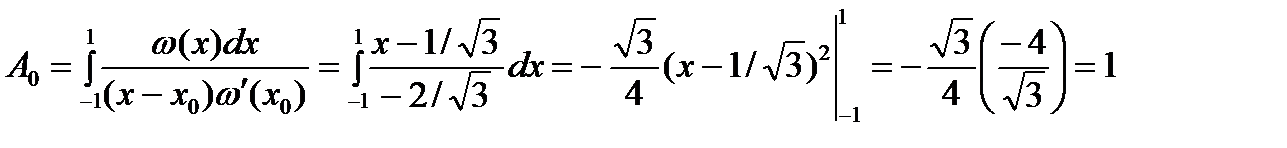 и
и 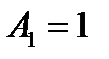 . Приходим к квадратурной формуле
. Приходим к квадратурной формуле 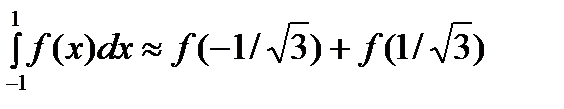 , имеющей наивысшую алгебр-скую степень точности 3.
, имеющей наивысшую алгебр-скую степень точности 3.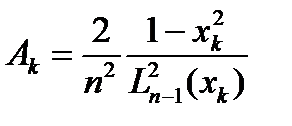 (6)
(6)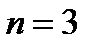 из уравнения
из уравнения  получаем три корня
получаем три корня 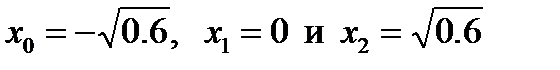 и три коэффициента
и три коэффициента 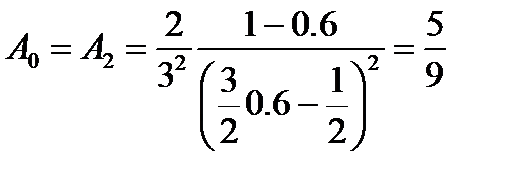 и
и  . Приходим к квадратурной формуле
. Приходим к квадратурной формуле 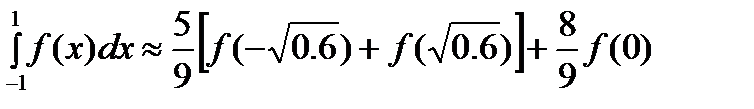 , имеющей наивысшую алгебраическую степень точности 5.
, имеющей наивысшую алгебраическую степень точности 5.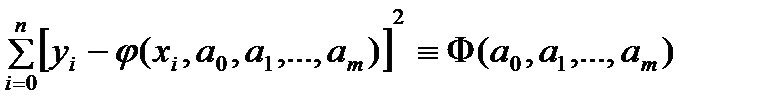 (1) ф-ии f от ф-ии φ по всем табл-ым узлам xi была мин-ой. Е. ф-ия φ явл. достаточно гладкой, то искомые зн. параметров м.б. найдены из условий Ферма
(1) ф-ии f от ф-ии φ по всем табл-ым узлам xi была мин-ой. Е. ф-ия φ явл. достаточно гладкой, то искомые зн. параметров м.б. найдены из условий Ферма 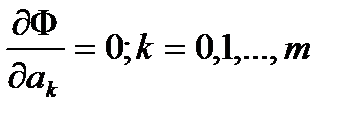 . (2)
. (2) , с-ма (2) будет линейной
, с-ма (2) будет линейной  . После простых преобразований с-ма:
. После простых преобразований с-ма: .(3)
.(3) .
.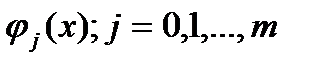 явл. сис-мой Чебышева на [a;b], то определитель с-мы (3) ≠ 0 при любых наборах попарно неравных узлов
явл. сис-мой Чебышева на [a;b], то определитель с-мы (3) ≠ 0 при любых наборах попарно неравных узлов 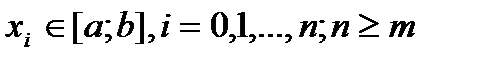 .
.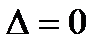 при некот-ом наборе попарно неравных узлов. Тогда столбцы определителя будут линейно зависимыми
при некот-ом наборе попарно неравных узлов. Тогда столбцы определителя будут линейно зависимыми  . =>
. =>  . Умножая последние равенства на соответствующие ck и проводя суммирование по k, получим
. Умножая последние равенства на соответствующие ck и проводя суммирование по k, получим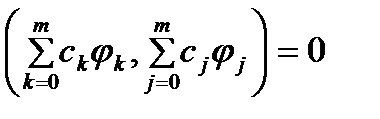 , откуда
, откуда  . Т. о., нетривиальный обобщенный многочлен
. Т. о., нетривиальный обобщенный многочлен 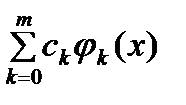 обращается в 0 на отрезке не менее чем в n+1 -й точке, что > m. Полученное противоречие доказывает теорему.
обращается в 0 на отрезке не менее чем в n+1 -й точке, что > m. Полученное противоречие доказывает теорему.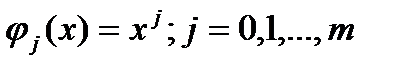 явл. сис-мой Чебышева на любом отр., поэтому наилучшее приближение табличной ф-ии yi=f(xi) алгебраическим многочленом
явл. сис-мой Чебышева на любом отр., поэтому наилучшее приближение табличной ф-ии yi=f(xi) алгебраическим многочленом 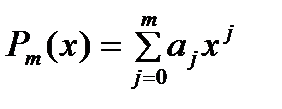 степени m<=n по методу наименьших квадратов сущ-ет, явл. единственным и коэффиценты многочлена м.б. найдены из линейной алгебраической системы
степени m<=n по методу наименьших квадратов сущ-ет, явл. единственным и коэффиценты многочлена м.б. найдены из линейной алгебраической системы 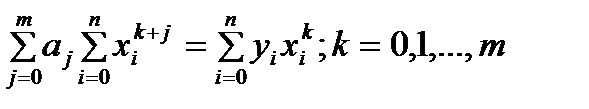 . При m=2 система:
. При m=2 система: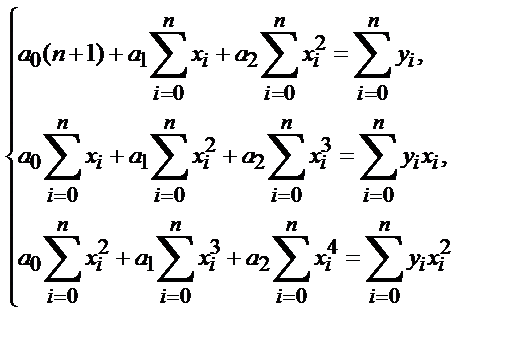
 - непрерывных на
- непрерывных на  ф-ий. Пусть
ф-ий. Пусть  . Будем рассматривать задачу аппроксимации ф-ии f многочленом
. Будем рассматривать задачу аппроксимации ф-ии f многочленом  степени n. Если степень n не фиксир., то ф-ию f можно с любой точностью приблизить к соответствующим многочленам более точно справедлива следующая теорема.
степени n. Если степень n не фиксир., то ф-ию f можно с любой точностью приблизить к соответствующим многочленам более точно справедлива следующая теорема. и
и  что
что 
 степени n, такой что
степени n, такой что  , где
, где  берётся по всевозможным многочленам степени n. Такой многочлен
берётся по всевозможным многочленам степени n. Такой многочлен  наз. многочленом наилучшего равномерного приближения или Чебышевским приближением. Отметим, что не существует общего алгоритма построения мног.
наз. многочленом наилучшего равномерного приближения или Чебышевским приближением. Отметим, что не существует общего алгоритма построения мног.  однако для построения этого многочлена можно использовать след. утв.:
однако для построения этого многочлена можно использовать след. утв.: степени n был многочленом наилучшего равномерного приближения для ф-ии f необх. и достат., чтобы на
степени n был многочленом наилучшего равномерного приближения для ф-ии f необх. и достат., чтобы на  существовали по крайней мере n+2 точки
существовали по крайней мере n+2 точки  в которых
в которых  где
где  .
. поочерёдное отклонение ф-ции f от многочлена
поочерёдное отклонение ф-ции f от многочлена  . Положим
. Положим  .
. . Покажем, что в этом случае многочлен
. Покажем, что в этом случае многочлен  есть многочлен наилучшего равномерного приближения. Имеем
есть многочлен наилучшего равномерного приближения. Имеем
 и является выпуклой. Будем аппроксимировать ф-цию f многочленом
и является выпуклой. Будем аппроксимировать ф-цию f многочленом  .
. Пусть С – точка экстремума ф-ции
Пусть С – точка экстремума ф-ции  (очевидно, что такая точка существует, причём
(очевидно, что такая точка существует, причём  ). Потребуем, чтобы точки а,с,в в указанном порядке образ. Чебышевский альтернанс. В этом случае будем иметь две системы уравнений:
). Потребуем, чтобы точки а,с,в в указанном порядке образ. Чебышевский альтернанс. В этом случае будем иметь две системы уравнений:
 .Заметим, что в данных системах через Е обозначено
.Заметим, что в данных системах через Е обозначено  , а 4-ое уравнение каждой из систем есть условие того, что точка С – точка экстремума ф-ции
, а 4-ое уравнение каждой из систем есть условие того, что точка С – точка экстремума ф-ции 
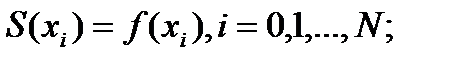 4)
4) 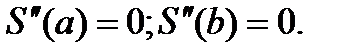
 б. искать ф-ию S(x)= Si(x) -многочлен 3-ей степени (
б. искать ф-ию S(x)= Si(x) -многочлен 3-ей степени ( )
)  (2) где
(2) где  - коэфф-ты. ai найдем из усл-ий интерп-ния
- коэфф-ты. ai найдем из усл-ий интерп-ния 
 Остальные коэфф-ты найдем из условий непрерывности 2) и граничных условий 4).
Остальные коэфф-ты найдем из условий непрерывности 2) и граничных условий 4). имеем
имеем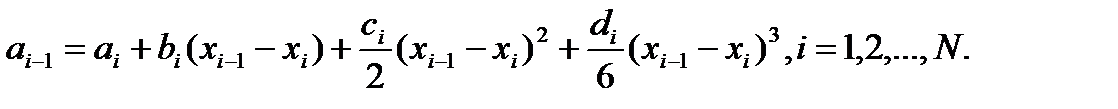 Пусть
Пусть 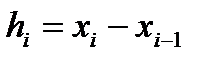 =>
=>  (3)
(3) во внутр-их узлах сетки
во внутр-их узлах сетки  имеем
имеем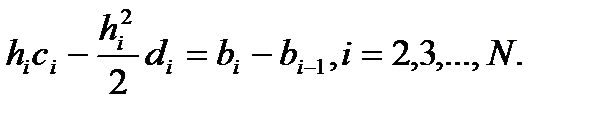 (4)
(4) во внутр-их узлах сетки
во внутр-их узлах сетки  и граничных условий
и граничных условий 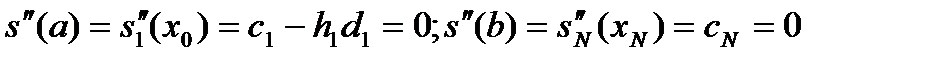 -->
--> (5) где доопределено c0=0;
(5) где доопределено c0=0; (6). Комбинируя 2 соседних ур-ия (6):
(6). Комбинируя 2 соседних ур-ия (6): Подставляя найденное выражение для bi-bi-1 в пр. часть(4) получаем (7):
Подставляя найденное выражение для bi-bi-1 в пр. часть(4) получаем (7): Из (5):
Из (5): Подставляя это в (7), получаем сис-му ур-ний для ci :
Подставляя это в (7), получаем сис-му ур-ний для ci : 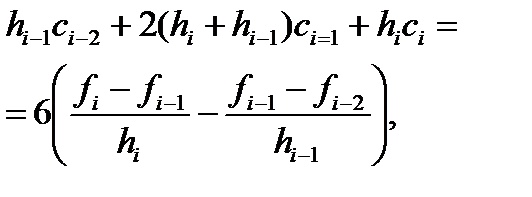
 (8) В силу диагонального преобладания (8) имеет 1 решение. Т.к. матрица сис-мы трехдиагональная, решение - методом прогонки, кот. в данном случае устойчива.
(8) В силу диагонального преобладания (8) имеет 1 решение. Т.к. матрица сис-мы трехдиагональная, решение - методом прогонки, кот. в данном случае устойчива. 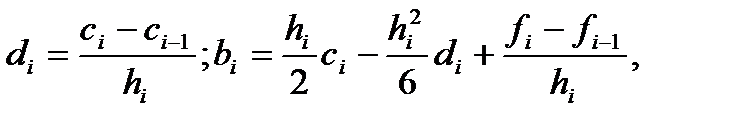
 Ч.т.д.
Ч.т.д. задано уравнение в виде
задано уравнение в виде  . (4)
. (4)


