
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Разделенные разности и интерполяционная формула Ньютона с разделенными разностями.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Ф-ия
Здесь разд.раз-ти 0-го порядка совпадают со значениями функции Лемма. Для разд.раз-й справедливо равенство
Док-во. По методу мат. индукции. При
Далее предположим, что (2) верна для всех разд. разн-й порядка
Интерполяц. многочлен Ньютона с разд. разн-ми. Через
Конечные разности и интерполяционные формулы Ньютона с конечными разностями. Пусть ф-ия
Пусть ф-ла (2) справедлива для раз-ей порядка k-1. Т.имеем
Заменим в формуле (5) разд. р-ти конечными в соответствии с формулой (6). Получим В формуле (7) сделаем замену переменной по пр-лу Ф-лу (7′) наз-ют инт. формулой Ньютона для инт-ия в конце табл. или для инт-ия назад. Здесь имеется в виду, что при
Составление таблиц. Для зад-ой ф-ии
|
||||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 604; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.117.89 (0.006 с.) |

 на
на  задана табл.
задана табл.  ,
, 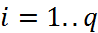 . Разд.раз-ти
. Разд.раз-ти  порядка k опр. рекуррентно ч-з разд.раз-ти порядка
порядка k опр. рекуррентно ч-з разд.раз-ти порядка 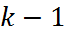 р-вом
р-вом (1)
(1) в узлах.
в узлах. (2)
(2) получаем
получаем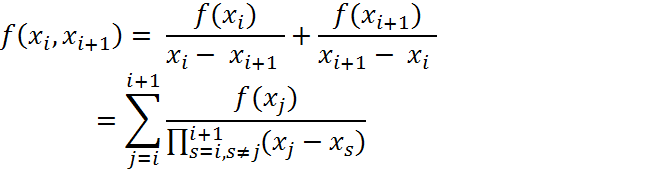
 порядка
порядка Лемма док-на. Из нее =>, что разд. разн-ти явл. симметричными функциями своих арг-тов.
Лемма док-на. Из нее =>, что разд. разн-ти явл. симметричными функциями своих арг-тов. будем обозначать интерпол. многочлен Лагранжа для ф-и
будем обозначать интерпол. многочлен Лагранжа для ф-и  , построен. по узлам
, построен. по узлам  ,
,  Рассмотрим очевидное тож-во
Рассмотрим очевидное тож-во  (1). Разность
(1). Разность  есть мн-н степени
есть мн-н степени  с корнями
с корнями  ,т.к. в силу инт. условий при
,т.к. в силу инт. условий при  имеем
имеем  . Поэтому
. Поэтому  (2) Положим в (2)
(2) Положим в (2)  и найдем константу
и найдем константу  :
: 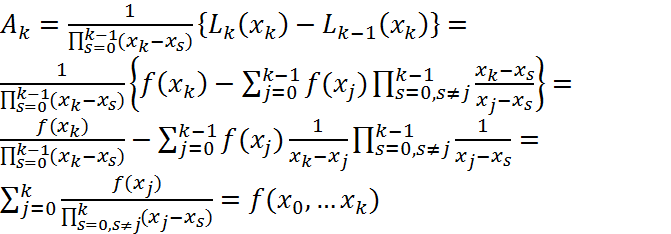 . Итак, получили
. Итак, получили 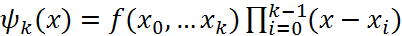 . Теперь (1) можно записать в виде
. Теперь (1) можно записать в виде 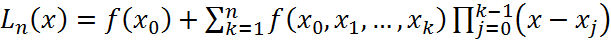 (3) Ф-лу (3) наз. инт. ф-лой Ньютона с разд. разностями.
(3) Ф-лу (3) наз. инт. ф-лой Ньютона с разд. разностями. на отрезке
на отрезке  задана табл.
задана табл.  с равноотстоящими узлами
с равноотстоящими узлами  . Конечные раз-ти
. Конечные раз-ти  порядка k опр. рекуррентно через конечные раз-ти порядка k-1рав-ом
порядка k опр. рекуррентно через конечные раз-ти порядка k-1рав-ом  (1). Здесь конечные раз-ти нулевого порядка берутся равными значениям
(1). Здесь конечные раз-ти нулевого порядка берутся равными значениям  функции в узлах. Лемма. Разд. раз-ти в случае равноотстоящих узлов выр-ся ч-з конечные раз-ти по формуле
функции в узлах. Лемма. Разд. раз-ти в случае равноотстоящих узлов выр-ся ч-з конечные раз-ти по формуле 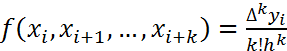 (2). Доказательство. Для случая k=1проверяем формулу непосредственно
(2). Доказательство. Для случая k=1проверяем формулу непосредственно .
. .Лемма доказана. В случае выбора в качестве узлов инт. табл. узлов
.Лемма доказана. В случае выбора в качестве узлов инт. табл. узлов  ф-ла Ньютона с разд-ми разн-ми принимает вид
ф-ла Ньютона с разд-ми разн-ми принимает вид  (3)Заменим в ней разд. раз-ти конечными в соответствии с (2). Получим
(3)Заменим в ней разд. раз-ти конечными в соответствии с (2). Получим (4). В формуле (4) сделаем замену переменной по правилу
(4). В формуле (4) сделаем замену переменной по правилу  (4′). Формулу (4′) наз инт. ф-й Ньютона для инт-ия в начале таблицы или для инт. вперед. Здесь имеется в виду, что при p = 0 первый узел инт-ии совп. с начальным узлом т-цы и ост. инт. узлы расп-ся от него вниз (вперед) по таблице. В качестве узлов инт-ии возьмем теперь табличные узлы
(4′). Формулу (4′) наз инт. ф-й Ньютона для инт-ия в начале таблицы или для инт. вперед. Здесь имеется в виду, что при p = 0 первый узел инт-ии совп. с начальным узлом т-цы и ост. инт. узлы расп-ся от него вниз (вперед) по таблице. В качестве узлов инт-ии возьмем теперь табличные узлы 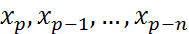 . Т. инт. формула Ньютона с разд. раз-ми при-ет вид
. Т. инт. формула Ньютона с разд. раз-ми при-ет вид  . (5)Так как разд. разности явл-ся сим-ми f-ми своих аргументов, то по формуле (2) имеем
. (5)Так как разд. разности явл-ся сим-ми f-ми своих аргументов, то по формуле (2) имеем  . (6)
. (6) .(7)
.(7) :
:  (7′)
(7′) первый узел инт-ии совпадает с последним узлом таблицы и остальные инт-ые узлы расп-ся от него вверх (назад) по таблице. Зам. В кач. нач. узла инт-ии обычно выб-ся табл. узел
первый узел инт-ии совпадает с последним узлом таблицы и остальные инт-ые узлы расп-ся от него вверх (назад) по таблице. Зам. В кач. нач. узла инт-ии обычно выб-ся табл. узел  , ближайший к зад. значению аргумента x. Далее выч.
, ближайший к зад. значению аргумента x. Далее выч.  . Если
. Если  , в качестве инт-ых берутся табл. узлы вниз от
, в качестве инт-ых берутся табл. узлы вниз от  и выч. пров-ся по инт. Ф-е Ньютона (4′) для инт. в начале таблицы. В случае когда
и выч. пров-ся по инт. Ф-е Ньютона (4′) для инт. в начале таблицы. В случае когда  , в кач-е инт. берутся табл. узлы вверх от
, в кач-е инт. берутся табл. узлы вверх от  требуется постр. на отрезке
требуется постр. на отрезке 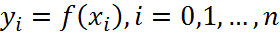 . При этом постоянный шаг таблицы h должен быть выбран так, чтобы таблица допускала инт-ию многочленом степени k с заданной точностью
. При этом постоянный шаг таблицы h должен быть выбран так, чтобы таблица допускала инт-ию многочленом степени k с заданной точностью  . При решении поставленной задачи воспользуемся полученной оценкой остаточного члена инт. многочлена Лагранжа степени k по узлам
. При решении поставленной задачи воспользуемся полученной оценкой остаточного члена инт. многочлена Лагранжа степени k по узлам 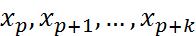 :
: 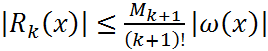 ,(1) где
,(1) где  ,
,  . Т. о., шаг т-цы h следует выбрать так, чтобы уд-лось не-во
. Т. о., шаг т-цы h следует выбрать так, чтобы уд-лось не-во  .(2)Проведем замену переменного по пр-лу
.(2)Проведем замену переменного по пр-лу  . Т. не-во (2) принимает вид
. Т. не-во (2) принимает вид 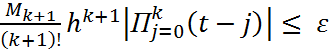 . Сл-но, искомое значение шага т-цы h должно уд. Не-ву
. Сл-но, искомое значение шага т-цы h должно уд. Не-ву  (3)Здесь предп-ся, что зн-е ар-та x
(3)Здесь предп-ся, что зн-е ар-та x  отрезку инт-ии
отрезку инт-ии 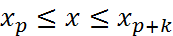 . Итак, задача нах-ия искомого значения шага таблицы h сводится к задаче нахождения max ф-ии
. Итак, задача нах-ия искомого значения шага таблицы h сводится к задаче нахождения max ф-ии  на отрезке
на отрезке  .В случае линейной инт-ии k=1имеем
.В случае линейной инт-ии k=1имеем  . Решение уравнения
. Решение уравнения  дает
дает  . Т.о., т-ца допускает линейную инт-ию с заданной точностью, если ее шаг уд-ет неравенству
. Т.о., т-ца допускает линейную инт-ию с заданной точностью, если ее шаг уд-ет неравенству  .(4) Для ф-ии
.(4) Для ф-ии  имеем
имеем  и при
и при 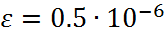 можно взять h=0.002. В случае квадратичной интерполяции k= 2имеем
можно взять h=0.002. В случае квадратичной интерполяции k= 2имеем  . Решение Ур-ия
. Решение Ур-ия 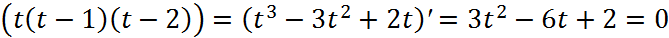 дает
дает  .Получаем
.Получаем . Т.о., т-ца допускает квадратичную инт-ю с заданной точностью, если ее шаг уд-ет не-ву
. Т.о., т-ца допускает квадратичную инт-ю с заданной точностью, если ее шаг уд-ет не-ву  (5) Если при квадр-ой инт-ии выбирать узлы инт-ии так, чтобы таб-ый узел
(5) Если при квадр-ой инт-ии выбирать узлы инт-ии так, чтобы таб-ый узел  был ближайшим к x,то.б вып. не-во
был ближайшим к x,то.б вып. не-во  или
или  и при выборе шага нужно находить только
и при выборе шага нужно находить только  . Поскольку
. Поскольку  , то ф-ия
, то ф-ия 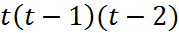 на отрезке
на отрезке  монотонно убывает. Сл-но,
монотонно убывает. Сл-но,  . В рез-те приходим к оценке шага т-цы
. В рез-те приходим к оценке шага т-цы  .(6)Для ф-ии
.(6)Для ф-ии  имеем
имеем  и при
и при 


