
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Разность между значениями функции в соседних узлах интерполяции называетсяСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте центральной разностью первого порядка; +конечной разностью первого порядка; разделенной разностью первого порядка. 60. Центральные табличные разности используются в интерполяционной формуле Ньютона для равноотстоящих узлов интерполяции; +Гаусса для равноотстоящих узлов интерполяции; Эйткина для равноотстоящих узлов интерполяции; Максимальная сумма модулей элементов матрицы по столбцам есть +норма 2; норма 3; норма 1.
62. Норма 3 матрицы 38; 26; +26,4244. 63. Итерационный процесс построения приближений по формуле +методом Зейделя; методом Ньютона; методом итерации. 64. Идея метода хорд состоит в том, что на достаточно малом промежутке +
Если уравнение полное, то +количество его положительных корней равно числу перемен знака количество его положительных корней равно числу постоянств количество его положительных корней равно числу постоянств величин отрицательных коэффициентов Конечные табличные разности используются в интерполяционной формуле +Ньютона; Гаусса; Эйткина; Лагранжа. Разделенные табличные разности используются в интерполяционной формуле Ньютона для равноотстоящих узлов интерполяции; Гаусса для равноотстоящих узлов интерполяции; +Ньютона для неравноотстоящих узлов интерполяции; Эйткина для равноотстоящих узлов интерполяции; Лагранжа для неравноотстоящих узлов интерполяции. 68. Корень квадратный из суммы квадратов модулей всех элементов матрицы есть норма 2; +норма 3; норма 1.
69. Норма 2 матрицы 38; +26; 26,4244. 70. Процесс интеграции для системы больше единицы; +меньше единицы; равно единице. Если для получения значения функции по данному значению аргумента нужно выполнить арифметические операции и возведение в степень с рациональным показателем, то функция называется +алгебраической; трансцендентной; рациональной. 72. Идея метода касательных состоит в том, что на достаточно малом промежутке
+ 73. Число действительных корней уравнения один положительный корень, два отрицательных корня; +два положительных корня, один отрицательный корень; три положительных корня.
Центральные табличные разности используются в интерполяционной формуле Ньютона; +Гаусса; Эйткина; Лагранжа. 75. Норма 1 матрицы 30; +39; 28,6356. 76. Норма 1 матрицы +38; 26; 26,4244. 77. Если для получения значения функции по данному значению алгебраической; трансцендентной; +рациональной. 78. Идея метода итерации состоит в том, что уравнение
+
79. Отделение корней уравнения
+
80. Процесс вычисления значений функции в точках +интерполированием; дифференцированием; интегрированием.
|
||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 1244; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.007 с.) |

 равна
равна называется
называется дуга кривой
дуга кривой  заменяется стягивающей её хордой. В качестве приближенного значения корня принимается точка пересечения хорды с осью
заменяется стягивающей её хордой. В качестве приближенного значения корня принимается точка пересечения хорды с осью  . Координаты этой точки определяются формулой
. Координаты этой точки определяются формулой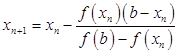 ;
; ;
; .
. ;
; равна
равна сходится к единственному решению независимо от выбора начального вектора, если сумма модулей элементов строк или сумма модулей столбцов
сходится к единственному решению независимо от выбора начального вектора, если сумма модулей элементов строк или сумма модулей столбцов дуга кривой
дуга кривой  заменяется касательной к этой кривой. В качестве приближенного значения корня принимается точка пересечения касательной с осью
заменяется касательной к этой кривой. В качестве приближенного значения корня принимается точка пересечения касательной с осью  ;
; ;
;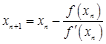 .
. по правилу Штурма равно
по правилу Штурма равно равна
равна равна
равна
 . В качестве
. В качестве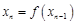 ;
; ;
; ;
; .
. , отличных
, отличных


