
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Полиномиальная интерполяция с кратными узламиСодержание книги
Поиск на нашем сайте
Пусть дана дискретная функция f(х) в узлах х0, х1...хm (хk<хk+1,
Требуется построить многочлен Qn(х) n-ой степени, совпадающий в узлах со всеми этими значениями, т.е. получим систему:
Интерполяционный многочлен Qn(х) определяется единственным образом. Действительно, предположим, что существует многочлен
Т.е. точки х0...хm – нули многочлена Рn(х) кратности S0...Sm соответственно. Получено: многочлен Рn(х)≠0 степени n имеет n+1 нулей (из кратности). Отсюда, Рn(х)≡0. Противоречие доказывает требуемое. Таким образом, линейная алгебраическая система невырождена, и её решение находится единственным образом.
Погрешность интерполяции. Обозначим f(х):=Qn(х)+Rn(х). Представим погрешность Rn в виде:
Отсюда, где S=0...Sk-1; φ(хk)=0; k=0, 1...m (т.е. хk – нули кратности S0...Sm соответственно). Выберем k из условия φ(х')=0, где х' – точка, в которой оценивается погрешность Из уравнения φ(х')=0 получим:
Будем предполагать, что Следовательно, по Т. Ролля φ'(х) обращается в ноль в по крайней мере (n+1) точке. ........................................................................... Тогда, по Т. Ролля φ(n+1)(х) имеет хотя бы один нуль. Т.е. существует g=g(х'): φ(n+1)(g)=0. Из равенства (1) получим:
Отсюда, Т.к. х' выбрано произвольно, то последнее равенство верно при
Свойства разделенных разностей Пусть задана дискретная функция f(х) в узлах х0...хn (хk < хk+1), а также её разделенная разность k-ого порядка:
Лемма: Справедливо равенство: Доказательство (методом математической индукции): При k=1: Пусть верность равенства доказана при Докажем для m-ого порядка:
Рассмотрим слагаемое для f(х1):
Аналогично для остальных слагаемых. Что и требовалось доказать.
Числа αk. Пусть хi<хi+1 при Обозначим:
Данные числа обладают следующими свойствами: 1. 2. 1) 2) Умножим на (-1)n-i. Тогда знак числителя не зависит от i, значит знак каждого слагаемого такой же, отсюда, αi>0. 3. Действительно:
Из ранее доказанной Леммы:
Что и требовалось доказать.
Задача Чебышева. Разрешимость системы Пусть f(х) задана дискретно в узлах х0...хn+1 значениями у0...уn+1 соответственно (хi<xi+1). Требуется построить многочлен Рn(x), наилучшим образом аппроксимирующий в узлах значения функции. Задача Чебышева. Обозначим: Рn(x)=Pn(x,A), где А=(а0, а1...аn). Необходимо определить μ=inf max |Pn(xk)-yk| и минимизирующий многочлен Pn(x,A), если он существует. Задачи такого типа называют минимальными. Предварительно рассмотрим систему:
В системе n+2 неизвестных: h, а0, а1...аn. Докажем, что определитель системы Δ≠0.
а) sgn Δ0=sgn Δ1 Действительно, рассмотрим функцию q0(x):
в х2, х3...хn+1 Отсюда, sgn q0(x0)=sgn q0(x1), т.к. точки б) sgn Δ1 = sgn Δ2 Рассмотрим следующую функцию:
в х0, х3...хn+1 Отсюда, sgn q1(x1)=sgn q1(x2). И т.д. Таким образом, получим: Δ≠0, следовательно, решение системы существует. Обозначим его как Pn(x,A*).
Теорема Чебышева Решение задачи Чебышева: Определить: минимизирующий многочлен Pn(x,A), если он существует. Теорема: Такой многочлен сущестует и совпадает с решением системы
Доказательство Не ограничивая общности будем считать, что Если это не так, рассмотрим функцию -f(х) в системе все уравнения умножим на (-1), тогда решением будет многочлен –Pn(x,A*). Перепишем систему следующим образом:
Воспользуемся свойствами чисел αk:
При этом:
Однако μ>h, т.к. иначе получим h<h. Значит, μ=h. И для всякого k максимум разницы между Pn(x) и f(x) не может быть меньше.
Далее нетрудно доказать, что многочлены Pn(x,A*) и Pn(x,A0) равны. Что и требовалось доказать.
Замечание Можно рассмотреть континуальный аналог задачи Чебышева. Необходимо найти для Этот многочлен есть решение дискретной задачи при некотором наборе узлов.
Многочлены Чебышева Постановка задачи: Для многочленов Pn(x,A) степени n co старшим коэффициентом, равным 1, требуется определить для Таким образом, рассматривается задача о многочленах со старшим коэффициентом, равным 1, наименее отклоняющихся от нуля.
Рассмотрим многочлены Чебышева:
Теорема Tn(x) – многочлены степени n со старшим коэффициентом, равным 1, методом математической индукции. Доказательство При n=1:
При n=2:
Пусть утверждение верно
Что и требовалось доказать.
Теорема (свойство четности) Все многочлены T2n(x) являются четными функциями, а T2n+1(x) – нечетными. Доказательство При n = 0: T0=1 – четная функция; T1=x – нечетная. Пусть утверждение верно Заметим, что из предположения T2k-1 – нечетная функция, T2k-2 – четная. Тогда а Что и требовалось доказать.
Нули многочленов Чебышева Заметим, что:
Обозначим Тогда Т.к.
Экстремумы. Рассмотрим локальные экстремумы Тn(x) на [-1;1]. Т.к. Следовательно, cos(n·arccosx) = ±1 n·arccosx = πk,
Обозначим Отсюда, Т.к.
Ортогональность с весом Функции f(x) и g(x) ортогональны на [a;b] с весом ρ(x), если Доказательство Обозначим
Что и требовалось доказать. Лемма Tn(x) – многочлены со старшим коэффициентом равным еденице, наименее отклоняющиеся от нуля на [-1;1]. Т.е. если Pn(x) – многочлен степени n со старшим коэффициентом равным единице, то:
Доказательство Предположим противное:
Обозначим как Qn(x) = Tn(x)-Pn(x). Заметим, что многочлен Qn(x): 1)имеет (n-1) степень
Таким образом, получено, что между каждыми двумя точками Противоречие доказывает требуемое.
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 324; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.148.105.127 (0.01 с.) |

 ). А также заданы значения в узлах для производных функции f(х):
). А также заданы значения в узлах для производных функции f(х): ; S=0, 1...Sk-1. Причем
; S=0, 1...Sk-1. Причем 

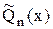 n-ой степени:
n-ой степени: удовлетворяет условиям вышеописанной системы. Тогда их разность
удовлетворяет условиям вышеописанной системы. Тогда их разность  удовлетворяет следующим условиям:
удовлетворяет следующим условиям:

 (1)
(1)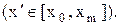

 Тогда при таком выборе К
Тогда при таком выборе К  и обращается в ноль в (n+2) точках (считая кратность): х0...хm, х'.
и обращается в ноль в (n+2) точках (считая кратность): х0...хm, х'.






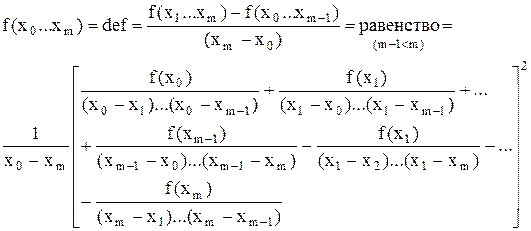



 - очевидно
- очевидно Действительно, т.к.
Действительно, т.к.




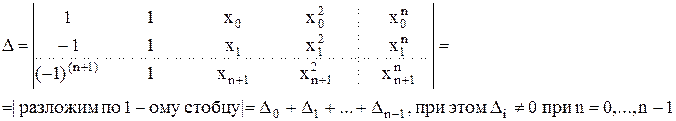 Заметим, что:
Заметим, что: - многочлен n-ого порядка с нулями
- многочлен n-ого порядка с нулями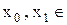 промежутку знакопостоянства функции.
промежутку знакопостоянства функции. - многочлен n-ого порядка с нулями
- многочлен n-ого порядка с нулями
 т.е. Pn(x,A)=Pn(x,A*).
т.е. Pn(x,A)=Pn(x,A*).
 .
.
 .
. и минимизирующий многочлен Pn(x,A0), если он существует.
и минимизирующий многочлен Pn(x,A0), если он существует. и минимизирующий многочлен Pn(x,Amin), если это возможно.
и минимизирующий многочлен Pn(x,Amin), если это возможно.
 - многочлен 1ой степени.
- многочлен 1ой степени.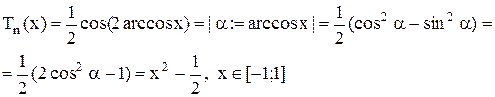
 . Докажем для n = k.
. Докажем для n = k. Заметим, что Tk-1(x) – многочлен степени k-1 по предположению, Tk-2(x) – многочлен степени (k-2). Таким образом, Tk(x) – многочлен степени k со старшим коэффициентом, равным 1.
Заметим, что Tk-1(x) – многочлен степени k-1 по предположению, Tk-2(x) – многочлен степени (k-2). Таким образом, Tk(x) – многочлен степени k со старшим коэффициентом, равным 1. - четная функция,
- четная функция, - нечетная.
- нечетная. .
. .
. .
. .
. - нули многочлена Чебышева Tn(x) на [-1;1].
- нули многочлена Чебышева Tn(x) на [-1;1]. При этом других нулей нет (т.к. многочлен nой степени имеет не более n нулей).
При этом других нулей нет (т.к. многочлен nой степени имеет не более n нулей). то точками экстремума для Тn(х) на [-1;1] будут точки, где
то точками экстремума для Тn(х) на [-1;1] будут точки, где 

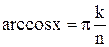
 где
где 
 .
.
 - экстреальные точки для Tn(x) на [-1;1].
- экстреальные точки для Tn(x) на [-1;1].
 (ортогональность в смысле Гильбертова пространства L2 [a;b]).
(ортогональность в смысле Гильбертова пространства L2 [a;b]).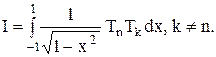


 .
. 2)
2)  , т.к. из предположения.
, т.к. из предположения.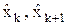 многочлен Qn(x) меняет свой знак. Т.е. многочлен Qn(x), отличный от нуля (т.к. он ≠0 в точках
многочлен Qn(x) меняет свой знак. Т.е. многочлен Qn(x), отличный от нуля (т.к. он ≠0 в точках  ) имеет n нулей, а значит Qn(x)≡0.
) имеет n нулей, а значит Qn(x)≡0.


