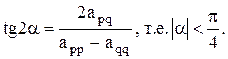Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Максимизация первого столбцаСодержание книги Поиск на нашем сайте Рассмотрим матрицу B=AUp=(bij). В ней: b1 = ca1+sap, bp = -sa1+cap. Остальные столбцы совпадают со столбцами А.
Свойство 1 Доказательство Действительно:
Отсюда Что и требовалось доказать.
Выберем угол α в матрице Up так, чтобы | b1 | был максимален. Рассмотрим функцию Тогда Обозначим α=αp: f ’(α)=0. Будем выбирать αp по правилу: а) если б) иначе αp находится из равенства в) заметим, что αp=0 тогда и только тогда, когда
Свойство 2 Если | a1|≥| ap|, то | b1|≥| a1|≥| ap|≥| bp| и | b1|>| a1| при Доказательство Действительно: 1) Пусть Следовательно, из определения f(α): Отсюда:
и | b1|>| a1| при 2) Пусть Рассмотрим функцию Т.к. f ’’(αp)≤0, т.е. αp – локальный максимум ( Следовательно, Что и требовалось доказать.
Свойство 3 Если | a1|≥| ap|, то Доказательство Действительно:
Что и требовалось доказать. Алгоритм сингулярного разложения Пусть дана матрица A=(aij). Рассмотрим матрицу A1=AU1, где U1 – ортогональная матрица перестановки столбцов: первый столбец матрицы А1 максимален. Рассмотрим последовательность матриц: Ak+1=AkUp(k), k=1,2…, где p(k) – номер столбца (= 2,3..n; 2,3..); Up(k) – матрица простейшего поворота: u11 = up(k)p(k)= c =cosα, -up(k)1 = u1p(k)= -s = - sinα, остальные диагональные элементы равны 1, а недиагональные – нулю. Т.е. у всех Ak первый столбец максимальный, у всех Ak+1 первый столбец ортогонален p(k+1). При этом сумма квадратов сохраняется. Обозначим Отсюда следует лемма: Лемма 1 Последовательность норм Доказательство По Свойству 2 предыдущего пункта последовательность не убывает. А из сохранения суммы квадратов она ограничена, а значит сходится.
Замечание Отсюда не следует сходимость векторов
Лемма 2 Последовательность матриц {Ak} сходится поэлементно при k→∞ (без доказательства). Т.е. 1)первый столбец наибольший по модулю 2)первый столбец ортогонален всем остальным. Действительно, предположим противное Таким образом, получен алгоритм сингулярного разложения. Пусть матрица А nого порядка. Построим последовательность Ak→A∞. 1. Обозначим как 2. Максимизируем второй столбец матрицы с помощью последующих, не изменяя первый. Полученная последовательность матриц сходится к некоторой матрице 3. И т.д. n-1. Максимизируем (n-1)ый столбец у матрицы Запишем полученную матрицу в виде: Обозначим нормы столбцов матрицы Получим Таким образом, AV = WS, т.е. A = WSVT – SVD-разложение.
Главное собственное число
Пусть А=(aij) – симметричная матрица. Метод максимизации столбцов дает следующее:
Перемножим равенства:
максимальное собственное число матрицы A2 (из метода максимизации). λ=±b – главное собственное число симметричной матрицы А.
Метод вращения Рассмотрим симметричную матрицу А=(аij). Обозначим ортогональную матрицу вращения Upq(α): uqq = upp= c =cosα, -upq = uqp= -s = - sinα, остальные диагональные элементы равны 1, а недиагональные – нулю. Рассморим вращение матрицы в плоскости Opq:
Матрица В=AUpq отличается от А столбцами bp и bq: bp=c·ap+s·aq bq= -s·ap+c·aq bj=aj, j≠p,q Матрица dpj=c·bpj+s·bqj dqj= -s·bpj+c·bqj Остальные строки не изменяют. Тогда, Разобьем S на диагональную и недиагональную части:
Заметим: При элементарном вращении D недиагональные элементы аpi, aqi и аip, aiq (i≠p,q) меняются так, что попарные суммы квадратов их модулей сохраняются. Кроме этих элементов вне диагонали меняется элемент аpq. Т.е. величина S2 меняется при элементарном вращении настолько, насколько изменится |apq|2. Будем подбирать вращения так, чтобы S2 максимально уменьшалась. Положим dpq=0: dpq=c·bpq+s·bqq=c(-s·app+c·apq)+s(-s·aq p+c·aqq)= α выберем следующим образом: 1) при аpp cos2α=0 => α=π/4 2) иначе
|
||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 406; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |



 .
.
 .
. , то
, то 

 .
. .
.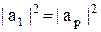 .
. .
.
 .
. .
. ,
,  , a
, a  , то
, то ) и общий максимум функции на
) и общий максимум функции на 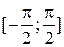 .
. .
. , т.е. новые столбцы ортогональны.
, т.е. новые столбцы ортогональны.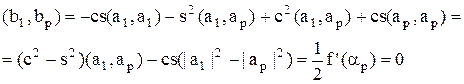
 . Действительно, тогда
. Действительно, тогда  .
. первых столбцов матриц сходится.
первых столбцов матриц сходится.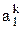 .
. . Эта матрица обладает следующими свойствами:
. Эта матрица обладает следующими свойствами: . Умножим на Up1, получим требуемое.
. Умножим на Up1, получим требуемое. в процессе максимализации первого столбца. Т.о. первый столбец макимален и ортогонален всем остальлным.
в процессе максимализации первого столбца. Т.о. первый столбец макимален и ортогонален всем остальлным. .
.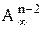 . Получим матрицу
. Получим матрицу  с монотонными нормами и взаимоортогональными столбцами.
с монотонными нормами и взаимоортогональными столбцами. , где ортогональная матрица V есть произведение ортогональных матриц.
, где ортогональная матрица V есть произведение ортогональных матриц. , где W – ортогональная матрица.
, где W – ортогональная матрица.


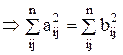
 отличается от В р-ой и q-ой строками:
отличается от В р-ой и q-ой строками: