
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вариационное свойство собственных значенийСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Матрица А неотрицательно определена, если Лемма Собственные числа неотрицательно определенной матрицы неотрицательны. Доказательство Пусть А – неотрицательно определенная матрица, λ1 – её собственное число. Тогда Т.к. Что и требовалось доказать. Матрица А симметричная, если Лемма 1 Если А симметрична, неотрицательно определена и (Ay,y)=0, то Ay=0. Геометрически: А не может сделать вектор у ортогональным самому себе, а может лишь обратить его в ноль. Доказательство Рассмотрим выражение (A(y+tz),y+tz), где z – произвольный вектор; t – вещественное, малое число (t<<1).
Если бы (Ay,z)≠0, то знак всего выражения можно было бы сделать отрицательным, выбирая знак t, что противоречило бы условию неотрицательной определенности А. Значит, (Ay,z)=0. Т.к. элеент z выбирался произвольно, то Ay=0. Что и требовалось доказать.
Рассмотрим выражение: Функция n переменных F(y)=(Ay,y) непрерывна на единичной сфере
Лемма 2 (вариационное свойство) Если А – симметричная матрица, то Доказательство Из приведенных выше рассуждений Т.к. Получим: Из выбора точку y’ верно: (Ay,y)≤λ1 для любого вектора y из S1. Т.е. Следовательно, из (*), используя Лемму 1, получим:
Что и требовалось доказать.
Приведение симметричной матрицы к диагональному виду Из теорем алгебры: Любое собственное число λ произвольной матрицы А равно скалярному произведению (Ax,x), где x – некоторый вектор: || x ||=1.
Первый шаг Пусть λ1 – максимальное собственное число матрицы А, т.е. Обозначим как y1 – собственный вектор матрицы А, отвечающий λ1: || y1 ||=1. Второй шаг Обозначим как Ln-1 – подпространство, ортогональное подпространству, образованному вектором y1 (т.к. dim {y1}=1, то dim Ln-1=n-1).
Очевидно, что Ln-1 инвариантное подпространство для А (т.е. если Действительно, пусть Обозначим
Т.о. y2 – собственный вектор матрицы А, ортогональный y1.
Третий шаг Будем рассматривать далее подпространство
В итоге получим набор собственных векторов матрицы А {yk}: || yk ||=1, ортогональных друг другу, соответствующих собственным числам {λk}. Обозначим матрицу собственных векторов как:
Получим систему: Очевидно, что У – ортогональная матрица, т.к. ее столбцы нормированны и ортогональны друг другу. Тогда запишем систему в виде: YTAY=diag(λ1… λn) или A=Ydiag(λ1… λn)YT. Геометрически это означает, что: Всякая симметричная матрица может быть приведена к диагональному виду, т.е. в некотором базисе соответствующий оператор представляется диагональной матрицей, а значит его действие состоит в растягивании на величину λк соответствующего базисного вектора. Базис состоит из собственных векторов, т.е. диагональная матрица нетривиальна.
Сингулярное разложение матрицы Пусть А – вещественная матрица. Тогда AAT, ATA – симметричные матрицы, а значит они могут быть приведены к диагональному виду. Обозначим AAT=UЛUT, ATA=VЛVT, где U,V – ортогональные матрицы, Л – диагональная.
Лемма Собственные числа матриц AAT, ATA равны и неотрицательны. Доказательство 1. Пусть λi – некоторое собственное число матрицы ATA. Тогда
2. Обозначим
Таким образом матрицы Л для AAT, ATA совпадают. Что и требовалось доказать.
Заметим, что если матрица А невырожденная, то её собственные числа больше нуля.
Обозначим как
Обратная к Обозначим
Таким образом, получено: Умножим
Для всякой вещественной матрицы А существует её сингулярное разложение, т.е. представление в виде: A=USW, где U,W – ортогональные матрицы, S=diag(s1..sn), si≥0, i=1..n.
Задача: Доказать, что
Сопряженная матрица Рассмотрим вещественную матрицу A=(aij). Тогда сопряженная к ней в пространстве Rn матрица: A*=(a*ij)=AT. В пространстве Rn A – линейный оператор; А* - сопряженный к нему. Образ Im A – область значений оператора А: Im A= A(Rn). Ядро ker A – множество элементов, обращаемых оператором А в ноль:
ker A={x | Ax=0}. Im A, ker A – подпространства пространства Rn. Задача: доказать указанное выше утверждение.
Лемма Доказательство Im A – подпространство пространства Rn. Обозначим как L его ортогональное дополнение (множество всех элементов из Rn, ортогональных каждому элементу из Im A). Тогда
Т.е. Что и требовалось доказать.
Частная спектральная задача Частная спектральная задача – задача нахождения некоторых собственных чисел матрицы и соответствующих собственных векторов.
Вариационный метод Пусть А – симметричная матрица. Найдем её максимальное собственное число. Т.к. из ранее доказанного Степенной метод Для матрицы А предположим, что: а) её собственные вектора φ1… φn образуют базис в Rn. б) её собственные числа удовлетворяют неравенствам | λ1 |>| λk|, k=2..n. Тогда всякий вектор х из Rn может быть представим в виде: Построим последовательность векторов: x(1)=Ax, x(2)=Ax(1)…x(m)=Ax(m-1)=Amx. Значит,
т.к. тогда Получим, что:
а (т.к. он определяется с точностью до скалярного множителя). Знак λ1 найдем из следующего равенства:
Точность метода:
Метод максимизации столбцов Пусть A=(akp) – вещственная, квадратная матрица порядка n. Обозначим как ap – pый столбец матрицы. Заметим, что
Рассмотрим матрицу простого поворота Up: u11 = upp= c =cosα, -up1 = u1p= -s = - sinα, остальные диагональные элементы равны 1, а недиагональные – нулю. Из ранее доказанного матрица Up осуществляет поворот на угол α против часовой стрелки.
|
||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 623; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.181.93 (0.011 с.) |

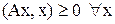 .
. .
.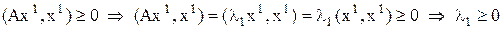 .
. .
.
 .
. . Следовательно, по первой теореме Вейерштрасса F(y) достигает на S1 своих точных граней. Это означает, что
. Следовательно, по первой теореме Вейерштрасса F(y) достигает на S1 своих точных граней. Это означает, что  .
.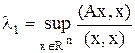 - собственное число матрицы А.
- собственное число матрицы А. .
. , то || y ||=1, а значит
, то || y ||=1, а значит 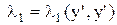 .
. . (*)
. (*) Последнее утверждение верно и для любого вектора x из пространства Rn. Т.е.
Последнее утверждение верно и для любого вектора x из пространства Rn. Т.е.  - неотрицательно определенная матрица.
- неотрицательно определенная матрица. , т.е. λ1 – собственное число матрицы А.
, т.е. λ1 – собственное число матрицы А.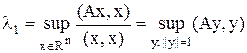 .
.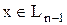 , то
, то  ).
).
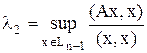 . Тогда из Леммы 2:
. Тогда из Леммы 2: .
. , повторим указанные в шаге два рассуждения.
, повторим указанные в шаге два рассуждения.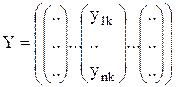 .
. Y.
Y. . Умножим скалярно равенство на xi:
. Умножим скалярно равенство на xi: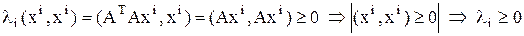
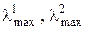 собственные числа матриц ATA, AAT соответственно.
собственные числа матриц ATA, AAT соответственно.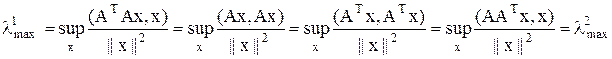
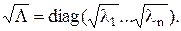 Тогда:
Тогда: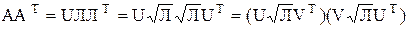 .
. матрица имеет вид:
матрица имеет вид: 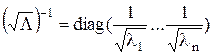 .
. . Тогда:
. Тогда: .
. .
. на B-1 справа:
на B-1 справа:  .
. - сингулярное разложение матрицы А.
- сингулярное разложение матрицы А. .
. . Докажем, что L=ker A.
. Докажем, что L=ker A.
 Т.е.
Т.е.  .
.
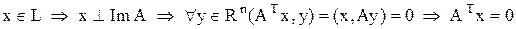
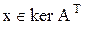 .
.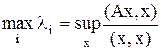 , то задача сводится к нахождению стационарных точек функционала
, то задача сводится к нахождению стационарных точек функционала  .
. .
. . Преобразуем правую часть равенства:
. Преобразуем правую часть равенства: при m>>1,
при m>>1,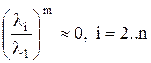 .
. ,
, - соответствующий собственный вектор
- соответствующий собственный вектор - знак находится по первой компоненте.
- знак находится по первой компоненте. .
. ;
; 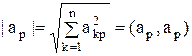 .
.


