
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод Монте-Карло (метод статистических испытаний)Содержание книги
Поиск на нашем сайте
Всякий интеграл
Из теории вероятностей: 1) случайная величина ξ равномерно распределена на [0;1], если 2) двумерная случайная величина (ξ,η) равномерно распределена на [0;1]×[0;1], если
В ЭВМ существует датчик псевдослучайных чисел, значениями которого являются случайные числа, равномерно распределенные на [0;1].
Алгоритм: 1) генерируются равномерно распределенные на [0;1] случайные числа ξk, ηk 2) вычисляется f(ξk) 3) сравнивается f(ξk) и ηk и подсчитывается число N неравенств f(ξk) > ηk, k=1..M. При достаточно большом числе испытаний M>>1 Ответ, полученный с помощью данного метода носит вероятностный характер и может сколь угодно сильно отличаться от точного значения интеграла. Однако с вероятностью 99,7% ошибка не превосходит
Правило Рунге практической оценки погрешности Величины погрешности численного интегрирования зависит как от шага h, так и от гладкости подинтегральной функции. Если величина погрешности велика, то ее можно уменьшить путем измельчения сетки на данном отрезке [xk-1;xk]. Для этого необходимо уметь апостериорно (т.е. после проведения расчета) оценивать погрешность. Правило Рунге позволяет произвести такую оценку. Представим интеграл в виде приближенной формулы:
Заметим, что S и R зависят от шага h, т.е. от числа точек разбиения n. Тогда S=Sn, R=Rn. Будем считать, что дана априорная погрешность (предполагаемая):
Если С известно, то можно заранее для нужной точности указать число точек разбиения и т.п. Если же С неизвестно, то используют правило Рунге: 1. Производят 2 вычисления приближенного значения интеграла при n=n1 и n=n2 (обычно n2=2n1). 2. Таким образом, будет получено: I=Sn1+Rn1; I=Sn2+Rn2 Вычитая из первого равенства второе, получим:
Подставим C в Rn1 и Rn2:
При этом выражение Таким образом,
Это и есть правило Рунге: В выбранной квадратурной формуле берется некоторое число точек разбиения n1 и вычисляетя соответствующее ему значение интеграла. Затем вычисляется приближенное значение, соответствующее числу точек разбиения n2>n1. Если модуль разности между ними не превышает требуемой точности, то вычисления останавливаются. В противном случае, процедуру необходимо повторить. В качестве ответа обычно берут Sn2 или линейную комбинацию Sn1, Sn2.
Глава4. Алгебраическая проблема собсвенных значений Постановка задачи Пусть A=(aik) – вещественная матрица порядка n×n пространства Rn. Элементы пространства Rn имеют вид: x=(x1..xn)T. Скалярное произведение векторов в Rn: Норма вектора в пространстве Rn:
Число λ – собственное число матрицы А, если существует нетривиальный вектор x1≠0: Ax=λx. При этом x1 – собственный вектор А. (1) Множество всех собственных чисел матрицы – её спектр.
Спектральная задача – задача нахождения всех или нескольких собственных чисел матрицы и, возможно, соответствующих им собственных векторов.
Пусть λ1 – собственное число матрицы А. Перепишем уравнение (1) в виде:
Многочлен вида: Т.о. если λ – собственное число матрицы А, то λ – корень характеристического многочлена матрицы А. Верно и обратное.
Утверждение Любая матрица А порядка n×n имеет хотя бы один собственный вектор и имеет n собственных чисел (могут быть как различными, так и кратными).
Из сказанного: задача нахождения собственных чисел матрицы А сводится к задаче нахождения корней её характеристического многочлена, т.е. решения уравнения Pn(λ) = 0.
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 306; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.156.84 (0.01 с.) |

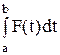 можетбыть сведен линейной заменой масштабов к интегралу вида
можетбыть сведен линейной заменой масштабов к интегралу вида  , где 0≤f(x)≤1.
, где 0≤f(x)≤1.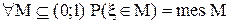 . В частности
. В частности  .
. . При этом если ξ,η равномерно распределены на [0;1], то (ξ,η) равномерно распределена на [0;1]×[0;1].
. При этом если ξ,η равномерно распределены на [0;1], то (ξ,η) равномерно распределена на [0;1]×[0;1]. Таким образом, для вычисления интеграла
Таким образом, для вычисления интеграла  .
.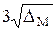 (
(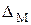 - дисперсия от среднеарифметического). При реальных испытаниях ошибка обычно не превосходит
- дисперсия от среднеарифметического). При реальных испытаниях ошибка обычно не превосходит  . С увеличением числа испытаний погрешность ответа будет убывать римерно как
. С увеличением числа испытаний погрешность ответа будет убывать римерно как  .
.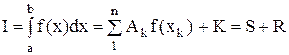
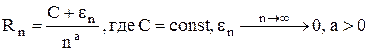
 Отсюда,
Отсюда,  .
.

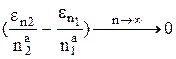 .
. , т.к.
, т.к.  невелико (обычно
невелико (обычно  , а=2).
, а=2).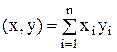 .
. .
. .
.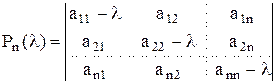 - характеристический многочлен матрицы А.
- характеристический многочлен матрицы А.


