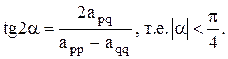Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава1. Проблема аппроксимацииСодержание книги Поиск на нашем сайте Глава1. Проблема аппроксимации
Полиномиальная апппроксимация Постановка задачи Из теорем математического анализа известно, что всякая непрерывная на отрезке [a;b] функция f(x) может быть хорошо приближена полиномом Pn(x). Теорема Вейерштрасса: Однако эта теорема не дает ответа на вопрос о существовании хорошего интерполяционного полинома для заданного множества точек {(xi, yi)}.
Пусть функция f(x) известна только в узлах некоторой сетки xi, т.е. задана таблицей: (xk≤xk+1)
Задача нахождения значений функции: a) между узлами ( б) вне узлов ( Теорема: Для всякой дискретной функции f(x), заданной предыдущей таблицей существует многочлен Pn(x) степени n, совпадающий в узлах с этой функцией (Pn(xk)=yk Доказательство Будем искать этот полином в виде: Pn(x)=a0+a1x+..+anxn. Запишем условие (1) в виде системы:
Будем считать, что все узлы – разные, т.е xk< xk+1. В данной системе неизвестные – ak. Определитель системы – отличный от нуля определитель Вандермонда:
Т.о. решение системы (2) существует, а значит существует многочлен Pn(x). Докажем его единственность. Предположим противное: существует Qn(x):
Определение Полином Pn(x) – интеполяционный полином для функции f(x).
Рассмотрим на [-1;1] ее интерполяционный многочлен (для значений по равномерным узлам): Pn(xk)= C возрастанием n многочлен также возрастает, увеличивая аксиляции колебаний.
Интерполяционный полином в форме Лагранжа Из системы (2) получим систему следующего вида:
Будем считать неизвестными a0,a1..an, -1. Полученная система имеет (n+1) порядок. Ее нетривиальное решение из предыдущей теоремы существует, следовательно, ее определитель равен 0 (иначе решение (3) было бы нулевым). Разложим этот определитель по последнему столбцу:
где
Перпишем последнее равенство в виде:
Заметим, что: 1) 2) 3) Следовательно, многочлен
Рассмотрим следующий многочлен (n+1)ой степени: Обозначим Заметим, что:
Т.о.
Погрешность интерполяции Представим функцию f(x) в виде: f(x)=Pn(x)+Rn(x), где Rn(x) – погрешность интерполяции. Заметим, что Rn(x) зависит от свойств f(x) (так если f(x) линейна, то Rn(x)≡0 при n>2). Будем считать априорно, что Запишем погрешность в виде: Rn(x)=kωn+1(x)+φ(x). Тогда φ(x)=f(x)-Pn(x)- kωn+1(x) и φ(xk)=0, Выберем k из условия φ(x’)=0, где x’ – точка, в которой оценивается погрешность: Из уравнения φ(x’)=0 получим: При таком выборе k φ(x’) Тогда по т. Ролля По т. Ролля Т.о. из (4) получим:
Тогда
Интерполяционный полином в форме Ньютона Рассматривается функция f(х), заданная дискретно в узлах х0...хn. Ставится задача её аппроксимации по этим данным. Введём понятие разделённых разностей: 1-ого порядка - 2-ого порядка - k-ого порядка - нулевого порядка -
Тогда:
....................
....................
Из первого равенства получим:
Обозначим все слагаемые, кроме последнего как Рn(х), последнее - Rn(х). Рn(х) – интерполяционный полином (т.к. он порядка n и совпадает в узлах с f(х)) Ньютона.
Следствие: Аппроксимация сплайнами Рассматривается задача приближения функции f(х) на некотором интервале по её значениям в узлах х0...хn (хk< хk+1
Обозначим разбиение {x0…xn} как Т.
Сплайн 1) на каждом из отрезков [xk-1, xk] 2) в узлах совпадает с функцией f(х): 3) во внутренних узлах (х1...хn-1) эта функция непрерывна вместе со своими производными до (m-1)-ого порядка
Построение сплайна Обозначим многочлен, который необходимо найти на [xk-1, xk] как:
Из условия 2) для сплайна => (n+1) уравнение. Из условия 3) => (n-1) уравнение для каждой из m функций. Итого всего уравнений для сплайна: n+1+m(n-1)=n(m+1)+1-m Всего неизвестных коэффициентов (m+1) для каждого из n отрезков, т.е. n(m+1). Таким образом, число уравнений и искомых коэффициентов совпадает при m=1, иначе условий не хватает для нахождения коэффициентов, и требуются дополнительные условия.
Основные сплайны: - 1-ого порядка – линейные; - 2-ого порядка – кубические (m=3). Для них 4n-2 уравнения и 4n коэффициентов. В качестве двух дополнительных условий обычно задают значения производных в двух узлах. Таким образом, функция f(х) может быть интерполирована на [x0, xn] сплайном заданного порядка.
Метод наименьших квадратов Рассмотрим некоторую функцию Таким образом, функцию f(х) на [a,b], заданную в узлах х0...хn можно аппроксимировать некоторыми функциями φk(k), общее число которых (р+1), р≠n. Рассмотрим некоторые употребляемые частные случаи: 1) Полиномиальная задача: найти для функции f(х) такую линейную комбинацию функций φk: Рассмотрим следующее выражение:
Необходимое условие минимума функции
Таким образом, получим следующую систему уравнений:
Или:
2) Континуальная задача: аппроксимировать функцию f(х) в С [a, b] в смысле средне квадратичного. Обозначим Необходимое условие экстремума имеет вид:
Получим систему:
Или:
т.к.
Определитель с матрицей А=(аkm), где аkm= (φk, φm) – определитель Грамма.
Заметим, что det А≠0, если система Рассмотрим подпространство
Погрешность интерполяции. Обозначим f(х):=Qn(х)+Rn(х). Представим погрешность Rn в виде:
Отсюда, где S=0...Sk-1; φ(хk)=0; k=0, 1...m (т.е. хk – нули кратности S0...Sm соответственно). Выберем k из условия φ(х')=0, где х' – точка, в которой оценивается погрешность Из уравнения φ(х')=0 получим:
Будем предполагать, что Следовательно, по Т. Ролля φ'(х) обращается в ноль в по крайней мере (n+1) точке. ........................................................................... Тогда, по Т. Ролля φ(n+1)(х) имеет хотя бы один нуль. Т.е. существует g=g(х'): φ(n+1)(g)=0. Из равенства (1) получим:
Отсюда, Т.к. х' выбрано произвольно, то последнее равенство верно при
Задача Чебышева. Обозначим: Рn(x)=Pn(x,A), где А=(а0, а1...аn). Необходимо определить μ=inf max |Pn(xk)-yk| и минимизирующий многочлен Pn(x,A), если он существует. Задачи такого типа называют минимальными. Предварительно рассмотрим систему:
В системе n+2 неизвестных: h, а0, а1...аn. Докажем, что определитель системы Δ≠0.
а) sgn Δ0=sgn Δ1 Действительно, рассмотрим функцию q0(x):
в х2, х3...хn+1 Отсюда, sgn q0(x0)=sgn q0(x1), т.к. точки б) sgn Δ1 = sgn Δ2 Рассмотрим следующую функцию:
в х0, х3...хn+1 Отсюда, sgn q1(x1)=sgn q1(x2). И т.д. Таким образом, получим: Δ≠0, следовательно, решение системы существует. Обозначим его как Pn(x,A*).
Теорема Чебышева Решение задачи Чебышева: Определить: минимизирующий многочлен Pn(x,A), если он существует. Теорема: Такой многочлен сущестует и совпадает с решением системы
Доказательство Не ограничивая общности будем считать, что Если это не так, рассмотрим функцию -f(х) в системе все уравнения умножим на (-1), тогда решением будет многочлен –Pn(x,A*). Перепишем систему следующим образом:
Воспользуемся свойствами чисел αk:
При этом:
Однако μ>h, т.к. иначе получим h<h. Значит, μ=h. И для всякого k максимум разницы между Pn(x) и f(x) не может быть меньше.
Далее нетрудно доказать, что многочлены Pn(x,A*) и Pn(x,A0) равны. Что и требовалось доказать.
Замечание Можно рассмотреть континуальный аналог задачи Чебышева. Необходимо найти для Этот многочлен есть решение дискретной задачи при некотором наборе узлов.
Многочлены Чебышева Постановка задачи: Для многочленов Pn(x,A) степени n co старшим коэффициентом, равным 1, требуется определить для Таким образом, рассматривается задача о многочленах со старшим коэффициентом, равным 1, наименее отклоняющихся от нуля.
Рассмотрим многочлены Чебышева:
Теорема Tn(x) – многочлены степени n со старшим коэффициентом, равным 1, методом математической индукции. Доказательство При n=1:
При n=2:
Пусть утверждение верно
Что и требовалось доказать.
Теорема (свойство четности) Все многочлены T2n(x) являются четными функциями, а T2n+1(x) – нечетными. Доказательство При n = 0: T0=1 – четная функция; T1=x – нечетная. Пусть утверждение верно Заметим, что из предположения T2k-1 – нечетная функция, T2k-2 – четная. Тогда а Что и требовалось доказать.
Нули многочленов Чебышева Заметим, что:
Обозначим Тогда Т.к.
Экстремумы. Рассмотрим локальные экстремумы Тn(x) на [-1;1]. Т.к. Следовательно, cos(n·arccosx) = ±1 n·arccosx = πk,
Обозначим Отсюда, Т.к.
Ортогональность с весом Функции f(x) и g(x) ортогональны на [a;b] с весом ρ(x), если Доказательство Обозначим
Что и требовалось доказать. Лемма Tn(x) – многочлены со старшим коэффициентом равным еденице, наименее отклоняющиеся от нуля на [-1;1]. Т.е. если Pn(x) – многочлен степени n со старшим коэффициентом равным единице, то:
Доказательство Предположим противное:
Обозначим как Qn(x) = Tn(x)-Pn(x). Заметим, что многочлен Qn(x): 1)имеет (n-1) степень
Таким образом, получено, что между каждыми двумя точками Противоречие доказывает требуемое.
Погрешность При численном дифференцировании приходится вычитать друг из друга близкие значения функции. Это приводит к уничтожению первых значащих цифр, т.е. к потере части достоверных знаков числа.
ρ определяет погрешность метода и неограниченно убывает при h→0. Но есть и неустранимая погрешность, связанная с погрешностью при вычислении функции f(x): Таким образом, полная погрешность не превосходит
Меньший шаг невыгоден, а меньшая погрешность недостихима. Эта минимальная ошибка тем меньше, чем меньше погрешность входных данных.
Ортогональные матрицы Ортогональные матрицы Рассмотрим два ортонормированных базиса в пространстве Rn: Разложим вектора второго базиса по векторам первого:
Обозначим как U=(uik). Рассмотрим скалярное произведение:
Таким образом, сумма Cik трактуется как произведение iой строки матрицы U на kый столбец матрицы UT. C другой стороны, из свойств ортонормированного базиса матрица C=(cik)=E. Отсюда получим: UUT=E или UTU=E.
Из выведенных формул следуют равенства: 1) U-1 = UT (из определения обратной матрицы) 2) (Ux,Uy) = (x,y) для любых векторов x,y из Rn (т.е. скалярные произведения векторов и их образов относительно U совпадают). Действительно, (Ux,Uy) = (UUTx,y) = (x,y) 3) Отсюда в частности следует: || x || = || Ux || Действительно,
Матрица V, удовлетворяющая любому из этих трех равенств, ортогональная. Она обладает следующими свойствами: 1) переводит ортогональный базис в ортонормиррованный 2) сохраняет углы между векторами, а также их нормы
Первый шаг Пусть λ1 – максимальное собственное число матрицы А, т.е. Обозначим как y1 – собственный вектор матрицы А, отвечающий λ1: || y1 ||=1. Второй шаг Обозначим как Ln-1 – подпространство, ортогональное подпространству, образованному вектором y1 (т.к. dim {y1}=1, то dim Ln-1=n-1).
Очевидно, что Ln-1 инвариантное подпространство для А (т.е. если Действительно, пусть Обозначим
Т.о. y2 – собственный вектор матрицы А, ортогональный y1.
Третий шаг Будем рассматривать далее подпространство
В итоге получим набор собственных векторов матрицы А {yk}: || yk ||=1, ортогональных друг другу, соответствующих собственным числам {λk}. Обозначим матрицу собственных векторов как:
Получим систему: Очевидно, что У – ортогональная матрица, т.к. ее столбцы нормированны и ортогональны друг другу. Тогда запишем систему в виде: YTAY=diag(λ1… λn) или A=Ydiag(λ1… λn)YT. Геометрически это означает, что: Всякая симметричная матрица может быть приведена к диагональному виду, т.е. в некотором базисе соответствующий оператор представляется диагональной матрицей, а значит его действие состоит в растягивании на величину λк соответствующего базисного вектора. Базис состоит из собственных векторов, т.е. диагональная матрица нетривиальна.
Сопряженная матрица Рассмотрим вещественную матрицу A=(aij). Тогда сопряженная к ней в пространстве Rn матрица: A*=(a*ij)=AT. В пространстве Rn A – линейный оператор; А* - сопряженный к нему. Образ Im A – область значений оператора А: Im A= A(Rn). Ядро ker A – множество элементов, обращаемых оператором А в ноль: ker A={x | Ax=0}. Im A, ker A – подпространства пространства Rn. Задача: доказать указанное выше утверждение.
Лемма Доказательство Im A – подпространство пространства Rn. Обозначим как L его ортогональное дополнение (множество всех элементов из Rn, ортогональных каждому элементу из Im A). Тогда
Т.е. Что и требовалось доказать.
Частная спектральная задача Частная спектральная задача – задача нахождения некоторых собственных чисел матрицы и соответствующих собственных векторов.
Вариационный метод Пусть А – симметричная матрица. Найдем её максимальное собственное число. Т.к. из ранее доказанного Степенной метод Для матрицы А предположим, что: а) её собственные вектора φ1… φn образуют базис в Rn. б) её собственные числа удовлетворяют неравенствам | λ1 |>| λk|, k=2..n. Тогда всякий вектор х из Rn может быть представим в виде: Построим последовательность векторов: x(1)=Ax, x(2)=Ax(1)…x(m)=Ax(m-1)=Amx. Значит,
т.к. тогда Получим, что:
а (т.к. он определяется с точностью до скалярного множителя). Знак λ1 найдем из следующего равенства:
Точность метода:
Метод максимизации столбцов Пусть A=(akp) – вещственная, квадратная матрица порядка n. Обозначим как ap – pый столбец матрицы. Заметим, что
Рассмотрим матрицу простого поворота Up: u11 = upp= c =cosα, -up1 = u1p= -s = - sinα, остальные диагональные элементы равны 1, а недиагональные – нулю. Из ранее доказанного матрица Up осуществляет поворот на угол α против часовой стрелки.
Главное собственное число
Пусть А=(aij) – симметричная матрица. Метод максимизации столбцов дает следующее:
Перемножим равенства:
максимальное собственное число матрицы A2 (из метода максимизации). λ=±b – главное собственное число симметричной матрицы А.
Метод вращения Рассмотрим симметричную матрицу А=(аij). Обозначим ортогональную матрицу вращения Upq(α): uqq = upp= c =cosα, -upq = uqp= -s = - sinα, остальные диагональные элементы равны 1, а недиагональные – нулю. Рассморим вращение матрицы в плоскости Opq:
Матрица В=AUpq отличается от А столбцами bp и bq: bp=c·ap+s·aq bq= -s·ap+c·aq bj=aj, j≠p,q Матрица dpj=c·bpj+s·bqj dqj= -s·bpj+c·bqj Остальные строки не изменяют. Тогда, Разобьем S на диагональную и недиагональную части:
Заметим: При элементарном вращении D недиагональные элементы аpi, aqi и аip, aiq (i≠p,q) меняются так, что попарные суммы квадратов их модулей сохраняются. Кроме этих элементов вне диагонали меняется элемент аpq. Т.е. величина S2 меняется при элементарном вращении настолько, насколько изменится |apq|2. Будем подбирать вращения так, чтобы S2 максимально уменьшалась. Положим dpq=0: dpq=c·bpq+s·bqq=c(-s·app+c·apq)+s(-s·aq p+c·aqq)= α выберем следующим образом: 1) при аpp cos2α=0 => α=π/4 2) иначе
Глава1. Проблема аппроксимации
|
||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 611; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.014 с.) |


 ) – задача интерполяции
) – задача интерполяции ) – задача экстраполяции
) – задача экстраполяции ) и он единственен. (1)
) и он единственен. (1) (2)
(2)
 . Тогда полином Pn(x)-Qn(x) равен 0 в (n+1) точке
. Тогда полином Pn(x)-Qn(x) равен 0 в (n+1) точке  Pn(x)-Qn(x)≡0
Pn(x)-Qn(x)≡0  Пример Рунге Рассмотрим функцию f(x)=
Пример Рунге Рассмотрим функцию f(x)=  .
. т.е. является аналитической функцией.
т.е. является аналитической функцией. .
. (3)
(3)
 - многочлены n-ой степени,
- многочлены n-ой степени,  .
.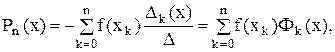 где
где  .
. - многочлен n-ой степени
- многочлен n-ой степени


 .
.
 , т.е. интерполяционный полином имеет вид:
, т.е. интерполяционный полином имеет вид: - интерполяционный полином Лагранжа
- интерполяционный полином Лагранжа а
а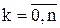 . (4)
. (4)
 .
. и обращается в ноль в (n+2) точках: x0…xn,x’.
и обращается в ноль в (n+2) точках: x0…xn,x’. обращается в ноль в по крайней мере (n+1) точке. И т.д.
обращается в ноль в по крайней мере (n+1) точке. И т.д. имеет хотя бы один нуль. Т.е.
имеет хотя бы один нуль. Т.е. 
 .
.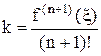 , а значит
, а значит  , т.к. точка x’ была выбрана произвольно.
, т.к. точка x’ была выбрана произвольно.
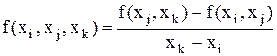


 ,
, 






 Кусочно-линейная функция, совпадающая в узлах с f(х) – линейный сплайн.
Кусочно-линейная функция, совпадающая в узлах с f(х) – линейный сплайн. порядка m для функции f(х) по разбиению Т – кусочно-полиномиальная функция, если:
порядка m для функции f(х) по разбиению Т – кусочно-полиномиальная функция, если: это многочлен m-ого порядка
это многочлен m-ого порядка
 .
. (m+1 коэффициент).
(m+1 коэффициент).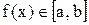 . В полиномиальной аппроксимации она приближается по значениям в узлах х0...хn линейной комбинацией степеней хk
. В полиномиальной аппроксимации она приближается по значениям в узлах х0...хn линейной комбинацией степеней хk 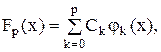 что их разность в некотором определенном смысле минимальна (в случае полиномиальной аппроксимации разность рассматривается в узлах).
что их разность в некотором определенном смысле минимальна (в случае полиномиальной аппроксимации разность рассматривается в узлах).

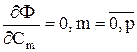





 - скалярное произведение φm на φk в L2 (а, b), то:
- скалярное произведение φm на φk в L2 (а, b), то: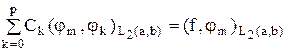
 линейно независима, следовательно, наилучшее средне квадратичное приближение существует и притом единственно.
линейно независима, следовательно, наилучшее средне квадратичное приближение существует и притом единственно. (натянутое на функции φ0...φр в пространстве L2 (а, b)).
(натянутое на функции φ0...φр в пространстве L2 (а, b)).
 - проекция f(х) на Вр+1. Приэтом она существует единственно, если φk линейно независима.
- проекция f(х) на Вр+1. Приэтом она существует единственно, если φk линейно независима.
 (1)
(1)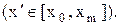

 Тогда при таком выборе К
Тогда при таком выборе К  и обращается в ноль в (n+2) точках (считая кратность): х0...хm, х'.
и обращается в ноль в (n+2) точках (считая кратность): х0...хm, х'.



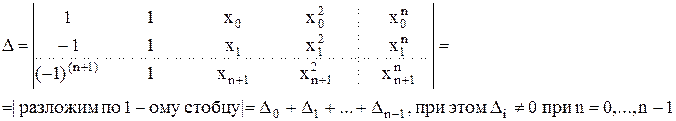 Заметим, что:
Заметим, что: - многочлен n-ого порядка с нулями
- многочлен n-ого порядка с нулями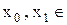 промежутку знакопостоянства функции.
промежутку знакопостоянства функции. - многочлен n-ого порядка с нулями
- многочлен n-ого порядка с нулями
 т.е. Pn(x,A)=Pn(x,A*).
т.е. Pn(x,A)=Pn(x,A*).
 .
.
 .
. и минимизирующий многочлен Pn(x,A0), если он существует.
и минимизирующий многочлен Pn(x,A0), если он существует. и минимизирующий многочлен Pn(x,Amin), если это возможно.
и минимизирующий многочлен Pn(x,Amin), если это возможно.
 - многочлен 1ой степени.
- многочлен 1ой степени.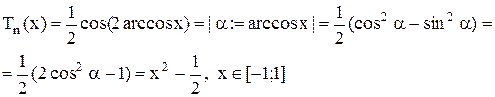
 . Докажем для n = k.
. Докажем для n = k. Заметим, что Tk-1(x) – многочлен степени k-1 по предположению, Tk-2(x) – многочлен степени (k-2). Таким образом, Tk(x) – многочлен степени k со старшим коэффициентом, равным 1.
Заметим, что Tk-1(x) – многочлен степени k-1 по предположению, Tk-2(x) – многочлен степени (k-2). Таким образом, Tk(x) – многочлен степени k со старшим коэффициентом, равным 1. - четная функция,
- четная функция, - нечетная.
- нечетная. .
. .
. .
. .
. - нули многочлена Чебышева Tn(x) на [-1;1].
- нули многочлена Чебышева Tn(x) на [-1;1]. При этом других нулей нет (т.к. многочлен nой степени имеет не более n нулей).
При этом других нулей нет (т.к. многочлен nой степени имеет не более n нулей). то точками экстремума для Тn(х) на [-1;1] будут точки, где
то точками экстремума для Тn(х) на [-1;1] будут точки, где 

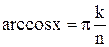
 где
где 
 .
.
 - экстреальные точки для Tn(x) на [-1;1].
- экстреальные точки для Tn(x) на [-1;1].
 (ортогональность в смысле Гильбертова пространства L2 [a;b]).
(ортогональность в смысле Гильбертова пространства L2 [a;b]).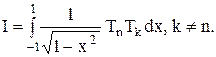


 .
. 2)
2)  , т.к. из предположения.
, т.к. из предположения.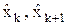 многочлен Qn(x) меняет свой знак. Т.е. многочлен Qn(x), отличный от нуля (т.к. он ≠0 в точках
многочлен Qn(x) меняет свой знак. Т.е. многочлен Qn(x), отличный от нуля (т.к. он ≠0 в точках  ) имеет n нулей, а значит Qn(x)≡0.
) имеет n нулей, а значит Qn(x)≡0. Пусть значения функции известны с малой точностью ε. Ответим на вопрос: останется ли в решении исходной задачи хотьо один достоверный знак. Рассмотрим приближенное равенство:
Пусть значения функции известны с малой точностью ε. Ответим на вопрос: останется ли в решении исходной задачи хотьо один достоверный знак. Рассмотрим приближенное равенство:  . При этом для достаточно гладких функций
. При этом для достаточно гладких функций  (погрешность первого порядка).
(погрешность первого порядка). . Она неограниченно возрастает при h→0.
. Она неограниченно возрастает при h→0.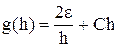 . А значит, оптимальным будет шаг метода, соответствующий минимуму g(h).
. А значит, оптимальным будет шаг метода, соответствующий минимуму g(h).
 . Т.е.
. Т.е. 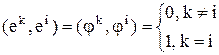 .
.

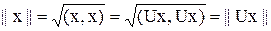 .
.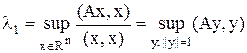 .
.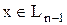 , то
, то  ).
).
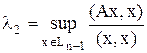 . Тогда из Леммы 2:
. Тогда из Леммы 2: .
. , повторим указанные в шаге два рассуждения.
, повторим указанные в шаге два рассуждения.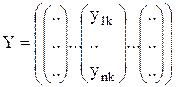 .
. Y.
Y. .
. . Докажем, что L=ker A.
. Докажем, что L=ker A.
 Т.е.
Т.е.  .
.
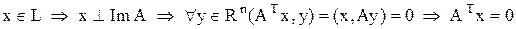
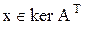 .
.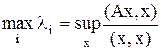 , то задача сводится к нахождению стационарных точек функционала
, то задача сводится к нахождению стационарных точек функционала  .
. .
. . Преобразуем правую часть равенства:
. Преобразуем правую часть равенства: при m>>1,
при m>>1,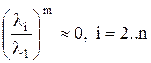 .
. ,
, - соответствующий собственный вектор
- соответствующий собственный вектор - знак находится по первой компоненте.
- знак находится по первой компоненте. .
. ;
; 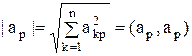 .
.


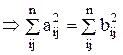
 отличается от В р-ой и q-ой строками:
отличается от В р-ой и q-ой строками: