
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Полиномиальная апппроксимацияСодержание книги Поиск на нашем сайте
Постановка задачи Из теорем математического анализа известно, что всякая непрерывная на отрезке [a;b] функция f(x) может быть хорошо приближена полиномом Pn(x). Теорема Вейерштрасса: Однако эта теорема не дает ответа на вопрос о существовании хорошего интерполяционного полинома для заданного множества точек {(xi, yi)}.
Пусть функция f(x) известна только в узлах некоторой сетки xi, т.е. задана таблицей: (xk≤xk+1)
Задача нахождения значений функции: a) между узлами ( б) вне узлов ( Теорема: Для всякой дискретной функции f(x), заданной предыдущей таблицей существует многочлен Pn(x) степени n, совпадающий в узлах с этой функцией (Pn(xk)=yk Доказательство Будем искать этот полином в виде: Pn(x)=a0+a1x+..+anxn. Запишем условие (1) в виде системы:
Будем считать, что все узлы – разные, т.е xk< xk+1. В данной системе неизвестные – ak. Определитель системы – отличный от нуля определитель Вандермонда:
Т.о. решение системы (2) существует, а значит существует многочлен Pn(x). Докажем его единственность. Предположим противное: существует Qn(x):
Определение Полином Pn(x) – интеполяционный полином для функции f(x).
Рассмотрим на [-1;1] ее интерполяционный многочлен (для значений по равномерным узлам): Pn(xk)= C возрастанием n многочлен также возрастает, увеличивая аксиляции колебаний.
Интерполяционный полином в форме Лагранжа Из системы (2) получим систему следующего вида:
Будем считать неизвестными a0,a1..an, -1. Полученная система имеет (n+1) порядок. Ее нетривиальное решение из предыдущей теоремы существует, следовательно, ее определитель равен 0 (иначе решение (3) было бы нулевым). Разложим этот определитель по последнему столбцу:
где
Перпишем последнее равенство в виде:
Заметим, что: 1) 2) 3) Следовательно, многочлен
Рассмотрим следующий многочлен (n+1)ой степени: Обозначим Заметим, что:
Т.о.
Погрешность интерполяции Представим функцию f(x) в виде: f(x)=Pn(x)+Rn(x), где Rn(x) – погрешность интерполяции. Заметим, что Rn(x) зависит от свойств f(x) (так если f(x) линейна, то Rn(x)≡0 при n>2). Будем считать априорно, что Запишем погрешность в виде: Rn(x)=kωn+1(x)+φ(x). Тогда φ(x)=f(x)-Pn(x)- kωn+1(x) и φ(xk)=0, Выберем k из условия φ(x’)=0, где x’ – точка, в которой оценивается погрешность: Из уравнения φ(x’)=0 получим: При таком выборе k φ(x’) Тогда по т. Ролля По т. Ролля Т.о. из (4) получим:
Тогда
Интерполяционный полином в форме Ньютона Рассматривается функция f(х), заданная дискретно в узлах х0...хn. Ставится задача её аппроксимации по этим данным. Введём понятие разделённых разностей: 1-ого порядка - 2-ого порядка - k-ого порядка - нулевого порядка -
Тогда:
....................
....................
Из первого равенства получим:
Обозначим все слагаемые, кроме последнего как Рn(х), последнее - Rn(х). Рn(х) – интерполяционный полином (т.к. он порядка n и совпадает в узлах с f(х)) Ньютона.
Следствие: Аппроксимация сплайнами Рассматривается задача приближения функции f(х) на некотором интервале по её значениям в узлах х0...хn (хk< хk+1
Обозначим разбиение {x0…xn} как Т.
Сплайн 1) на каждом из отрезков [xk-1, xk] 2) в узлах совпадает с функцией f(х): 3) во внутренних узлах (х1...хn-1) эта функция непрерывна вместе со своими производными до (m-1)-ого порядка
Построение сплайна Обозначим многочлен, который необходимо найти на [xk-1, xk] как:
Из условия 2) для сплайна => (n+1) уравнение. Из условия 3) => (n-1) уравнение для каждой из m функций. Итого всего уравнений для сплайна: n+1+m(n-1)=n(m+1)+1-m Всего неизвестных коэффициентов (m+1) для каждого из n отрезков, т.е. n(m+1). Таким образом, число уравнений и искомых коэффициентов совпадает при m=1, иначе условий не хватает для нахождения коэффициентов, и требуются дополнительные условия.
Основные сплайны: - 1-ого порядка – линейные; - 2-ого порядка – кубические (m=3). Для них 4n-2 уравнения и 4n коэффициентов. В качестве двух дополнительных условий обычно задают значения производных в двух узлах. Таким образом, функция f(х) может быть интерполирована на [x0, xn] сплайном заданного порядка.
Метод наименьших квадратов Рассмотрим некоторую функцию Таким образом, функцию f(х) на [a,b], заданную в узлах х0...хn можно аппроксимировать некоторыми функциями φk(k), общее число которых (р+1), р≠n. Рассмотрим некоторые употребляемые частные случаи: 1) Полиномиальная задача: найти для функции f(х) такую линейную комбинацию функций φk: Рассмотрим следующее выражение:
Необходимое условие минимума функции
Таким образом, получим следующую систему уравнений:
Или:
2) Континуальная задача: аппроксимировать функцию f(х) в С [a, b] в смысле средне квадратичного. Обозначим Необходимое условие экстремума имеет вид:
Получим систему:
Или:
т.к.
Определитель с матрицей А=(аkm), где аkm= (φk, φm) – определитель Грамма.
Заметим, что det А≠0, если система Рассмотрим подпространство
|
||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 572; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.87.145 (0.008 с.) |


 ) – задача интерполяции
) – задача интерполяции ) – задача экстраполяции
) – задача экстраполяции ) и он единственен. (1)
) и он единственен. (1) (2)
(2)
 . Тогда полином Pn(x)-Qn(x) равен 0 в (n+1) точке
. Тогда полином Pn(x)-Qn(x) равен 0 в (n+1) точке  Pn(x)-Qn(x)≡0
Pn(x)-Qn(x)≡0  Пример Рунге Рассмотрим функцию f(x)=
Пример Рунге Рассмотрим функцию f(x)=  .
. т.е. является аналитической функцией.
т.е. является аналитической функцией. .
. (3)
(3)
 - многочлены n-ой степени,
- многочлены n-ой степени,  .
.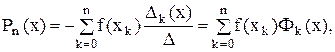 где
где  .
. - многочлен n-ой степени
- многочлен n-ой степени


 .
.
 , т.е. интерполяционный полином имеет вид:
, т.е. интерполяционный полином имеет вид: - интерполяционный полином Лагранжа
- интерполяционный полином Лагранжа а
а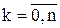 . (4)
. (4)
 .
. и обращается в ноль в (n+2) точках: x0…xn,x’.
и обращается в ноль в (n+2) точках: x0…xn,x’. обращается в ноль в по крайней мере (n+1) точке. И т.д.
обращается в ноль в по крайней мере (n+1) точке. И т.д. имеет хотя бы один нуль. Т.е.
имеет хотя бы один нуль. Т.е. 
 .
.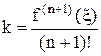 , а значит
, а значит  , т.к. точка x’ была выбрана произвольно.
, т.к. точка x’ была выбрана произвольно.
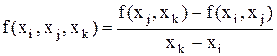


 ,
, 






 Кусочно-линейная функция, совпадающая в узлах с f(х) – линейный сплайн.
Кусочно-линейная функция, совпадающая в узлах с f(х) – линейный сплайн. порядка m для функции f(х) по разбиению Т – кусочно-полиномиальная функция, если:
порядка m для функции f(х) по разбиению Т – кусочно-полиномиальная функция, если: это многочлен m-ого порядка
это многочлен m-ого порядка
 .
. (m+1 коэффициент).
(m+1 коэффициент).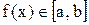 . В полиномиальной аппроксимации она приближается по значениям в узлах х0...хn линейной комбинацией степеней хk
. В полиномиальной аппроксимации она приближается по значениям в узлах х0...хn линейной комбинацией степеней хk 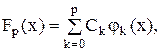 что их разность в некотором определенном смысле минимальна (в случае полиномиальной аппроксимации разность рассматривается в узлах).
что их разность в некотором определенном смысле минимальна (в случае полиномиальной аппроксимации разность рассматривается в узлах).

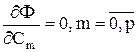





 - скалярное произведение φm на φk в L2 (а, b), то:
- скалярное произведение φm на φk в L2 (а, b), то: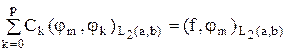
 линейно независима, следовательно, наилучшее средне квадратичное приближение существует и притом единственно.
линейно независима, следовательно, наилучшее средне квадратичное приближение существует и притом единственно. (натянутое на функции φ0...φр в пространстве L2 (а, b)).
(натянутое на функции φ0...φр в пространстве L2 (а, b)).
 - проекция f(х) на Вр+1. Приэтом она существует единственно, если φk линейно независима.
- проекция f(х) на Вр+1. Приэтом она существует единственно, если φk линейно независима.


