Интерполяционные формулы для неравноотстоящих узлов
Похожие статьи вашей тематики
Пусть известны значения некоторой функции   в n +1 различных точках в n +1 различных точках  , которые обозначим следующим образом: , которые обозначим следующим образом: 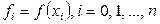 . .
Указанные значения могут быть получены путем экспериментальных измерений или найдены с помощью достаточно сложных вычислений. В задаче интерполяции  функции функции  , как было сказано ранее, решается проблема приближенного восстановления значения функции в произвольной точке x. Для этого строится алгебраический многочлен , как было сказано ранее, решается проблема приближенного восстановления значения функции в произвольной точке x. Для этого строится алгебраический многочлен  степени n, который в точках степени n, который в точках 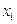 принимает заданные значения, т. е. принимает заданные значения, т. е.
 . (1.4) . (1.4)
Следует заметить, что если точка x расположена вне минимального отрезка, содержащего все узлы интерполяции  , то замену функции , то замену функции  на на  также называют экстраполяцией. также называют экстраполяцией.
В общем случае доказано, что существует единственный интерполяционный многочлен n -й степени, удовлетворяющий условиям (1.4),
 , (1.5) , (1.5)
где
 . (1.6) . (1.6)
Интерполяционный многочлен, представленный в виде (1.5), называется интерполяционным многочленом Лагранжа, а функции (1.6) - лагранжевыми коэффициентами [1]-[4].
Для оценки погрешности интерполяции (в частности, и экстраполяции) в текущей точке  ( ( - отрезок, содержащий все узлы интерполяции - отрезок, содержащий все узлы интерполяции  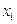 и точку x) можно использовать соотношение и точку x) можно использовать соотношение
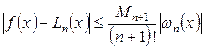 , (1.7) , (1.7)
где  ; ; 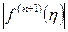 - (n +1)-я производная интерполируемой функции в некоторой точке - (n +1)-я производная интерполируемой функции в некоторой точке  ; ;  . .
Оценить максимальную погрешность интерполяции на всем отрезке  можно с помощью соотношения можно с помощью соотношения
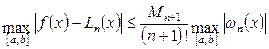 . (1.8) . (1.8)
Использование оценок погрешностей (1.7) и (1.8) предполагает ограниченность (n +1)-й производной интерполируемой функции на отрезке  , т. е. , т. е. 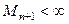 . .
На практике вместо общей формы записи (1.5) часто используются другие формы записи интерполяционного многочлена, более удобные для применения в конкретных ситуациях [5], [10], [12].
Интерполяционный многочлен Ньютона для неравноотстоящих узлов интерполяции имеет вид
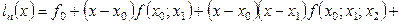 … …
… 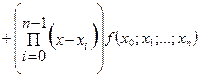 , (1.9) , (1.9)
где 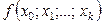 - разделенная разность k -го порядка. - разделенная разность k -го порядка.
Вычисление разделенных разностей производится по соотношениям
 , ,
...................................................
 . .
При использовании интерполяционного многочлена Ньютона (1.9) изменение степени n требует только добавить или отбросить соответствующее число стандартных слагаемых, что удобно на практике. В то же время, непосредственное использование интерполяционного многочлена Лагранжа (1.5) требует строить его заново при изменении n.
В том случае, если требуется найти лишь численное значение интерполяционного многочлена  , а не его представление, может быть использована итерационно-интерполяционная схема Эйткена [6], [12]. , а не его представление, может быть использована итерационно-интерполяционная схема Эйткена [6], [12].
Пусть  - интерполяционный многочлен, определяемый парами - интерполяционный многочлен, определяемый парами 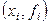 , , 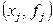 , , 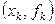 ,... так, что ,... так, что 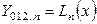 . .
Интерполяционные многочлены возрастающих степеней получают последовательно следующим образом:
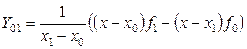 , ,
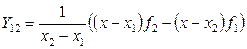 , ,
...…..............................................
 , ,
......................................................
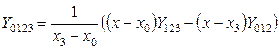 . .
......................................................
Этот процесс можно закончить, когда у значений двух интерполяционных многочленов последовательных степеней совпадает требуемое количество знаков.
Лабораторная работа № 9*
В ходе работы студенты должны самостоятельно разработать программу на одном из языков программирования, обеспечивающую решение одного из вариантов, полученного от преподавателя. Варианты задания приводятся ниже.
Вариант 1
x = 2.7704
| X[ 0] = 0.7728
| Y[ 0] = -0.6210
| | X[ 1] = 0.7912
| Y[ 1] = -0.5575
| | X[ 2] = 1.4488
| Y[ 2] = 0.3837
| | X[ 3] = 2.2336
| Y[ 3] = -0.2209
| | X[ 4] = 3.2776
| Y[ 4] = 0.8078
| | X[ 5] = 4.8128
| Y[ 5] = 19.4416
| | X[ 6] = 4.8312
| Y[ 6] = 19.8628
| | X[ 7] = 5.1360
| Y[ 7] = 27.7050
| | X[ 8] = 5.2128
| Y[ 8] = 29.9500
| | X[ 9] = 6.3272
| Y[ 9] = 76.6981
| | X[10] = 6.3520
| Y[10] = 78.0745
| | Используя интерполяционную схему Эйткена либо интерполяционную формулу Ньютона, вычислите значение в точке x функции, заданной таблицей.
Вариант 2
x = 2.3904
| X[ 0] = 0.0376
| Y[ 0] = -5.5948
| | X[ 1] = 0.4208
| Y[ 1] = -2.3591
| | X[ 2] = 0.6800
| Y[ 2] = -0.9800
| | X[ 3] = 1.5360
| Y[ 3] = 0.3641
| | X[ 4] = 2.7056
| Y[ 4] = -0.3543
| | X[ 5] = 3.6888
| Y[ 5] = 3.1277
| | X[ 6] = 3.8448
| Y[ 6] = 4.4336
| | X[ 7] = 4.2944
| Y[ 7] = 9.7839
| | X[ 8] = 4.4048
| Y[ 8] = 11.5023
| | X[ 9] = 5.4200
| Y[ 9] = 36.5817
| | X[10] = 5.8192
| Y[10] = 51.8888
| |
Вариант 4
x = 2.3664
| X[ 0] = 1.9816
| Y[ 0 ]= 0.0184
| | X[ 1] = 2.0952
| Y[ 1] = -0.0943
| | X[ 2] = 2.1016
| Y[ 2] = -0.1006
| | X[ 3] = 2.7384
| Y[ 3] = -0.3358
| | X[ 4] = 2.8872
| Y[ 4] = -0.1889
| | X[ 5] = 3.4816
| Y[ 5] = 1.7707
| | X[ 6] = 4.0768
| Y[ 6] = 6.8806
| | X[ 7] = 4.9888
| Y[ 7] = 23.7099
| | X[ 8] = 5.1256
| Y[ 8] = 27.4096
| | X[ 9] = 5.5200
| Y[ 9] = 40.0942
| | X[10] = 5.6544
| Y[10] = 45.1488
| |
Вариант 3
x = 4.8392
| X[ 0] = 0.3152
| Y[ 0] = -3.0976
| | X[ 1] = 0.9536
| Y[ 1] = -0.0994
| | X[ 2] = 1.1080
| Y[ 2] = 0.1823
| | X[ 3] = 2.4728
| Y[ 3] = -0.3671
| | X[ 4] = 4.1792
| Y[ 4] = 8.1696
| | X[ 5] = 4.5616
| Y[ 5] = 14.2471
| | X[ 6] = 4.6304
| Y[ 6] = 15.5694
| | X[ 7] = 4.6704
| Y[ 7] = 16.3723
| | X[ 8] = 5.2480
| Y[ 8] = 31.0168
| | X[ 9] = 5.5680
| Y[ 9] = 41.8549
| | X[10] = 6.3568
| Y[10] = 78.3427
| |
Вариант 5
x = 4.9080
| X[ 0] = 0.4312
| Y[ 0] = -2.2922
| | X[ 1] = 0.6328
| Y[ 1] = -1.1884
| | X[ 2] = 1.2560
| Y[ 2] = 0.3322
| | X[ 3] = 2.1296
| Y[ 3] = -0.1274
| | X[ 4] = 2.1928
| Y[ 4] = -0.1856
| | X[ 5] = 2.8848
| Y[ 5] = -0.1921
| | X[ 6] = 4.2808
| Y[ 6] = 9.5840
| | X[ 7] = 4.7896
| Y[ 7] = 18.9187
| | X[ 8] = 4.8264
| Y[ 8] = 19.7524
| | X[ 9] = 5.3368
| Y[ 9] = 33.8159
| | X[10] = 5.9344
| Y[10] = 56.9682
| Вариант 6
x = 1.2952
| X[ 0] = 0.2744
| Y[ 0] = -3.4127
| | X[ 1] = 0.3096
| Y[ 1] = -3.1398
| | X[ 2] = 0.4736
| Y[ 2] = -2.0300
| | X[ 3] = 1.8048
| Y[ 3] = 0.1878
| | X[ 4] = 2.4888
| Y[ 4] = -0.3720
| | X[ 5] = 2.9832
| Y[ 5] = -0.0328
| | X[ 6] = 3.4832
| Y[ 6] = 1.7797
| | X[ 7] = 4.1840
| Y[ 7] = 8.2334
| | X[ 8] = 4.2944
| Y[ 8] = 9.7839
| | X[ 9] = 5.5352
| Y[ 9] = 40.6465
| | X[10] = 5.7016
| Y[10] = 47.0171
| Вариант 7
x = 4.7296
| X[ 0] = 0.5016
| Y[ 0] = -1.8658
| | X[ 1] = 1.2472
| Y[ 1] = 0.3262
| | X[ 2] = 2.4400
| Y[ 2] = -0.3548
| | X[ 3] = 2.5432
| Y[ 3] = -0.3829
| | X[ 4] = 2.9296
| Y[ 4] = -0.1263
| | X[ 5] = 2.9584
| Y[ 5] = -0.0781
| | X[ 6] = 3.2336
| Y[ 6] = 0.6437
| | X[ 7] = 3.2944
| Y[ 7] = 0.8743
| | X[ 8] = 3.9368
| Y[ 8] = 5.3285
| | X[ 9] = 5.7816
| Y[ 9] = 50.2972
| | X[10] = 6.0488
| Y[10] = 62.3223
| Вариант 8
x = 3.7488
| X[ 0] = 0.2912
| Y[ 0] = -3.2809
| | X[ 1] = 0.4408
| Y[ 1] = -2.2314
| | X[ 2] = 1.4016
| Y[ 2] = 0.3841
| | X[ 3] = 1.8952
| Y[ 3] = 0.1036
| | X[ 4] = 2.3360
| Y[ 4] = -0.2981
| | X[ 5] = 2.9272
| Y[ 5] = -0.1301
| | X[ 6] = 4.4032
| Y[ 6] = 11.4762
| | X[ 7] = 5.4240
| Y[ 7] = 36.7182
| | X[ 8] = 5.6920
| Y[ 8] = 46.6331
| | X[ 9] = 6.0904
| Y[ 9] = 64.3476
| | X[10] = 6.5176
| Y[10] = 87.6808
| |
Вариант 12
x = 5.4008
| X[ 0] = 0.7416
| Y[ 0] = -0.7344
| | X[ 1] = 0.9752
| Y[ 1] = -0.0515
| | X[ 2] = 1.1664
| Y[ 2] = 0.2543
| | X[ 3] = 1.5400
| Y[ 3] = 0.3627
| | X[ 4] = 3.7888
| Y[ 4] = 3.9350
| | X[ 5] = 3.8776
| Y[ 5] = 4.7417
| | X[ 6] = 4.5128
| Y[ 6] = 13.3534
| | X[ 7] = 4.9328
| Y[ 7] = 22.2931
| | X[ 8] = 5.1840
| Y[ 8] = 29.0949
| | X[ 9] = 5.5352
| Y[ 9] = 40.6465
| | X[10] = 5.6976
| Y[10] = 46.8569
| Вариант 11
x = 4.2696
| X[ 0] = 0.3264
| Y[ 0] = -3.0140
| | X[ 1] = 1.4240
| Y[ 1] = 0.3849
| | X[ 2] = 2.4760
| Y[ 2] = -0.3681
| | X[ 3] = 4.4048
| Y[ 3] = 11.5023
| | X[ 4] = 4.4952
| Y[ 4] = 13.0400
| | X[ 5] = 5.4320
| Y[ 5] = 36.9922
| | X[ 6] = 5.6088
| Y[ 6] = 43.3902
| | X[ 7] = 5.9272
| Y[ 7] = 56.6416
| | X[ 8] = 6.0936
| Y[ 8] = 64.5051
| | X[ 9] = 6.3560
| Y[ 9] = 78.2980
| | X[10] = 6.3720
| Y[10] = 79.1961
| | Вариант 14
x = 3.5896
| X[ 0] = 0.3384
| Y[ 0] = -2.9259
| | X[ 1] = 0.8184
| Y[ 1] = -0.4681
| | X[ 2] = 2.0424
| Y[ 2] = -0.0423
| | X[ 3] = 2.2264
| Y[ 3] = -0.2148
| | X[ 4] = 2.9240
| Y[ 4] = -0.1351
| | X[ 5] = 3.8272
| Y[ 5] = 4.2732
| | X[ 6] = 4.6800
| Y[ 6] = 16.5688
| | X[ 7] = 5.1360
| Y[ 7] = 27.7050
| | X[ 8] = 5.3272
| Y[ 8] = 33.5058
| | X[ 9] = 6.1688
| Y[ 9] = 68.2803
| | X[10] = 6.1744
| Y[10] = 68.5671
| Вариант 13
x = 4.6504
| X[ 0] = 0.1984
| Y[ 0] = -4.0460
| | X[ 1] = 1.3648
| Y[ 1] = 0.3789
| | X[ 2] = 2.0112
| Y[ 2] = -0.0112
| | X[ 3] = 2.2728
| Y[ 3] = -0.2525
| | X[ 4] = 2.2824
| Y[ 4] = -0.2599
| | X[ 5] = 2.5472
| Y[ 5] = -0.3834
| | X[ 6] = 3.6512
| Y[ 6] = 2.8507
| | X[ 7] = 4.0120
| Y[ 7] = 6.1329
| | X[ 8] = 5.0336
| Y[ 8] = 24.8838
| | X[ 9] = 5.1064
| Y[ 9] = 26.8695
| | X[10] = 5.6600
| Y[10] = 45.3679
| | Вариант 16
x = 3.9336
| X[ 0] = 0.0840
| Y[ 0] = -5.1177
| | X[ 1] = 0.1976
| Y[ 1] = -4.0530
| | X[ 2] = 0.2304
| Y[ 2] = -3.7719
| | X[ 3] = 1.3144
| Y[ 3] = 0.3633
| | X[ 4] = 1.6712
| Y[ 4] = 0.2933
| | X[ 5] = 1.9336
| Y[ 5] = 0.0661
| | X[ 6] = 2.0808
| Y[ 6] = -0.0803
| | X[ 7] = 2.2256
| Y[ 7] = -0.2141
| | X[ 8] = 2.5096
| Y[ 8] = -0.3773
| | X[ 9] = 6.2688
| Y[ 9] = 73.5201
| | X[10] = 6.5072
| Y[10] = 87.0559
| Вариант 15
x = 2.2248
| X[ 0] = 0.2376
| Y[ 0] = -3.7117
| | X[ 1] = 0.7368
| Y[ 1] = -0.7525
| | X[ 2] = 1.1448
| Y[ 2] = 0.2297
| | X[ 3] = 1.9872
| Y[ 3] = 0.0128
| | X[ 4] = 2.5392
| Y[ 4] = -0.3824
| | X[ 5] = 2.7648
| Y[ 5] = -0.3175
| | X[ 6] = 3.0616
| Y[ 6] = 0.1348
| | X[ 7] = 3.2088
| Y[ 7] = 0.5575
| | X[ 8] = 3.2784
| Y[ 8] = 0.8109
| | X[ 9] = 3.6904
| Y[ 9] = 3.1398
| | X[10] = 3.9368
| Y[10] = 5.3285
| | Вариант 18
x = 4.1840
| X[ 0] = 1.2304
| Y[ 0] = 0.3138
| | X[ 1] = 2.7344
| Y[ 1] = -0.3383
| | X[ 2] = 2.9920
| Y[ 2] = -0.0158
| | X[ 3] = 4.1320
| Y[ 3] = 7.5588
| | X[ 4] = 4.5472
| Y[ 4] = 13.9796
| | X[ 5] = 4.8232
| Y[ 5] = 19.6790
| | X[ 6] = 4.9440
| Y[ 6] = 22.5720
| | X[ 7] = 5.3408
| Y[ 7] = 33.9457
| | X[ 8] = 5.8088
| Y[ 8] = 51.4453
| | X[ 9] = 6.0424
| Y[ 9] = 62.0144
| | X[10] = 6.0800
| Y[10] = 63.8373
| Вариант 17
x = 4.8592
| X[ 0] = 0.0280
| Y[ 0] = -5.6967
| | X[ 1] = 1.5512
| Y[ 1] = 0.3584
| | X[ 2] = 1.6088
| Y[ 2] = 0.3313
| | X[ 3] = 2.3360
| Y[ 3] = -0.2981
| | X[ 4] = 2.5600
| Y[ 4] = -0.3844
| | X[ 5] = 2.8920
| Y[ 5] = -0.1823
| | X[ 6] = 2.9352
| Y[ 6] = -0.1173
| | X[ 7] = 5.3416
| Y[ 7] = 33.9717
| | X[ 8] = 5.8320
| Y[ 8] = 52.4379
| | X[ 9] = 6.4424
| Y[ 9] = 83.2280
| | X[10] = 6.5120
| Y[10] = 87.3439
| | Вариант 20
x = 3.7416
| X[ 0] = 0.5512
| Y[ 0] = -1.5923
| | X[ 1] = 1.9104
| Y[ 1] = 0.0889
| | X[ 2] = 2.5024
| Y[ 2] = -0.3756
| | X[ 3] = 2.6328
| Y[ 3] = -0.3794
| | X[ 4] = 3.2656
| Y[ 4] = 0.7616
| | X[ 5] = 3.3544
| Y[ 5] = 1.1301
| | X[ 6] = 3.7880
| Y[ 6] = 3.9281
| | X[ 7] = 4.0008
| Y[ 7] = 6.0088
| | X[ 8] = 4.3832
| Y[ 8] = 11.1525
| | X[ 9] = 4.4704
| Y[ 9] = 12.6061
| | X[10] = 5.6872
| Y[10] = 46.4419
| | Вариант 19
x = 4.0416
| X[ 0] = 0.4184
| Y[ 0] = -2.3747
| | X[ 1] = 0.7288
| Y[ 1] = -0.7830
| | X[ 2] = 1.0008
| Y[ 2] = 0.0016
| | X[ 3] = 1.6520
| Y[ 3] = 0.3059
| | X[ 4] = 3.2800
| Y[ 4] = 0.8172
| | X[ 5] = 3.8888
| Y[ 5] = 4.8496
| | X[ 6] = 4.7568
| Y[ 6] = 18.1947
| | X[ 7] = 5.1384
| Y[ 7] = 27.7734
| | X[ 8] = 5.3536
| Y[ 8] = 34.3631
| | X[ 9] = 5.8096
| Y[ 9] = 51.4793
| | X[10] = 6.3464
| Y[10] = 77.7623
| Вариант 22
x = 1.1744
| X[ 0] = 0.6320
| Y[ 0] = -1.1921
| | X[ 1] = 0.9856
| Y[ 1] = -0.0294
| | X[ 2] = 1.1616
| Y[ 2] = 0.2491
| | X[ 3] = 1.9552
| Y[ 3] = 0.0447
| | X[ 4] = 3.1432
| Y[ 4] = 0.3509
| | X[ 5] = 4.0440
| Y[ 5] = 6.4957
| | X[ 6] = 4.0992
| Y[ 6] = 7.1512
| | X[ 7] = 5.0920
| Y[ 7] = 26.4690
| | X[ 8] = 5.9144
| Y[ 8] = 56.0641
| | X[ 9] = 6.0944
| Y[ 9] = 64.5446
| | X[10] = 6.4024
| Y[10] = 80.9211
| | Вариант 21
x = 2.5512
| X[ 0] = 0.3440
| Y[ 0] = -2.8853
| | X[ 1] = 0.3680
| Y[ 1] = -2.7147
| | X[ 2] = 0.7016
| Y[ 2] = -0.8905
| | X[ 3] = 1.2896
| Y[ 3] = 0.3519
| | X[ 4] = 2.8680
| Y[ 4] = -0.2140
| | X[ 5] = 2.8968
| Y[ 5] = -0.1755
| | X[ 6] = 4.2560
| Y[ 6] = 9.2260
| | X[ 7] = 4.4344
| Y[ 7] = 11.9926
| | X[ 8] = 4.9264
| Y[ 8] = 22.1348
| | X[ 9] = 5.3416
| Y[ 9] = 33.9717
| | X[10] = 6.3888
| Y[10] = 80.1464
| |
Вариант 24
x = 2.7176
| X[ 0] = 0.0328
| Y[ 0] = -5.6456
| | X[ 1] = 0.4440
| Y[ 1] = -2.2113
| | X[ 2] = 0.9784
| Y[ 2] = -0.0446
| | X[ 3] = 1.6776
| Y[ 3] = 0.2889
| | X[ 4] = 4.1312
| Y[ 4] = 7.5487
| | X[ 5] = 4.7896
| Y[ 5] = 18.9187
| | X[ 6] = 4.8144
| Y[ 6] = 19.4780
| | X[ 7] = 5.4640
| Y[ 7] = 38.1016
| | X[ 8] = 5.5928
| Y[ 8] = 42.7838
| | X[ 9] = 6.3488
| Y[ 9] = 77.8960
| | X[10] = 6.3584
| Y[10] = 78.4322
| Вариант 23
x = 3.0120
| X[ 0] = 0.4032
| Y[ 0] = -2.4747
| | X[ 1] = 0.9736
| Y[ 1] = -0.0549
| | X[ 2] = 2.2856
| Y[ 2] = -0.2623
| | X[ 3] = 3.6472
| Y[ 3] = 2.8221
| | X[ 4] = 3.6528
| Y[ 4] = 2.8622
| | X[ 5] = 4.5176
| Y[ 5] = 13.4397
| | X[ 6] = 4.9120
| Y[ 6] = 21.7810
| | X[ 7] = 5.6952
| Y[ 7] = 46.7609
| | X[ 8] = 5.8736
| Y[ 8] = 54.2489
| | X[ 9] = 5.8776
| Y[ 9] = 54.4252
| | X[10] = 6.0640
| Y[10] = 63.0574
| | Вариант 26
x = 1.7208
| X[ 0] = 0.2448
| Y[ 0] = -3.6521
| | X[ 1] = 0.7272
| Y[ 1] = -0.7892
| | X[ 2] = 1.0544
| Y[ 2] = 0.1001
| | X[ 3] = 1.0728
| Y[ 3] = 0.1301
| | X[ 4] = 1.8864
| Y[ 4] = 0.1121
| | X[ 5] = 2.3712
| Y[ 5] = -0.3201
| | X[ 6] = 5.0128
| Y[ 6] = 24.3343
| | X[ 7] = 5.1624
| Y[ 7] = 28.4640
| | X[ 8] = 5.4768
| Y[ 8] = 38.5512
| | X[ 9] = 5.6240
| Y[ 9] = 43.9714
| | X[10] = 6.3288
| Y[10] = 76.7865
| Вариант 25
x = 2.4800
| X[ 0] = 0.8496
| Y[ 0] = -0.3721
| | X[ 1] = 0.9648
| Y[ 1] = -0.0742
| | X[ 2] = 1.4072
| Y[ 2] = 0.3845
| | X[ 3] = 1.8048
| Y[ 3] = 0.1878
| | X[ 4] = 2.1920
| Y[ 4] = -0.1849
| | X[ 5] = 2.4232
| Y[ 5] = -0.3474
| | X[ 6] = 3.6152
| Y[ 6] = 2.5986
| | X[ 7] = 3.6800
| Y[ 7] = 3.0616
| | X[ 8] = 4.5024
| Y[ 8] = 13.1676
| | X[ 9] = 5.1672
| Y[ 9] = 28.6035
| | X[10] = 6.0424
| Y[10] = 62.0144
| | Вариант 28
x = 0.9512
| X[ 0] = 0.0760
| Y[ 0] = -5.1982
| | X[ 1] = 2.0776
| Y[ 1] = -0.0771
| | X[ 2] = 2.0840
| Y[ 2] = -0.0834
| | X[ 3] = 2.5120
| Y[ 3] = -0.3778
| | X[ 4] = 2.9368
| Y[ 4] = -0.1147
| | X[ 5] = 4.0872
| Y[ 5] = 7.0055
| | X[ 6] = 4.7168
| Y[ 6] = 17.3359
| | X[ 7] = 5.0096
| Y[ 7] = 24.2504
| | X[ 8] = 5.0720
| Y[ 8] = 25.9190
| | X[ 9] = 5.1176
| Y[ 9] = 27.1837
| | X[10] = 6.3472
| Y[10] = 77.8068
| Вариант 27
x = 2.6816
| X[ 0] = 0.1096
| Y[ 0] = -4.8652
| | X[ 1] = 1.1240
| Y[ 1] = 0.2038
| | X[ 2] = 1.3096
| Y[ 2] = 0.3613
| | X[ 3] = 2.0608
| Y[ 3] = -0.0606
| | X[ 4] = 2.4160
| Y[ 4] = -0.3440
| | X[ 5] = 3.6336
| Y[ 5] = 2.7259
| | X[ 6] = 4.6504
| Y[ 6] = 15.9677
| | X[ 7] = 5.0360
| Y[ 7] = 24.9477
| | X[ 8] = 5.3056
| Y[ 8] = 32.8147
| | X[ 9] = 5.5000
| Y[ 9] = 39.3750
| | X[10] = 5.8064
| Y[10] = 51.3433
| |
Вариант 30
x = 0.5040
| X[ 0] = 0.0288
| Y[ 0] = -5.6882
| | X[ 1] = 1.3400
| Y[ 1] = 0.3725
| | X[ 2] = 1.4400
| Y[ 2] = 0.3844
| | X[ 3] = 1.4432
| Y[ 3] = 0.3842
| | X[ 4] = 1.8200
| Y[ 4] = 0.1742
| | X[ 5] = 2.0736
| Y[ 5] = -0.0732
| | X[ 6] = 2.2944
| Y[ 6] = -0.2689
| | X[ 7] = 3.3984
| Y[ 7] = 1.3362
| | X[ 8] = 5.7960
| Y[ 8] = 50.9029
| | X[ 9] = 5.7984
| Y[ 9] = 51.0043
| | X[10] = 6.2160
| Y[10] = 70.7220
| Вариант 29
x = 2.4712
| X[ 0] = 0.6984
| Y[ 0] = -0.9035
| | X[ 1] = 0.7232
| Y[ 1] = -0.8047
| | X[ 2] = 0.7720
| Y[ 2] = -0.6238
| | X[ 3] = 0.8320
| Y[ 3] = -0.4254
| | X[ 4] = 2.0720
| Y[ 4] = -0.0716
| | X[ 5] = 3.6336
| Y[ 5] = 2.7259
| | X[ 6] = 3.6352
| Y[ 6] = 2.7371
| | X[ 7] = 4.7624
| Y[ 7] = 18.3171
| | X[ 8] = 4.8496
| Y[ 8] = 20.2898
| | X[ 9] = 5.3008
| Y[ 9] = 32.6623
| | X[10] = 6.4264
| Y[10] = 82.3001
| | Вариант 32
x = 5.5232
| X[ 0] = 0.1008
| Y[ 0] = -4.9511
| | X[ 1] = 0.1328
| Y[ 1] = -4.6427
| | X[ 2] = 0.1648
| Y[ 2] = -4.3457
| | X[ 3] = 1.3200
| Y[ 3] = 0.3656
| | X[ 4] = 1.8400
| Y[ 4] = 0.1559
| | X[ 5] = 2.2912
| Y[ 5] = -0.2665
| | X[ 6] = 3.7360
| Y[ 6] = 3.4958
| | X[ 7] = 3.9376
| Y[ 7] = 5.3367
| | X[ 8] = 5.7680
| Y[ 8] = 49.7294
| | X[ 9] = 5.9912
| Y[ 9] = 59.5873
| | X[10] = 6.4976
| Y[10] = 86.4817
| | Вариант 31
x = 4.5296
| X[ 0] = 0.2816
| Y[ 0] = -3.3559
| | X[ 1] = 1.7768
| Y[ 1] = 0.2121
| | X[ 2] = 2.1120
| Y[ 2] = -0.1106
| | X[ 3] = 2.2696
| Y[ 3] = -0.2500
| | X[ 4] = 2.4360
| Y[ 4] = -0.3531
| | X[ 5] = 3.2456
| Y[ 5] = 0.6870
| | X[ 6] = 3.4176
| Y[ 6] = 1.4312
| | X[ 7] = 3.6312
| Y[ 7] = 2.7091
| | X[ 8] = 5.4512
| Y[ 8] = 37.6553
| | X[ 9] = 5.8664
| Y[ 9] = 53.9326
| | X[10] = 5.9432
| Y[10] = 57.3689
| | Вариант 34
x = 5.4408
| X[ 0] = 0.3000
| Y[ 0] = -3.2130
| | X[ 1] = 0.3544
| Y[ 1] = -2.8107
| | X[ 2] = 0.6360
| Y[ 2] = -1.1737
| | X[ 3] = 0.7328
| Y[ 3] = -0.7677
| | X[ 4] = 1.8096
| Y[ 4] = 0.1835
| | X[ 5] = 1.8280
| Y[ 5] = 0.1669
| | X[ 6] = 2.1040
| Y[ 6] = -0.1029
| | X[ 7] = 4.2888
| Y[ 7] = 9.7013
| | X[ 8] = 5.3952
| Y[ 8] = 35.7426
| | X[ 9] = 6.0464
| Y[ 9] = 62.2067
| | X[10] = 6.4096
| Y[10] = 81.3332
| | Вариант 33
x = 2.1976
| X[ 0] = 0.2712
| Y[ 0] = -3.4381
| | X[ 1] = 0.4336
| Y[ 1] = -2.2769
| | X[ 2] = 0.4648
| Y[ 2] = -2.0830
| | X[ 3] = 0.6368
| Y[ 3] = -1.1701
| | X[ 4] = 1.8176
| Y[ 4] = 0.1763
| | X[ 5] = 3.4696
| Y[ 5] = 1.7043
| | X[ 6] = 3.4800
| Y[ 6] = 1.7618
| | X[ 7] = 4.6248
| Y[ 7] = 15.4590
| | X[ 8] = 5.1048
| Y[ 8] = 26.8248
| | X[ 9] = 6.2584
| Y[ 9] = 72.9633
| | X[10] = 6.3776
| Y[10] = 79.5120
| |
Вариант 35
x = 3.5232
| X[ 0] = 0.0112
| Y[ 0] = -5.8776
| | X[ 1] = 0.3872
| Y[ 1] = -2.5823
| | X[ 2] = 2.0616
| Y[ 2] = -0.0614
| | X[ 3] = 2.6096
| Y[ 3] = -0.3831
| | X[ 4] = 2.9024
| Y[ 4] = -0.1676
| | X[ 5] = 3.7704
| Y[ 5] = 3.7786
| | X[ 6] = 4.7120
| Y[ 6] = 17.2346
| | X[ 7] = 5.1440
| Y[ 7] = 27.9336
| | X[ 8] = 5.2720
| Y[ 8] = 31.7580
| | X[ 9] = 5.5712
| Y[ 9] = 41.9740
| | X[10] = 6.5008
| Y[10] = 86.6728
| Вариант 36
x = 2.3800
| X[ 0] = 0.2528
| Y[ 0] = -3.5865
| | X[ 1] = 0.4032
| Y[ 1] = -2.4747
| | X[ 2] = 1.1752
| Y[ 2] = 0.2637
| | X[ 3] = 1.5520
| Y[ 3] = 0.3581
| | X[ 4] = 2.1376
| Y[ 4] = -0.1350
| | X[ 5] = 2.9720
| Y[ 5] = -0.0537
| | X[ 6] = 3.4648
| Y[ 6] = 1.6781
| | X[ 7] = 3.8704
| Y[ 7] = 4.6730
| | X[ 8] = 4.4232
| Y[ 8] = 11.8056
| | X[ 9] = 5.7640
| Y[ 9] = 49.5632
| | X[10] = 5.7784
| Y[10] = 50.1632
| Вариант 37
x = 5.6600
| X[ 0] = 0.4784
| Y[ 0] = -2.0013
| | X[ 1] = 1.1832
| Y[ 1] = 0.2719
| | X[ 2] = 1.4496
| Y[ 2] = 0.3837
| | X[ 3] = 1.7648
| Y[ 3] = 0.2222
| | X[ 4] = 2.3184
| Y[ 4] = -0.2861
| | X[ 5] = 3.2760
| Y[ 5] = 0.8016
| | X[ 6] = 3.2872
| Y[ 6] = 0.8455
| | X[ 7] = 3.9392
| Y[ 7] = 5.3532
| | X[ 8] = 5.3472
| Y[ 8] = 34.1540
| | X[ 9] = 5.7224
| Y[ 9] = 47.8562
| | X[10] = 5.9184
| Y[10] = 56.2442
| | Вариант 38
x = 5.6992
| X[ 0] = 0.1568
| Y[ 0] = -4.4189
| | X[ 1] = 0.8560
| Y[ 1] = -0.3532
| | X[ 2] = 0.9824
| Y[ 2] = -0.0361
| | X[ 3] = 1.3416
| Y[ 3] = 0.3730
| | X[ 4] = 2.0608
| Y[ 4] = -0.0606
| | X[ 5] = 2.5928
| Y[ 5] = -0.3845
| | X[ 6] = 2.6928
| Y[ 6] = -0.3603
| | X[ 7] = 4.0056
| Y[ 7] = 6.0618
| | X[ 8] = 4.9128
| Y[ 8] = 21.8006
| | X[ 9] = 4.9344
| Y[ 9] = 22.3328
| | X[10] = 6.0224
| Y[10] = 61.0588
| | Вариант 40
x = 3.1184
| X[ 0] = 0.3176
| Y[ 0] = -3.0796
| | X[ 1] = 0.8832
| Y[ 1] = -0.2761
| | X[ 2] = 1.2264
| Y[ 2] = 0.3106
| | X[ 3] = 2.0560
| Y[ 3] = -0.0558
| | X[ 4] = 2.3616
| Y[ 4] = -0.3143
| | X[ 5] = 2.4472
| Y[ 5] = -0.3578
| | X[ 6] = 3.2992
| Y[ 6] = 0.8937
| | X[ 7] = 3.8472
| Y[ 7] = 4.4557
| | X[ 8] = 4.1920
| Y[ 8] = 8.3403
| | X[ 9] = 5.0080
| Y[ 9] = 24.2086
| | X[10] = 5.3776
| Y[10] = 35.1547
| Вариант 39
x = 2.3768
| X[ 0] = 0.4088
| Y[ 0] = -2.4376
| | X[ 1] = 0.4448
| Y[ 1] = -2.2063
| | X[ 2] = 0.9352
| Y[ 2] = -0.1425
| | X[ 3] = 1.1224
| Y[ 3] = 0.2017
| | X[ 4] = 1.1696
| Y[ 4] = 0.2578
| | X[ 5] = 1.6608
| Y[ 5] = 0.3002
| | X[ 6] = 2.1128
| Y[ 6] = -0.1114
| | X[ 7] = 2.5912
| Y[ 7] = -0.3846
| | X[ 8] = 2.6048
| Y[ 8] = -0.3836
| | X[ 9] = 4.5264
| Y[ 9] = 13.5988
| | X[10] = 5.9016
| Y[10] = 55.4904
| | Варианты различаются между собой конкретным значением точки x, в которой необходимо определить значение функции, а также таблицей задания функции.
|




 в n +1 различных точках
в n +1 различных точках  , которые обозначим следующим образом:
, которые обозначим следующим образом: 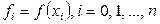 .
. степени n, который в точках
степени n, который в точках 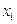 принимает заданные значения, т. е.
принимает заданные значения, т. е. . (1.4)
. (1.4) , то замену функции
, то замену функции  , (1.5)
, (1.5) . (1.6)
. (1.6) (
( - отрезок, содержащий все узлы интерполяции
- отрезок, содержащий все узлы интерполяции 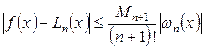 , (1.7)
, (1.7) ;
; 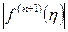 - (n +1)-я производная интерполируемой функции в некоторой точке
- (n +1)-я производная интерполируемой функции в некоторой точке  ;
;  .
.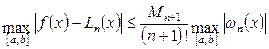 . (1.8)
. (1.8)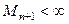 .
.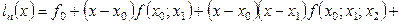 …
…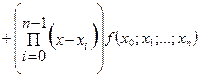 , (1.9)
, (1.9)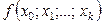 - разделенная разность k -го порядка.
- разделенная разность k -го порядка. ,
, .
. , а не его представление, может быть использована итерационно-интерполяционная схема Эйткена [6], [12].
, а не его представление, может быть использована итерационно-интерполяционная схема Эйткена [6], [12]. - интерполяционный многочлен, определяемый парами
- интерполяционный многочлен, определяемый парами 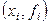 ,
, 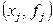 ,
, 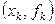 ,... так, что
,... так, что 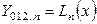 .
.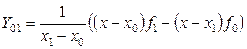 ,
,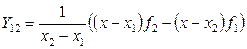 ,
, ,
,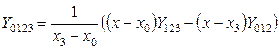 .
.


