Линейных алгебраических уравнений
ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
Методические указания
к лабораторным работам по дисциплине
“ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА”
Санкт-Петербург
Министерство общего и профессионального образования РФ
__________________
Санкт-Петербургский государственный электротехнический
университет
____________________________________________________________
ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ И РЕШЕНИЕ СИСТЕМ
ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
Методические указания
к лабораторным работам по дисциплине
“ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА”
Санкт-Петербург
УДК 519.7
Интерполирование функций и решение систем линейных алгебраических уравнений: Методические указания к лабораторным работам по дисциплине "Вычислительная математика" / Сост.: В.Н. Кафтасьев, А.Р. Лисс, М.С. Титов; СПбГЭТУ. СПб., 1998. 32 с.
Содержат формулировку заданий лабораторных работ и необходимые для их исполнения пояснения. При разработке лабораторных работ особое внимание уделяется вопросам исследования точности и обусловленности применяемых методов машинных вычислений.
Предназначены для студентов ФАВТ направления "Информатика и вычислительная техника" и специальности 220400, а также для студентов других специальностей, изучающих численные методы решения задач на ЭВМ.
Утверждено
редакционно-издательским советом университета
в качестве методических указаний
© СПбГЭТУ, 1998
ВВЕДЕНИЕ
Цикл лабораторных работ предназначен для студентов 2-го курса (четвертый семестр), изучающих дисциплину “Вычислительная математика” и работающих в компьютерных классах на базе ЭВМ типа IBM PC AT-286 и выше, снабженных компилятором языка С (С++). Работы цикла посвящены отработке тем “Интерполирование функций” и “Задачи линейной алгебры”. Каждая из работ ставит целью изучение либо конкретного численного метода, либо набора численных процедур (схем, формул), позволяющих реализовать выполнение одной из классических задач вычислительной математики: интерполирование функций в случаях неравноотстоящих и равноотстоящих узлов и решение систем линейных алгебраических уравнений с использованием различных вычислительных способов. Порядок расположения лабораторных работ в методических указаниях соответствует последовательности изложения лекционного материала. Для углубленного изучения упомянутых задач и методов их решения целесообразно воспользоваться изданиями [1]-[10]. Данные методические указания являются продолжением материала, изложенного авторами в [11].
Выполнять каждую лабораторную работу следует поэтапно в следующем порядке:
- подготовка к решению задачи на персональной ЭВМ (ПЭВМ);
- проведение вычислительного эксперимента на ПЭВМ;
- анализ результатов вычислений;
- оформление отчета.
Подготовка к решению задачи на ПЭВМ производится как вне ком-пьютерного класса, так и непосредственно на ПЭВМ. Она включает:
- ознакомление с описанием работы и заданием для выполнения;
- составление программных модулей, содержащих определенные заданием и персональным вариантом вычислительные процедуры, и/или ввод исходных данных;
- компиляцию разработанных программных модулей, их отладку и сопряжение с имеющимися для большинства работ программами-функциями, реализующими конкретные численные методы;
- планирование вычислительного эксперимента на ПЭВМ в рамках выполняемого задания.
Подпрограммы-функции, предназначенные для применения в процессе вычислений, представлены в виде библиотеки модулей на языке программирования С++. Это предопределяет ориентацию цикла работ на студентов, владеющих данным языком и навыками программирования в необходимом объеме.
Проведение вычислительного эксперимента на ПЭВМ осуществляется в соответствии с порядком выполнения работы и заданием на исследование указанных зависимостей и обусловленности изучаемого метода.
Анализ результатов вычислений заключается в построении исследуемых зависимостей и сравнительной оценке метода (вычислительной процедуры) по характерным для данной группы методов параметрам, например скорости сходимости, степени обусловленности, достижимой точности и т. п.
Анализ результатов и оформление отчета производятся вне компьютерного класса.
Отчет должен содержать:
- постановку задачи;
- тексты разработанных программ;
- результаты вычислений, их теоретический и экспериментальный анализ в виде таблиц и графиков, снабженных необходимыми комментариями;
- развернутые выводы по лабораторной работе.
ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ
Пусть величина 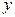 является функцией аргумента является функцией аргумента  . Это означает, что любому значению . Это означает, что любому значению  из области определения поставлено в соответствие значение из области определения поставлено в соответствие значение 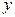 . Однако на практике часто неизвестна связь между . Однако на практике часто неизвестна связь между  и и 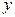 , т. е. невозможно записать эту связь в виде некоторой зависимости , т. е. невозможно записать эту связь в виде некоторой зависимости  . В других случаях при известной зависимости . В других случаях при известной зависимости  ее использование в практических задачах затруднительно (например, она содержит сложные, трудно вычисляемые выражения). ее использование в практических задачах затруднительно (например, она содержит сложные, трудно вычисляемые выражения).
Наиболее распространенным и важным для практического использования случаем, когда вид связи между параметрами  и и 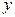 неизвестен, является задание этой связи в виде некоторой таблицы неизвестен, является задание этой связи в виде некоторой таблицы  , в которой дискретному множеству значений аргумента , в которой дискретному множеству значений аргумента 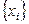 поставлено в соответствие множество значений функции поставлено в соответствие множество значений функции 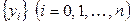 . Эти значения – либо результаты расчетов, либо экспериментальные данные. На практике могут понадобиться значения величины . Эти значения – либо результаты расчетов, либо экспериментальные данные. На практике могут понадобиться значения величины 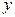 и в других точках, отличных от узлов и в других точках, отличных от узлов 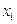 . Таким образом, приходим к необходимости использования имеющихся табличных данных для приближенного вычисления искомого параметра . Таким образом, приходим к необходимости использования имеющихся табличных данных для приближенного вычисления искомого параметра 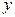 при любом значении (из некоторой области) определяющего параметра при любом значении (из некоторой области) определяющего параметра  , поскольку точная связь , поскольку точная связь  неизвестна. неизвестна.
Этой цели служит задача о приближении (аппроксимации) функций: данную функцию  требуется аппроксимировать (приближенно заменить) некоторой функцией требуется аппроксимировать (приближенно заменить) некоторой функцией  так, чтобы отклонение (в некотором смысле) так, чтобы отклонение (в некотором смысле)  от от  в заданной области было наименьшим. Функция в заданной области было наименьшим. Функция  при этом называется аппроксимирующей. при этом называется аппроксимирующей.
Для практики важен случай аппроксимации функции многочленом
 (1.1) (1.1)
Этот случай, т. е. приближение многочленами, является одной из задач классического численного анализа [3], [4], [8], [10]. Рассмотрим аппроксимацию этого рода и методы ее реализации в вычислительных процедурах на ЭВМ. Коэффициенты 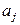 в процедурах подбираются так, чтобы достичь наименьшего отклонения многочлена от данной функции. в процедурах подбираются так, чтобы достичь наименьшего отклонения многочлена от данной функции.
Если приближение строится на заданном дискретном множестве точек 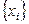 , то аппроксимация называется точечной. Одним из основных типов точечной аппроксимации является интерполирование, которое заключается в следующем: для данной функции , то аппроксимация называется точечной. Одним из основных типов точечной аппроксимации является интерполирование, которое заключается в следующем: для данной функции  строится многочлен (1.1), принимающий в заданных точках строится многочлен (1.1), принимающий в заданных точках 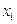 те же значения те же значения 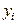 , что и функция , что и функция  , т. е. , т. е.
 (1.2) (1.2)
При данной постановке задачи предполагается, что среди значений 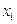 нет одинаковых: нет одинаковых: 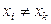 при при 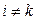 . Точки . Точки 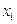 называются узлами интерполяции, а многочлен называются узлами интерполяции, а многочлен  - интерполяционным многочленом. Близость интерполяционного многочлена к заданной функции состоит, таким образом, в том, что их значения совпадают на заданной системе точек (узлов). - интерполяционным многочленом. Близость интерполяционного многочлена к заданной функции состоит, таким образом, в том, что их значения совпадают на заданной системе точек (узлов).
Максимальная степень интерполяционного многочлена 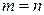 . В этом случае говорят о глобальной интерполяции, так как один многочлен . В этом случае говорят о глобальной интерполяции, так как один многочлен
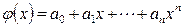 (1.3) (1.3)
используется для интерполяции функции  на всем рассматриваемом интервале изменения аргумента на всем рассматриваемом интервале изменения аргумента  . Коэффициенты . Коэффициенты 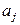 многочлена (1.3) находят из системы уравнений (1.2). Можно показать, что при многочлена (1.3) находят из системы уравнений (1.2). Можно показать, что при 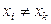 ( (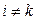 ) эта система имеет единственное решение [1] - [4], [10]. ) эта система имеет единственное решение [1] - [4], [10].
Возможны два случая задания функции  : :
- точки 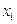 располагаются на оси абсцисс неравномерно на различных расстояниях одна от другой - случай неравноотстоящих узлов; располагаются на оси абсцисс неравномерно на различных расстояниях одна от другой - случай неравноотстоящих узлов;
- точки 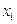 располагаются на оси абсцисс равномерно с фиксирован- ным шагом - случай равноотстоящих узлов. располагаются на оси абсцисс равномерно с фиксирован- ным шагом - случай равноотстоящих узлов.
В каждом из указанных случаев для интерполирования функций применяются различные интерполяционные формулы. Их изучению посвящены, соответственно, лабораторные работы № 9 и № 10. 
Лабораторная работа № 10
В соответствии с заданием, полученным от преподавателя, студентам необходимо разработать программу, обеспечивающую вычисление значения функции в заданных точках с использованием подходящих для каждого конкретного случая интерполяционных формул.
Вариант 2
x1 = 1.5380; x2 = 1.6970;
x3 = 1.3350
| X[ 0] = 0.2620
| Y[ 0] = -0.1810
| | X[ 1] = 0.4190
| Y[ 1] = -0.0450
| | X[ 2] = 0.5770
| Y[ 2] = 0.0100
| | X[ 3] = 0.7340
| Y[ 3] = 0.0090
| | X[ 4] = 0.8920
| Y[ 4] = -0.0260
| | X[ 5] = 1.0490
| Y[ 5] = -0.0720
| | X[ 6] = 1.2070
| Y[ 6] = -0.1050
| | X[ 7] = 1.3640
| Y[ 7] = -0.1020
| | X[ 8] = 1.5220
| Y[ 8] = -0.0380
| | X[ 9] = 1.6790
| Y[ 9] = 0.1060
| | X[10] = 1.8370
| Y[10] = 0.3600
| | Используя подходящую интерполяционную формулу, вычислите в точках x 1, x 2, x 3 значения функции, заданной таблицей, для узлов с равноотстоящим шагом.
Вариант 1
x1 = 1.2120; x2 = 1.4790;
x3 = 1.0150
| X[ 0] = 0.2560
| Y[ 0] = -0.1680
| | X[ 1] = 0.4090
| Y[ 1] = -0.0420
| | X[ 2] = 0.5630
| Y[ 2] = 0.0100
| | X[ 3] = 0.7170
| Y[ 3] = 0.0080
| | X[ 4] = 0.8710
| Y[ 4] = -0.0240
| | X[ 5] = 1.0240
| Y[ 5] = -0.0670
| | X[ 6] = 1.1780
| Y[ 6] = -0.0970
| | X[ 7] = 1.3320
| Y[ 7] = -0.0940
| | X[ 8] = 1.4860
| Y[ 8] = -0.0350
| | X[ 9] = 1.6390
| Y[ 9] = 0.0990
| | X[10] = 1.7930
| Y[10] = 0.3350
| |
Вариант 3
x1 = 0.8110; x2=0.3770;
x3=1.5480
| X[ 0] = 0.2680
| Y[ 0] = -0.1950
| | X[ 1] = 0.4290
| Y[ 1] = -0.0480
| | X[ 2] = 0.5910
| Y[ 2] = 0.0110
| | X[ 3] = 0.7520
| Y[ 3] = 0.0100
| | X[ 4] = 0.9130
| Y[ 4] = -0.0280
| | X[ 5] = 1.0740
| Y[ 5] = -0.0770
| | X[ 6] = 1.2360
| Y[ 6] = -0.1130
| | X[ 7] = 1.3970
| Y[ 7] = -0.1090
| | X[ 8] = 1.5580
| Y[ 8] = -0.0410
| | X[ 9] = 1.7190
| Y[ 9] = 0.1140
| | X[10] = 1.8810
| Y[10] = 0.3870
| Вариант 4
x1 = 1.2230; x2=1.6830;
x3=1.7640
| X[ 0] = 0.2740
| Y[ 0] = -0.2090
| | X[ 1] = 0.4390
| Y[ 1] = -0.0510
| | X[ 2] = 0.6040
| Y[ 2] = 0.0120
| | X[ 3] = 0.7690
| Y[ 3] = 0.0100
| | X[ 4] = 0.9340
| Y[ 4] = -0.0290
| | X[ 5] = 1.0990
| Y[ 5] = -0.0820
| | X[ 6] = 1.2640
| Y[ 6] = -0.1200
| | X[ 7] = 1.4290
| Y[ 7] = -0.1170
| | X[ 8] = 1.5940
| Y[ 8] = -0.0440
| | X[ 9] = 1.7590
| Y[ 9] = 0.1230
| | X[10] = 1.9240
| Y[10] = 0.4130
| Вариант 6
x1 = 1.0980; x2 = 1.8770;
x3 = 1.5130
| X[ 0] = 0.2870
| Y[ 0] = -0.2380
| | X[ 1] = 0.4590
| Y[ 1] = -0.0590
| | X[ 2] = 0.6320
| Y[ 2] = 0.0140
| | X[ 3] = 0.8040
| Y[ 3] = 0.0120
| | X[ 4] = 0.9770
| Y[ 4] = -0.0340
| | X[ 5] = 1.1490
| Y[ 5] = -0.0940
| | X[ 6] = 1.3220
| Y[ 6] = -0.1380
| | X[ 7] = 1.4940
| Y[ 7] = -0.1340
| | X[ 8] = 1.6670
| Y[ 8] = -0.0500
| | X[ 9] = 1.8390
| Y[ 9] = 0.1400
| | X[10] = 2.0120
| Y[10] = 0.4740
| Вариант 7
x1 = 1.4980; x2 = 0.4120;
x3 = 1.6840
| X[ 0] = 0.2930
| Y[ 0] = -0.2540
| | X[ 1] = 0.4690
| Y[ 1] = -0.0630
| | X[ 2] = 0.6460
| Y[ 2] = 0.0150
| | X[ 3] = 0.8220
| Y[ 3] = 0.0130
| | X[ 4] = 0.9980
| Y[ 4] = -0.0360
| | X[ 5] = 1.1740
| Y[ 5] = -0.1010
| | X[ 6] = 1.3510
| Y[ 6] = -0.1470
| | X[ 7] = 1.5270
| Y[ 7] = -0.1420
| | X[ 8] = 1.7030
| Y[ 8] = -0.0540
| | X[ 9] = 1.8790
| Y[ 9] = 0.1500
| | X[10] = 2.0560
| Y[10] = 0.5060
| Вариант 8
x1 = 1.4870; x2 = 0.5090;
x3 = 1.4530
| X[ 0] = 0.2990
| Y[ 0] = -0.2710
| | X[ 1] = 0.4790
| Y[ 1] = -0.0670
| | X[ 2] = 0.6590
| Y[ 2] = 0.0160
| | X[ 3] = 0.8390
| Y[ 3] = 0.0140
| | X[ 4] = 1.0190
| Y[ 4] = -0.0380
| | X[ 5] = 1.1990
| Y[ 5] = -0.1070
| | X[ 6] = 1.3790
| Y[ 6] = -0.1570
| | X[ 7] = 1.5590
| Y[ 7] = -0.1520
| | X[ 8] = 1.7390
| Y[ 8] = -0.0580
| | X[ 9] = 1.9190
| Y[ 9] = 0.1590
| | X[10] = 2.0990
| Y[10] = 0.5370
| |
Вариант 5
x1 = 1.2510; x2 = 1.1700;
x3 = 1.0870
| X[ 0] = 0.2810
| Y[ 0] = -0.2220
| | X[ 1] = 0.4490
| Y[ 1] = -0.0550
| | X[ 2] = 0.6180
| Y[ 2] = 0.0130
| | X[ 3] = 0.7870
| Y[ 3] = 0.0110
| | X[ 4] = 0.9560
| Y[ 4] = -0.0320
| | X[ 5] = 1.1240
| Y[ 5] = -0.0880
| | X[ 6] = 1.2930
| Y[ 6] = -0.1290
| | X[ 7] = 1.4620
| Y[ 7] = -0.1250
| | X[ 8] = 1.6310
| Y[ 8] = -0.0470
| | X[ 9] = 1.7990
| Y[ 9] = 0.1310
| | X[10] = 1.9680
| Y[10] = 0.4430
| |
Вариант 9
x1 = 1.0530; x2 = 0.4450;
x3 = 1.1550
| X[ 0] = 0.3060
| Y[ 0] = -0.2870
| | X[ 1] = 0.4890
| Y[ 1] = -0.0710
| | X[ 2] = 0.6730
| Y[ 2] = 0.0170
| | X[ 3] = 0.8570
| Y[ 3] = 0.0140
| | X[ 4] = 1.0410
| Y[ 4] = -0.0410
| | X[ 5] = 1.2240
| Y[ 5] = -0.1140
| | X[ 6] = 1.4080
| Y[ 6] = -0.1670
| | X[ 7] = 1.5920
| Y[ 7] = -0.1610
| | X[ 8] = 1.7760
| Y[ 8] = -0.0610
| | X[ 9] = 1.9590
| Y[ 9] = 0.1700
| | X[10] = 2.1430
| Y[10] = 0.5720
| Вариант 11
x1 = 1.1600; x2 = 2.1660;
x3 = 1.4620
| X[ 0] = 0.3180
| Y[ 0] = -0.3250
| | X[ 1] = 0.5090
| Y[ 1] = -0.0800
| | X[ 2] = 0.7010
| Y[ 2] = 0.0190
| | X[ 3] = 0.8920
| Y[ 3] = 0.0160
| | X[ 4] = 1.0830
| Y[ 4] = -0.0460
| | X[ 5] = 1.2740
| Y[ 5] = -0.1290
| | X[ 6] = 1.4660
| Y[ 6] = -0.1880
| | X[ 7] = 1.6570
| Y[ 7] = -0.1820
| | X[ 8] = 1.8480
| Y[ 8] = -0.0690
| | X[ 9] = 2.0390
| Y[ 9] = 0.1910
| | X[10] = 2.2310
| Y[10] = 0.6460
| Вариант 10
x1 = 1.3020; x2 = 1.5690;
x3 = 1.8350
| X[ 0] = 0.3120
| Y[ 0] = -0.3060
| | X[ 1] = 0.4990
| Y[ 1] = -0.0760
| | X[ 2] = 0.6870
| Y[ 2] = 0.0180
| | X[ 3] = 0.8740
| Y[ 3] = 0.0150
| | X[ 4] = 1.0620
| Y[ 4] = -0.0440
| | X[ 5] = 1.2490
| Y[ 5] = -0.1210
| | X[ 6] = 1.4370
| Y[ 6] = -0.1770
| | X[ 7] = 1.6240
| Y[ 7] = -0.1720
| | X[ 8] = 1.8120
| Y[ 8] = -0.0650
| | X[ 9] = 1.9990
| Y[ 9] = 0.1800
| | X[10] = 2.1870
| Y[10] = 0.6080
| Вариант 13
x1 = 0.6190; x2 = 1.3990;
x3 = 1.1000
| X[ 0] = 0.3310
| Y[ 0] = -0.3630
| | X[ 1] = 0.5290
| Y[ 1] = -0.0900
| | X[ 2] = 0.7280
| Y[ 2] = 0.0210
| | X[ 3] = 0.9270
| Y[ 3] = 0.0180
| | X[ 4] = 1.1260
| Y[ 4] = -0.0520
| | X[ 5] = 1.3240
| Y[ 5] = -0.1440
| | X[ 6] = 1.5230
| Y[ 6] = -0.2110
| | X[ 7] = 1.7220
| Y[ 7] = -0.2040
| | X[ 8] = 1.9210
| Y[ 8] = -0.0770
| | X[ 9] = 2.1190
| Y[ 9] = 0.2150
| | X[10] = 2.3180
| Y[10] = 0.7240
| Вариант 14
x1 = 1.6510; x2 = 1.3870;
x3 = 2.2260
| X[ 0] = 0.3370
| Y[ 0] = -0.3850
| | X[ 1] = 0.5390
| Y[ 1] = -0.0950
| | X[ 2] = 0.7420
| Y[ 2] = 0.0230
| | X[ 3] = 0.9440
| Y[ 3] = 0.0190
| | X[ 4] = 1.1470
| Y[ 4] = -0.0550
| | X[ 5] = 1.3490
| Y[ 5] = -0.1530
| | X[ 6] = 1.5520
| Y[ 6] = -0.2230
| | X[ 7] = 1.7540
| Y[ 7] = -0.2160
| | X[ 8] = 1.9570
| Y[ 8] = -0.0820
| | X[ 9] = 2.1590
| Y[ 9] = 0.2270
| | X[10] = 2.3620
| Y[10] = 0.7670
| |
Вариант 12
x1 = 1.6960; x2 = 1.8860;
x3 = 1.3400
| X[ 0] = 0.3240
| Y[ 0] = -0.3450
| | X[ 1] = 0.5190
| Y[ 1] = -0.0850
| | X[ 2] = 0.7140
| Y[ 2] = 0.0200
| | X[ 3] = 0.9090
| Y[ 3] = 0.0170
| | X[ 4] = 1.1040
| Y[ 4] = -0.0490
| | X[ 5] = 1.2990
| Y[ 5] = -0.1360
| | X[ 6] = 1.4940
| Y[ 6] = -0.1990
| | X[ 7] = 1.6890
| Y[ 7] = -0.1930
| | X[ 8] = 1.8840
| Y[ 8] = -0.0740
| | X[ 9] = 2.0790
| Y[ 9] = 0.2030
| | X[10] = 2.2740
| Y[10] = 0.6830
| |
Вариант 17
x1 = 1.5610; x2 = 1.7840;
x3=2.1280
| X[ 0] = 0.3560
| Y[ 0] = -0.4520
| | X[ 1] = 0.5690
| Y[ 1] = -0.1120
| | X[ 2] = 0.7830
| Y[ 2] = 0.0270
| | X[ 3] = 0.9970
| Y[ 3] = 0.0230
| | X[ 4] = 1.2110
| Y[ 4] = -0.0650
| | X[ 5] = 1.4240
| Y[ 5] = -0.1800
| | X[ 6] = 1.6380
| Y[ 6] = -0.2630
| | X[ 7] = 1.8520
| Y[ 7] = -0.2540
| | X[ 8] = 2.0660
| Y[ 8] = -0.0960
| | X[ 9] = 2.2790
| Y[ 9] = 0.2680
| | X[10] = 2.4930
| Y[10] = 0.9010
| Вариант 15
x1 = 0.6070; x2 = 1.6230;
x3 = 0.8430
| X[ 0] = 0.3430
| Y[ 0] = -0.4070
| | X[ 1] = 0.5490
| Y[ 1] = -0.1010
| | X[ 2] = 0.7560
| Y[ 2] = 0.0240
| | X[ 3] = 0.9620
| Y[ 3] = 0.0200
| | X[ 4] = 1.1680
| Y[ 4] = -0.0580
| | X[ 5] = 1.3740
| Y[ 5] = -0.1620
| | X[ 6] = 1.5810
| Y[ 6] = -0.2360
| | X[ 7] = 1.7870
| Y[ 7] = -0.2280
| | X[ 8] = 1.9930
| Y[ 8] = -0.0870
| | X[ 9] = 2.1990
| Y[ 9] = 0.2400
| | X[10] = 2.4060
| Y[10] = 0.8110
| Вариант 16
x1 = 2.2960; x2 = 0.9390;
x3 = 1.3920
| X[ 0] = 0.3490
| Y[ 0] = -0.4300
| | X[ 1] = 0.5590
| Y[ 1] = -0.1060
| | X[ 2] = 0.7690
| Y[ 2] = 0.0250
| | X[ 3] = 0.9790
| Y[ 3] = 0.0220
| | X[ 4] = 1.1890
| Y[ 4] = -0.0610
| | X[ 5] = 1.3990
| Y[ 5] = -0.1710
| | X[ 6] = 1.6090
| Y[ 6] = -0.2490
| | X[ 7] = 1.8190
| Y[ 7] = -0.2410
| | X[ 8] = 2.0290
| Y[ 8] = -0.0920
| | X[ 9] = 2.2390
| Y[ 9] = 0.2540
| | X[10] = 2.4490
| Y[10] = 0.8530
| Вариант 18
x1 = 0.7600; x2 = 2.0620;
x3=1.7640
| X[ 0] = 0.3620
| Y[ 0] = -0.4770
| | X[ 1] = 0.5790
| Y[ 1] = -0.1180
| | X[ 2] = 0.7970
| Y[ 2] = 0.0280
| | X[ 3] = 1.0140
| Y[ 3] = 0.0240
| | X[ 4] = 1.2320
| Y[ 4] = -0.0690
| | X[ 5] = 1.4490
| Y[ 5] = -0.1900
| | X[ 6] = 1.6670
| Y[ 6] = -0.2770
| | X[ 7] = 1.8840
| Y[ 7] = -0.2680
| | X[ 8] = 2.1020
| Y[ 8] = -0.1010
| | X[ 9] = 2.3190
| Y[ 9] = 0.2820
| | X[10] = 2.5370
| Y[10] = 0.9500
| Вариант 19
x1 = 2.0690; x2 = 2.0390;
x3=1.6990
| X[ 0] = 0.3680
| Y[ 0] = -0.5030
| | X[ 1] = 0.5890
| Y[ 1] = -0.1240
| | X[ 2] = 0.8110
| Y[ 2] = 0.0300
| | X[ 3] = 1.0320
| Y[ 3] = 0.0250
| | X[ 4] = 1.2530
| Y[ 4] = -0.0720
| | X[ 5] = 1.4740
| Y[ 5] = -0.2000
| | X[ 6] = 1.6960
| Y[ 6] = -0.2910
| | X[ 7] = 1.9170
| Y[ 7] = -0.2820
| | X[ 8] = 2.1380
| Y[ 8] = -0.1070
| | X[ 9] = 2.3590
| Y[ 9] = 0.2970
| | X[10] = 2.5810
| Y[10] = 1.0010
| Вариант 20
x1 = 1.5370; x2 = 1.7030;
x3=1.7400
| X[ 0] = 0.3740
| Y[ 0] = -0.5290
| | X[ 1] = 0.5990
| Y[ 1] = -0.1310
| | X[ 2] = 0.8240
| Y[ 2] = 0.0310
| | X[ 3] = 1.0490
| Y[ 3] = 0.0270
| | X[ 4] = 1.2740
| Y[ 4] = -0.0760
| | X[ 5] = 1.4990
| Y[ 5] = -0.2100
| | X[ 6] = 1.7240
| Y[ 6] = -0.3060
| | X[ 7] = 1.9490
| Y[ 7] = -0.2970
| | X[ 8] = 2.1740
| Y[ 8] = -0.1130
| | X[ 9] = 2.3990
| Y[ 9] = 0.3130
| | X[10] = 2.6240
| Y[10] = 1.0500
| |
Вариант 22
x1= 1.4510; x2 = 0.9480;
x3 = 2.4550
| X[ 0] = 0.3870
| Y[ 0] = -0.5830
| | X[ 1] = 0.6190
| Y[ 1] = -0.1440
| | X[ 2] = 0.8520
| Y[ 2] = 0.0350
| | X[ 3] = 1.0840
| Y[ 3] = 0.0300
| | X[ 4] = 1.3170
| Y[ 4] = -0.0840
| | X[ 5] = 1.5490
| Y[ 5] = -0.2320
| | X[ 6] = 1.7820
| Y[ 6] = -0.3380
| | X[ 7] = 2.0140
| Y[ 7] = -0.3280
| | X[ 8] = 2.2470
| Y[ 8] = -0.1240
| | X[ 9] = 2.4790
| Y[ 9] = 0.3450
| | X[10] = 2.7120
| Y[10] = 1.1610
| Вариант 26
x1 = 1.3780; x2 = 1.4350;
x3=1.7020
| X[ 0] = 0.4120
| Y[ 0] = -0.7030
| | X[ 1] = 0.6590
| Y[ 1] = -0.1740
| | X[ 2] = 0.9070
| Y[ 2] = 0.0420
| | X[ 3] = 1.1540
| Y[ 3] = 0.0360
| | X[ 4] = 1.4020
| Y[ 4] = -0.1010
| | X[ 5] = 1.6490
| Y[ 5] = -0.2800
| | X[ 6] = 1.8970
| Y[ 6] = -0.4080
| | X[ 7] = 2.1440
| Y[ 7] = -0.3950
| | X[ 8] = 2.3920
| Y[ 8] = -0.1500
| | X[ 9] = 2.6390
| Y[ 9] = 0.4160
| | X[10] = 2.8870
| Y[10] = 1.4010
| Вариант 21
x1 = 1.6790; x2 = 2.2880;
x3 = 2.3860
| X[ 0] = 0.3810
| Y[ 0] = -0.5540
| | X[ 1] = 0.6090
| Y[ 1] = -0.1370
| | X[ 2] = 0.8380
| Y[ 2] = 0.0330
| | X[ 3] = 1.0670
| Y[ 3] = 0.0280
| | X[ 4] = 1.2960
| Y[ 4] = -0.0800
| | X[ 5] = 1.5240
| Y[ 5] = -0.2210
| | X[ 6] = 1.7530
| Y[ 6] = -0.3220
| | X[ 7] = 1.9820
| Y[ 7] = -0.3120
| | X[ 8] = 2.2110
| Y[ 8] = -0.1180
| | X[ 9] = 2.4390
| Y[ 9] = 0.3280
| | X[10] = 2.6680
| Y[10] = 1.1050
| Вариант 24
x1 = 2.5030; x2 = 0.9080;
x3 = 0.5840
| X[ 0] = 0.3990
| Y[ 0] = -0.6420
| | X[ 1] = 0.6390
| Y[ 1] = -0.1590
| | X[ 2] = 0.8790
| Y[ 2] = 0.0380
| | X[ 3] = 1.1190
| Y[ 3] = 0.0330
| | X[ 4] = 1.3590
| Y[ 4] = -0.0920
| | X[ 5] = 1.5990
| Y[ 5] = -0.2550
| | X[ 6] = 1.8390
| Y[ 6] = -0.3720
| | X[ 7] = 2.0790
| Y[ 7] = -0.3600
| | X[ 8] = 2.3190
| Y[ 8] = -0.1370
| | X[ 9] = 2.5590
| Y[ 9] = 0.3800
| | X[10] = 2.7990
| Y[10] = 1.2750
| Вариант 23
x1 = 1.4590; x2 = 1.4070;
x3=1.3350
| X[ 0] = 0.3930
| Y[ 0] = -0.6120
| | X[ 1] = 0.6290
| Y[ 1] = -0.1510
| | X[ 2] = 0.8660
| Y[ 2] = 0.0370
| | X[ 3] = 1.1020
| Y[ 3] = 0.0310
| | X[ 4] = 1.3380
| Y[ 4] = -0.0880
| | X[ 5] = 1.5740
| Y[ 5] = -0.2430
| | X[ 6] = 1.8110
| Y[ 6] = -0.3550
| | X[ 7] = 2.0470
| Y[ 7] = -0.3440
| | X[ 8] = 2.2830
| Y[ 8] = -0.1300
| | X[ 9] = 2.5190
| Y[ 9] = 0.3620
| | X[10] = 2.7560
| Y[10] = 1.2190
| Вариант 25
x1 = 1.7570; x2 = 0.4700;
x3=1.5810
| X[ 0] = 0.4060
| Y[ 0] = -0.6710
| | X[ 1] = 0.6490
| Y[ 1] = -0.1660
| | X[ 2] = 0.8930
| Y[ 2] = 0.0400
| | X[ 3] = 1.1370
| Y[ 3] = 0.0340
| | X[ 4] = 1.3810
| Y[ 4] = -0.0970
| | X[ 5] = 1.6240
| Y[ 5] = -0.2670
| | X[ 6] = 1.8680
| Y[ 6] = -0.3900
| | X[ 7] = 2.1120
| Y[ 7] = -0.3770
| | X[ 8] = 2.3560
| Y[ 8] = -0.1430
| | X[ 9] = 2.5990
| Y[ 9] = 0.3980
| | X[10] = 2.8430
| Y[10] = 1.3370
| |
Вариант 31
x1 = 1.3010; x2 = 2.2450;
x3 = 2.1200
| X[ 0] = 0.4560
| Y[ 0] = -0.9500
| | X[ 1] = 0.7290
| Y[ 1] = -0.2350
| | X[ 2] = 1.0030
| Y[ 2] = 0.0570
| | X[ 3] = 1.2770
| Y[ 3] = 0.0480
| | X[ 4] = 1.5510
| Y[ 4] = -0.1380
| | X[ 5] = 1.8240
| Y[ 5] = -0.3790
| | X[ 6] = 2.0980
| Y[ 6] = -0.5520
| | X[ 7] = 2.3720
| Y[ 7] = -0.5350
| | X[ 8] = 2.6460
| Y[ 8] = -0.2020
| | X[ 9] = 2.9190
| Y[ 9] = 0.5640
| | X[10] = 3.1930
| Y[10] = 1.8940
| Вариант 32
x1 = 2.7820; x2 = 1.3080;
x3 = 2.2850
| X[ 0] = 0.4620
| Y[ 0] = -0.9910
| | X[ 1] = 0.7390
| Y[ 1] = -0.2450
| | X[ 2] = 1.0170
| Y[ 2] = 0.0590
| | X[ 3] = 1.2940
| Y[ 3] = 0.0510
| | X[ 4] = 1.5720
| Y[ 4] = -0.1430
| | X[ 5] = 1.8490
| Y[ 5] = -0.3940
| | X[ 6] = 2.1270
| Y[ 6] = -0.5750
| | X[ 7] = 2.4040
| Y[ 7] = -0.5570
| | X[ 8] = 2.6820
| Y[ 8] = -0.2110
| | X[ 9] = 2.9590
| Y[ 9] = 0.5880
| | X[10] = 3.2370
| Y[10] = 1.9750
| Вариант 28
x1 = 2.2070; x2 = 2.0030;
x3 = 0.5900
| X[ 0] = 0.4240
| Y[ 0] = -0.7700
| | X[ 1] = 0.6790
| Y[ 1] = -0.1900
| | X[ 2] = 0.9340
| Y[ 2] = 0.0460
| | X[ 3] = 1.1890
| Y[ 3] = 0.0390
| | X[ 4] = 1.4440
| Y[ 4] = -0.1110
| | X[ 5] = 1.6990
| Y[ 5] = -0.3060
| | X[ 6] = 1.9540
| Y[ 6] = -0.4460
| | X[ 7] = 2.2090
| Y[ 7] = -0.4320
| | X[ 8] = 2.4640
| Y[ 8] = -0.1650
| | X[ 9] = 2.7190
| Y[ 9] = 0.4560
| | X[10] = 2.9740
| Y[10] = 1.5300
| |
Вариант 38
x1 = 3.3870; x2 = 1.6760;
x3 = 1.2680
| X[ 0] = 0.4990
| Y[ 0] = -1.2540
| | X[ 1] = 0.7990
| Y[ 1] = -0.3100
| | X[ 2] = 1.0990
| Y[ 2] = 0.0750
| | X[ 3] = 1.3990
| Y[ 3] = 0.0640
| | X[ 4] = 1.6990
| Y[ 4] = -0.1800
| | X[ 5] = 1.9990
| Y[ 5] = -0.4980
| | X[ 6] = 2.2990
| Y[ 6] = -0.7270
| | X[ 7] = 2.5990
| Y[ 7] = -0.7040
| | X[ 8] = 2.8990
| Y[ 8] = -0.2680
| | X[ 9] = 3.1990
| Y[ 9] = 0.7430
| | X[10] = 3.4990
| Y[10] = 2.4920
| Вариант 37
x1 = 3.2430; x2 = 3.2460;
x3 = 2.6270
| X[ 0] = 0.4930
| Y[ 0] = -1.2060
| | X[ 1] = 0.7890
| Y[ 1] = -0.2980
| | X[ 2] = 1.0860
| Y[ 2] = 0.0730
| | X[ 3] = 1.3820
| Y[ 3] = 0.0610
| | X[ 4] = 1.6780
| Y[ 4] = -0.1740
| | X[ 5] = 1.9740
| Y[ 5] = -0.4800
| | X[ 6] = 2.2710
| Y[ 6] = -0.7000
| | X[ 7] = 2.5670
| Y[ 7] = -0.6780
| | X[ 8] = 2.8630
| Y[ 8] = -0.2570
| | X[ 9] = 3.1590
| Y[ 9] = 0.7150
| | X[10] = 3.4560
| Y[10] = 2.4050
| Вариант 36
x1 = 1.7310; x2 = 0.5420;
x3 = 3.0450
| X[ 0] = 0.4870
| Y[ 0] = -1.1600
| | X[ 1] = 0.7790
| Y[ 1] = -0.2870
| | X[ 2] = 1.0720
| Y[ 2] = 0.0700
| | X[ 3] = 1.3640
| Y[ 3] = 0.0590
| | X[ 4] = 1.6570
| Y[ 4] = -0.1680
| | X[ 5] = 1.9490
| Y[ 5] = -0.4620
| | X[ 6] = 2.2420
| Y[ 6] = -0.6740
| | X[ 7] = 2.5340
| Y[ 7] = -0.6530
| | X[ 8] = 2.8270
| Y[ 8] = -0.2470
| | X[ 9] = 3.1190
| Y[ 9] = 0.6890
| | X[10] = 3.4120
| Y[10] = 2.3130
| Вариант 34
x1 = 1.7330; x2 = 3.1310;
x3 = 1.8920
| X[ 0] = 0.4740
| Y[ 0] = -1.0750
| | X[ 1] = 0.7590
| Y[ 1] = -0.2650
| | X[ 2] = 1.0440
| Y[ 2] = 0.0640
| | X[ 3] = 1.3290
| Y[ 3] = 0.0550
| | X[ 4] = 1.6140
| Y[ 4] = -0.1550
| | X[ 5] = 1.8990
| Y[ 5] = -0.4270
| | X[ 6] = 2.1840
| Y[ 6] = -0.6230
| | X[ 7] = 2.4690
| Y[ 7] = -0.6040
| | X[ 8] = 2.7540
| Y[ 8] = -0.2300
| | X[ 9] = 3.0390
| Y[ 9] = 0.6370
| | X[10] = 3.3240
| Y[10] = 2.1360
| Вариант 33
x1 = 2.0180; x2 = 3.1920;
x3 = 3.2050
| X[ 0] = 0.4680
| Y[ 0] = -1.0320
| | X[ 1] = 0.7490
| Y[ 1] = -0.2550
| | X[ 2] = 1.0310
| Y[ 2] = 0.0620
| | X[ 3] = 1.3120
| Y[ 3] = 0.0520
| | X[ 4] = 1.5930
| Y[ 4] = -0.1490
| | X[ 5] = 1.8740
| Y[ 5] = -0.4110
| | X[ 6] = 2.1560
| Y[ 6] = -0.5990
| | X[ 7] = 2.4370
| Y[ 7] = -0.5800
| | X[ 8] = 2.7180
| Y[ 8] = -0.2200
| | X[ 9] = 2.9990
| Y[ 9] = 0.6120
| | X[10] = 3.2810
| Y[10] = 2.0580
| Вариант 35
x1 = 1.1710; x2 = 1.4190;
x3 = 1.8680
| X[ 0] = 0.4810
| Y[ 0] = -1.1150
| | X[ 1] = 0.7690
| Y[ 1] = -0.2760
| | X[ 2] = 1.0580
| Y[ 2] = 0.0670
| | X[ 3] = 1.3470
| Y[ 3] = 0.0570
| | X[ 4] = 1.6360
| Y[ 4] = -0.1620
| | X[ 5] = 1.9240
| Y[ 5] = -0.4440
| | X[ 6] = 2.2130
| Y[ 6] = -0.6480
| | X[ 7] = 2.5020
| Y[ 7] = -0.6280
| | X[ 8] = 2.7910
| Y[ 8] = -0.2370
| | X[ 9] = 3.0790
| Y[ 9] = 0.6620
| | X[10] = 3.3680
| Y[10] = 2.2240
| |
Лабораторная работа № 11
В ходе выполнения работы студенты должны найти решение системы линейных уравнений с n неизвестными, заданной матрицей коэффициентов  и вектором свободных членов и вектором свободных членов 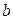 , методом Гаусса. Выполнение работы состоит из следующих этапов: , методом Гаусса. Выполнение работы состоит из следующих этапов:
1) с помощью преподавателя определить систему уравнений, которую нужно решить;
2) для решения системы уравнений разработать программу на языке C, использующую подпрограмму-функцию GAUSS из файла GAUSS.CPP. Данная функция имеет следующие параметры:
- a - матрица коэффициентов системы уравнений размера  , тип , тип 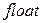 ; ;
- 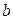 - вектор свободных членов размера - вектор свободных членов размера 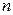 , тип , тип 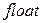 ; ;
-  - выходной вектор результата решения размера - выходной вектор результата решения размера 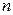 , тип , тип 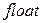 ; ;
- 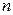 - размер системы (матрицы a и вектора свободных членов - размер системы (матрицы a и вектора свободных членов 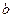 ), тип ), тип 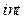 . .
В разрабатываемой программе должна быть описана константа n max, равная максимальным размерам используемых матриц и векторов. Функция GAUSS в качестве значения типа 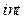 возвращает: возвращает:
а) 0 - в случае нормального завершения процесса вычисления;
б) 1 - в случае вырожденности матрицы а;
в) 2 - если 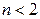 ; ;
г) 3 - если 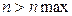 . .
Провести вычисления с использованием разработанной программы и исследовать обусловленность задачи с использованием пакета Matlab, при этом для определения числа обусловленности матрицы A рекомендуется использовать функцию cond(A) [14]. Кроме того, для проверки получаемых результатов можно провести вычисления с помощью пакетов Matlab и Derive [15].
Итерации
Рассматривается система уравнений вида
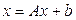 , (2.3) , (2.3)
где  - заданная числовая квадратная матрица n -го порядка, а b - заданный вектор (свободный член). Метод простой итерации состоит в следующем. Выбирается произвольный вектор x (начальное приближение), и строится итерационная последовательность векторов по формуле - заданная числовая квадратная матрица n -го порядка, а b - заданный вектор (свободный член). Метод простой итерации состоит в следующем. Выбирается произвольный вектор x (начальное приближение), и строится итерационная последовательность векторов по формуле
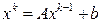 , (2.4) , (2.4)
где k =1, 2, …
Доказана теорема, что если норма  , то система уравнений (2.3) имеет единственное решение , то система уравнений (2.3) имеет единственное решение  и итерации (2.4) сходятся к решению со скоростью геометрической прогрессии [13]. Для оценки погрешности k -го приближения широко применяется неравенство и итерации (2.4) сходятся к решению со скоростью геометрической прогрессии [13]. Для оценки погрешности k -го приближения широко применяется неравенство
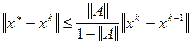 , (2.5) , (2.5)
которое может быть использовано для принятия решения об останове итерационного процесса при выполнении условия
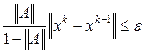 , ,
где 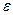 - некоторая заданная погрешность вычислений. - некоторая заданная погрешность вычислений.
Лабораторная работа № 12
В работе студенты должны найти решение системы линейных уравнений с n неизвестными, заданной матрицей коэффициентов  и вектором свободных членов b, методом простых итераций. Выполнение работы включает следующие этапы: и вектором свободных членов b, методом простых итераций. Выполнение работы включает следующие этапы:
1) с помощью преподавателя определить систему уравнений, которую нужно решить. Привести исходную систему к виду (2.3), пригодному для использования метода простых итераций;
2) задать необходимую точность получения результата (количество знаков мантиссы числа);
3) разработать программу решения задачи на языке С с использованием подпрограммы-функции MITER из файла MITER.CPP. Функция MITER имеет следующие параметры:
-  - матрица коэффициентов преобразованной к виду (2.3) системы уравнений размера - матрица коэффициентов преобразованной к виду (2.3) системы уравнений размера  , тип , тип 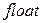 ; ;
- 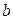 - вектор свободных членов преобразованной системы размера - вектор свободных членов преобразованной системы размера 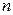 , тип , тип 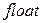 ; ;
-  - полученный в результате проведения итераций вектор решения размера - полученный в результате проведения итераций вектор решения размера 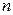 , тип , тип 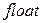 ; ;
- 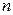 - размер системы уравнений, тип - размер системы уравнений, тип 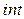 ; ;
-  - количество знаков после запятой в мантиссе результата, остающихся после округления, тип - количество знаков после запятой в мантиссе результата, остающихся после округления, тип 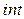 , , 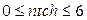 ; ;
- it - выходной параметр, равный количеству произведенных итераций, тип int.
В качестве значения функции типа 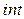 возвращается одно из следующих значений: возвращается одно из следующих значений:
а) 0 - все нормально, получено решение  ; ;
б) 1 - не выполняются условия сходимости итерационного процесса;
в) 2 - размер 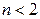 ; ;
г) 3 - значение 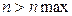 . .
Константа 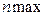 должна быть задана при разработке головной программы аналогично тому, как это делается при выполнении лабораторной работы № 11; должна быть задана при разработке головной программы аналогично тому, как это делается при выполнении лабораторной работы № 11;
4) произвести вычисления с использованием разработанной программы и построить график зависимости числа итераций от задаваемой точности.
Алгебраических уравнений
Файл GAUSS.CPP.
// Подключение математики:
#include <math.h>
// Математика подключена.
gauss(a,b,x,n)
float a[][nmax]; // Исходная матрица коэффицентов:a
float b[]; // Правые части
float x[]; // Результат (будет получен при решении)
int n; // Количество элементов в векторах и размерность матрицы
{
int i,j,k,imax;
int nm1=n-1; // Используется для удобства вместо n, так как
// элементы массивов отсчитываются с 0, а не с 1
int err=0; // Начальное значение кода ошибки =0 (т.е. ошибки нет),
// перед окончанием функции переменная err передается
// в качестве значения функции
float amax,t,mi,sum;
// Проверка корректности переменной n и константы nmax
// в случае противоречий выход из функции:
// endofproc -метка конца функции
if (n<2) { err=2; goto endofproc; } // В матрице <2 элементов
if (n>nmax) { err=3; goto endofproc; }
// n>реальной размерности =nmax
// Теперь все корректно.
// Далее следует...
// Цикл из n-1 шагов, на каждом шаге находится главный элемент и
// преобразовывается матрица.
// Главный элемент определяется только из очередного столбца,
// а не из всей матрицы.
// n-й шаг цикла не нужен так как остается один элемент a[n-1][n-1],
// который сам по себе главный (рассматривается после цикла).
for (k=0; k<=nm1-1; k++)
{
// Поиск главного элемента в текущем столбце (k):
for (i=k,amax=0.0; i<=nm1; i++)
if (fabs(a[i][k]) > fabs(amax)) amax=a[(imax=i)][k];
// Главный элемент найден.
// Если он =0, то ошибка, так как матрица вырождена и выход из функции
// (метка endofproc стоит в конце функции):
if (amax==0.0) { err=1; goto endofproc; }
// Замена строки с найденным главным элементом на строку с номером k
for (j=k;j<=nm1;j++)
{
t=a[imax][j];
a[imax][j]=a[k][j];
a[k][j]=t;
}
// Строки заменены.
// Замена элементов правой части для тех же строк:
t=b[imax];
b[imax]=b[k];
b[k]=t;
// Заменены.
// Определение mi для каждой строки (ниже главной)
// и ее преобразование для найденного mi:
for (i=k+1;i<=nm1;i++)
{
mi=-a[i][k]/amax;
a[i][k]=0.0;
for (j=k+1;j<=nm1;j++)
a[i][j]+=a[k][j]*mi;
|



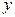 является функцией аргумента
является функцией аргумента  . Это означает, что любому значению
. Это означает, что любому значению  . В других случаях при известной зависимости
. В других случаях при известной зависимости  , в которой дискретному множеству значений аргумента
, в которой дискретному множеству значений аргумента 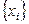 поставлено в соответствие множество значений функции
поставлено в соответствие множество значений функции 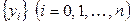 . Эти значения – либо результаты расчетов, либо экспериментальные данные. На практике могут понадобиться значения величины
. Эти значения – либо результаты расчетов, либо экспериментальные данные. На практике могут понадобиться значения величины 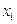 . Таким образом, приходим к необходимости использования имеющихся табличных данных для приближенного вычисления искомого параметра
. Таким образом, приходим к необходимости использования имеющихся табличных данных для приближенного вычисления искомого параметра  требуется аппроксимировать (приближенно заменить) некоторой функцией
требуется аппроксимировать (приближенно заменить) некоторой функцией  так, чтобы отклонение (в некотором смысле)
так, чтобы отклонение (в некотором смысле)  (1.1)
(1.1)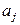 в процедурах подбираются так, чтобы достичь наименьшего отклонения многочлена от данной функции.
в процедурах подбираются так, чтобы достичь наименьшего отклонения многочлена от данной функции.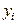 , что и функция
, что и функция  (1.2)
(1.2)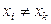 при
при 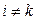 . Точки
. Точки 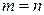 . В этом случае говорят о глобальной интерполяции, так как один многочлен
. В этом случае говорят о глобальной интерполяции, так как один многочлен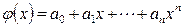 (1.3)
(1.3)
 и вектором свободных членов
и вектором свободных членов 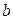 , методом Гаусса. Выполнение работы состоит из следующих этапов:
, методом Гаусса. Выполнение работы состоит из следующих этапов: , тип
, тип 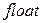 ;
;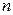 , тип
, тип 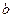 ), тип
), тип 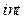 .
.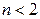 ;
;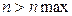 .
.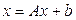 , (2.3)
, (2.3) - заданная числовая квадратная матрица n -го порядка, а b - заданный вектор (свободный член). Метод простой итерации состоит в следующем. Выбирается произвольный вектор x (начальное приближение), и строится итерационная последовательность векторов по формуле
- заданная числовая квадратная матрица n -го порядка, а b - заданный вектор (свободный член). Метод простой итерации состоит в следующем. Выбирается произвольный вектор x (начальное приближение), и строится итерационная последовательность векторов по формуле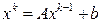 , (2.4)
, (2.4) , то система уравнений (2.3) имеет единственное решение
, то система уравнений (2.3) имеет единственное решение  и итерации (2.4) сходятся к решению со скоростью геометрической прогрессии [13]. Для оценки погрешности k -го приближения широко применяется неравенство
и итерации (2.4) сходятся к решению со скоростью геометрической прогрессии [13]. Для оценки погрешности k -го приближения широко применяется неравенство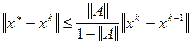 , (2.5)
, (2.5)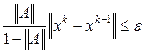 ,
,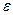 - некоторая заданная погрешность вычислений.
- некоторая заданная погрешность вычислений. - матрица коэффициентов преобразованной к виду (2.3) системы уравнений размера
- матрица коэффициентов преобразованной к виду (2.3) системы уравнений размера 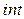 ;
; - количество знаков после запятой в мантиссе результата, остающихся после округления, тип
- количество знаков после запятой в мантиссе результата, остающихся после округления, тип 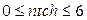 ;
;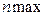 должна быть задана при разработке головной программы аналогично тому, как это делается при выполнении лабораторной работы № 11;
должна быть задана при разработке головной программы аналогично тому, как это делается при выполнении лабораторной работы № 11;


