
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интерполирование функций и Решение системСодержание книги Поиск на нашем сайте
ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
Методические указания к лабораторным работам по дисциплине “ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА”
Санкт-Петербург
УДК 519.7
Интерполирование функций и решение систем линейных алгебраических уравнений: Методические указания к лабораторным работам по дисциплине "Вычислительная математика" / Сост.: В.Н. Кафтасьев, А.Р. Лисс, М.С. Титов; СПбГЭТУ. СПб., 1998. 32 с.
Содержат формулировку заданий лабораторных работ и необходимые для их исполнения пояснения. При разработке лабораторных работ особое внимание уделяется вопросам исследования точности и обусловленности применяемых методов машинных вычислений. Предназначены для студентов ФАВТ направления "Информатика и вычислительная техника" и специальности 220400, а также для студентов других специальностей, изучающих численные методы решения задач на ЭВМ.
Утверждено редакционно-издательским советом университета в качестве методических указаний
© СПбГЭТУ, 1998
ВВЕДЕНИЕ
Цикл лабораторных работ предназначен для студентов 2-го курса (четвертый семестр), изучающих дисциплину “Вычислительная математика” и работающих в компьютерных классах на базе ЭВМ типа IBM PC AT-286 и выше, снабженных компилятором языка С (С++). Работы цикла посвящены отработке тем “Интерполирование функций” и “Задачи линейной алгебры”. Каждая из работ ставит целью изучение либо конкретного численного метода, либо набора численных процедур (схем, формул), позволяющих реализовать выполнение одной из классических задач вычислительной математики: интерполирование функций в случаях неравноотстоящих и равноотстоящих узлов и решение систем линейных алгебраических уравнений с использованием различных вычислительных способов. Порядок расположения лабораторных работ в методических указаниях соответствует последовательности изложения лекционного материала. Для углубленного изучения упомянутых задач и методов их решения целесообразно воспользоваться изданиями [1]-[10]. Данные методические указания являются продолжением материала, изложенного авторами в [11]. Выполнять каждую лабораторную работу следует поэтапно в следующем порядке: - подготовка к решению задачи на персональной ЭВМ (ПЭВМ);
- проведение вычислительного эксперимента на ПЭВМ; - анализ результатов вычислений; - оформление отчета. Подготовка к решению задачи на ПЭВМ производится как вне ком-пьютерного класса, так и непосредственно на ПЭВМ. Она включает: - ознакомление с описанием работы и заданием для выполнения; - составление программных модулей, содержащих определенные заданием и персональным вариантом вычислительные процедуры, и/или ввод исходных данных; - компиляцию разработанных программных модулей, их отладку и сопряжение с имеющимися для большинства работ программами-функциями, реализующими конкретные численные методы; - планирование вычислительного эксперимента на ПЭВМ в рамках выполняемого задания. Подпрограммы-функции, предназначенные для применения в процессе вычислений, представлены в виде библиотеки модулей на языке программирования С++. Это предопределяет ориентацию цикла работ на студентов, владеющих данным языком и навыками программирования в необходимом объеме. Проведение вычислительного эксперимента на ПЭВМ осуществляется в соответствии с порядком выполнения работы и заданием на исследование указанных зависимостей и обусловленности изучаемого метода. Анализ результатов вычислений заключается в построении исследуемых зависимостей и сравнительной оценке метода (вычислительной процедуры) по характерным для данной группы методов параметрам, например скорости сходимости, степени обусловленности, достижимой точности и т. п. Анализ результатов и оформление отчета производятся вне компьютерного класса. Отчет должен содержать: - постановку задачи; - тексты разработанных программ; - результаты вычислений, их теоретический и экспериментальный анализ в виде таблиц и графиков, снабженных необходимыми комментариями; - развернутые выводы по лабораторной работе.
ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ
Пусть величина
Наиболее распространенным и важным для практического использования случаем, когда вид связи между параметрами Этой цели служит задача о приближении (аппроксимации) функций: данную функцию Для практики важен случай аппроксимации функции многочленом
Этот случай, т. е. приближение многочленами, является одной из задач классического численного анализа [3], [4], [8], [10]. Рассмотрим аппроксимацию этого рода и методы ее реализации в вычислительных процедурах на ЭВМ. Коэффициенты Если приближение строится на заданном дискретном множестве точек
При данной постановке задачи предполагается, что среди значений Максимальная степень интерполяционного многочлена
используется для интерполяции функции Возможны два случая задания функции - точки - точки В каждом из указанных случаев для интерполирования функций применяются различные интерполяционные формулы. Их изучению посвящены, соответственно, лабораторные работы № 9 и № 10.
|
||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 311; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.220.148 (0.01 с.) |

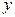 является функцией аргумента
является функцией аргумента  . Это означает, что любому значению
. Это означает, что любому значению  . В других случаях при известной зависимости
. В других случаях при известной зависимости  , в которой дискретному множеству значений аргумента
, в которой дискретному множеству значений аргумента 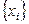 поставлено в соответствие множество значений функции
поставлено в соответствие множество значений функции 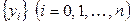 . Эти значения – либо результаты расчетов, либо экспериментальные данные. На практике могут понадобиться значения величины
. Эти значения – либо результаты расчетов, либо экспериментальные данные. На практике могут понадобиться значения величины 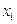 . Таким образом, приходим к необходимости использования имеющихся табличных данных для приближенного вычисления искомого параметра
. Таким образом, приходим к необходимости использования имеющихся табличных данных для приближенного вычисления искомого параметра  требуется аппроксимировать (приближенно заменить) некоторой функцией
требуется аппроксимировать (приближенно заменить) некоторой функцией  так, чтобы отклонение (в некотором смысле)
так, чтобы отклонение (в некотором смысле)  (1.1)
(1.1)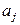 в процедурах подбираются так, чтобы достичь наименьшего отклонения многочлена от данной функции.
в процедурах подбираются так, чтобы достичь наименьшего отклонения многочлена от данной функции.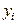 , что и функция
, что и функция  (1.2)
(1.2)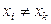 при
при 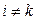 . Точки
. Точки 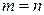 . В этом случае говорят о глобальной интерполяции, так как один многочлен
. В этом случае говорят о глобальной интерполяции, так как один многочлен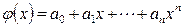 (1.3)
(1.3)



