
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценка погрешности формулы интерполяционного типаСодержание книги
Поиск на нашем сайте
Оценим погрешность формул интерполяционного типа. Априорная оценка погрешности интерполяции:
Отсюда погрешности вычисления интеграла:
Обозначив
(в предположении, что Квадратурная формула интерполяционного типа с
В частности, при
Если весовая функция отсутствует (
Справедливо также обратное утверждение: Если квадратурная формула
точна для любого многочлена степени n, то она является формулой интерполяционного типа. Для доказательства теоремы в качестве произвольного многочлена можем взять многочлен, входящий в состав интерполяционного многочлена Лагранжа:
поскольку с помощью линейной комбинации многочленов
По условию теоремы
Симметричные квадратурные формулы Рассмотрим квадратурную формулу
Пусть выполнены три условия. 1.
Обозначив
2. Узлы расположены симметрично относительно середины отрезка:
m – целая часть 3. Коэффициенты C – попарно равны:
Квадратурная формула называется симметричной, если выполнены все три условия: весовая функция четна, узлы расположены симметрично и коэффициенты попарно равны. Для симметричной квадратурной формулы интерполяционного типа третье свойство – попарное равенство коэффициентов – вытекает из первых двух. Докажем это.
Произведем замену переменной
Заменим теперь индекс суммирования
что и требовалось доказать. Наличие симметрии повышает точность квадратурных формул. Теорема. Симметричная квадратурная формула интерполяционного типа с нечетным числом узлов Доказательство. Произвольный многочлен степени
где
В последнем выражении два последних слагаемых являются многочленами степени n. Ранее уже было доказано, что квадратурная формула интерполяционного типа, построенная на
Вследствие нечетности функции
Следовательно, для доказательства теоремы нужно показать, что
Преобразуем
Обозначив в этом выражении суммы буквами
Таким образом,
Во второй строчке показано вычисление того же интеграла с помощью формулы Симпсона. Видим, что формула Симпсона дает точный результат. Формулы Ньютона-Котеса Формулами Ньютона-Котеса называются квадратурные формулы интерполяционного типа, построенные на равномерной сетке: Различают два типа формул Ньютона-Котеса: – замкнутого типа, когда – открытого типа, когда хотя бы один из узлов Рассмотрим формулы замкнутого типа: Преобразуем выражение для коэффициентов квадратурной формулы:
Произведем замену переменной интегрирования:
Учитывая, что
Если весовая функция
Если
Пример 12.9. Построим формулы Ньютона-Котеса с двумя и тремя узлами ( Если Если Ниже приведена таблица коэффициентов формул Ньютона-Котеса. Коэффициенты
Квадратурные формулы Гаусса
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 541; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.175.66 (0.008 с.) |



 , получим оценку погрешности квадратурной формулы интерполяционного типа:
, получим оценку погрешности квадратурной формулы интерполяционного типа:
 ). Отсюда следует утверждение:
). Отсюда следует утверждение: узлом:
узлом:  – точна для любого многочлена степени n. Т.е., если подынтегральная функция
– точна для любого многочлена степени n. Т.е., если подынтегральная функция 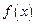 – многочлен степени n и коэффициенты
– многочлен степени n и коэффициенты  вычисляются по формуле (12.18), имеет место точное равенство:
вычисляются по формуле (12.18), имеет место точное равенство: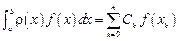 .
. имеем условие нормировки коэффициентов:
имеем условие нормировки коэффициентов: . (12.19)
. (12.19) ), то условие нормировки выглядит совсем просто:
), то условие нормировки выглядит совсем просто: . (12.20)
. (12.20) (12.21)
(12.21) ,
, можно описать любой многочлен степени n. Вычислим интегралы
можно описать любой многочлен степени n. Вычислим интегралы .
. . Поскольку
. Поскольку  , то
, то  . С другой стороны
. С другой стороны  . Таким образом,
. Таким образом, 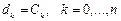 , что и требовалось доказать.
, что и требовалось доказать. . (12.22)
. (12.22) – функция, четная относительно середины отрезка
– функция, четная относительно середины отрезка 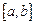 , т.е.
, т.е.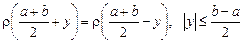 .
. , перепишем это равенство иначе
, перепишем это равенство иначе . (12.23)
. (12.23) , (12.24)
, (12.24) . Если количество узлов – нечетно (n – четно), то
. Если количество узлов – нечетно (n – четно), то  .
. . (12.25)
. (12.25) .
. :
: .
. :
: ,
, точна для любого многочлена степени
точна для любого многочлена степени 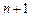 .
. ,
, – многочлен степени n. Используя формулу бинома Ньютона, запишем:
– многочлен степени n. Используя формулу бинома Ньютона, запишем: .
. .
. .
. .
. .
. , преобразуем вторую сумму. Заменим индекс суммирования:
, преобразуем вторую сумму. Заменим индекс суммирования: 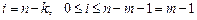 .
. (вследствие симметрии квадратурной формулы).
(вследствие симметрии квадратурной формулы). и
и  , что и требовалось доказать.
, что и требовалось доказать. Пример 12.8. Формула Симпсона, имеющая три узла, точна для любого многочлена третьей степени. На активной вставке рис. 12.5 в верхней строчке приведено аналитическое значение интеграла в симметричных пределах
Пример 12.8. Формула Симпсона, имеющая три узла, точна для любого многочлена третьей степени. На активной вставке рис. 12.5 в верхней строчке приведено аналитическое значение интеграла в симметричных пределах  от произвольного многочлена третьей степени
от произвольного многочлена третьей степени  . Знак “
. Знак “  ” означает в системе Mathcad применение символических преобразований. Коэффициенты a и c отсутствуют в решении, поскольку интегралы от нечетных функций в симметричных пределах равны нулю.
” означает в системе Mathcad применение символических преобразований. Коэффициенты a и c отсутствуют в решении, поскольку интегралы от нечетных функций в симметричных пределах равны нулю. .
. ;
; не совпадает с соответствующей граничной точкой отрезка
не совпадает с соответствующей граничной точкой отрезка  .
. .
.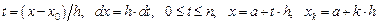 .
. .
. , получим
, получим . (12.26)
. (12.26) . Условие нормировки для коэффициентов B:
. Условие нормировки для коэффициентов B: . (12.27)
. (12.27)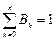 . (12.28)
. (12.28) ) и
) и  , получаем формулу трапеций:
, получаем формулу трапеций:  , и вследствие симметрии
, и вследствие симметрии  .
. , то
, то  . Учитывая условие нормировки и симметрию формулы, находим
. Учитывая условие нормировки и симметрию формулы, находим  . Получаем, тем самым, формулу Симпсона.
. Получаем, тем самым, формулу Симпсона. представлены в виде дробей
представлены в виде дробей  , где
, где  – общий знаменатель. В таблице представлены только коэффициенты формул с нечетным числом узлов. Все эти формулы имеют порядок
– общий знаменатель. В таблице представлены только коэффициенты формул с нечетным числом узлов. Все эти формулы имеют порядок  и дают точный результат для многочленов степени
и дают точный результат для многочленов степени 


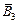






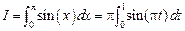 по формуле Ньютона-Котеса с пятью узлами. Точное значение интеграла равно
по формуле Ньютона-Котеса с пятью узлами. Точное значение интеграла равно  . Значения коэффициентов формулы берем из приведенной таблицы. Решение показано на рис. 12.6.
. Значения коэффициентов формулы берем из приведенной таблицы. Решение показано на рис. 12.6.


