
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Подынтегральная функция с бесконечными значениямиСодержание книги
Поиск на нашем сайте
Разобьем отрезок интегрирования на подотрезки так, чтобы особые точки находились только на концах подотрезка. 1. Аддитивное выделение особенности. Подынтегральная функция разбивается на сумму Пример 12.31. Пусть
Функция 2. Мультипликативное выделение особенности. Представим подынтегральную функцию в виде произведения Пример 12.32. Вычислим интеграл
Выделим весовую функцию
Задачи 1. Используя квадратурную формулу Гаусса с одним узлом и выбрав подходящую весовую функцию, вычислить интеграл:
2. Используя квадратурную формулу Гаусса с одним узлом и выбрав подходящую весовую функцию, вычислить интеграл:
3. Используя квадратурную формулу Гаусса с одним узлом и выбрав подходящую весовую функцию, вычислить интеграл:
4. Используя квадратурную формулу Гаусса с одним узлом и выбрав подходящую весовую функцию, вычислить интеграл:
5. Используя квадратурную формулу Гаусса с одним узлом и выбрав подходящую весовую функцию, вычислить интеграл:
6. Используя квадратурную формулу Гаусса с одним узлом и выбрав подходящую весовую функцию, вычислить интеграл:
7. Используя квадратурную формулу Гаусса с одним узлом и выбрав подходящую весовую функцию, вычислить интеграл:
8. Используя квадратурную формулу Гаусса с одним узлом и выбрав подходящую весовую функцию, вычислить интеграл:
9. Используя квадратурную формулу Гаусса с одним узлом и выбрав подходящую весовую функцию, вычислить интеграл:
10. Используя квадратурную формулу Гаусса с одним узлом и выбрав подходящую весовую функцию, вычислить интеграл:
11. Используя квадратурную формулу Гаусса с одним узлом и выбрав подходящую весовую функцию, вычислить интеграл:
12. Используя квадратурную формулу Гаусса с одним узлом и выбрав подходящую весовую функцию, вычислить интеграл:
13. Используя квадратурную формулу Гаусса с двумя узлами и выбрав подходящую весовую функцию, вычислить интеграл:
14. Используя квадратурную формулу Гаусса с двумя узлами и выбрав подходящую весовую функцию, вычислить интеграл:
15. Используя квадратурную формулу Гаусса с двумя узлами и выбрав подходящую весовую функцию, вычислить интеграл:
16. Используя квадратурную формулу Гаусса с двумя узлами и выбрав подходящую весовую функцию, вычислить интеграл:
17. Используя квадратурную формулу Гаусса с двумя узлами и выбрав подходящую весовую функцию, вычислить интеграл:
18. Используя квадратурную формулу Гаусса с двумя узлами и выбрав подходящую весовую функцию, вычислить интеграл:
19. Используя квадратурную формулу Гаусса с одним узлом и выбрав подходящую весовую функцию, вычислить интеграл:
20. Используя квадратурную формулу Гаусса с двумя узлами и выбрав подходящую весовую функцию, вычислить интеграл:
21. Используя квадратурную формулу Гаусса с двумя узлами и выбрав подходящую весовую функцию, вычислить интеграл:
22. Используя квадратурную формулу Гаусса с одним узлом и выбрав подходящую весовую функцию, вычислить интеграл:
Ответы
Обозначения:
H – значение интеграла, вычисленное по формуле Гаусса.
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22.
Вопросы для повторения
|
||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 248; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.42.22 (0.008 с.) |

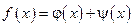 , где
, где  – ограниченная функция, а
– ограниченная функция, а 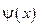 – функция, интегрируемая аналитическими методами.
– функция, интегрируемая аналитическими методами. , а интегрирование производится от точки
, а интегрирование производится от точки  . Тогда основная особенность имеет вид
. Тогда основная особенность имеет вид 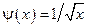 . Положим:
. Положим: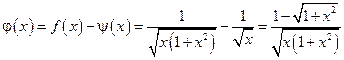 .
.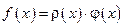 , где
, где 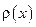 – положительна и интегрируема на отрезке
– положительна и интегрируема на отрезке  . Тогда можно рассматривать
. Тогда можно рассматривать 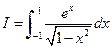 .
.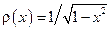 . Такой весовой функции соответствуют многочлены Чебышева. Квадратурная формула имеет вид:
. Такой весовой функции соответствуют многочлены Чебышева. Квадратурная формула имеет вид: , где
, где 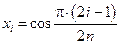 .
.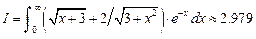

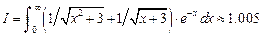

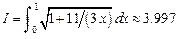

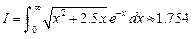

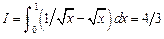



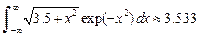


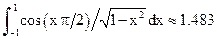




 .
.
 – весовая функция,
– весовая функция, – узлы и коэффициенты формулы Гаусса,
– узлы и коэффициенты формулы Гаусса, .
. .
.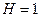 .
. .
. .
.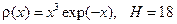 .
.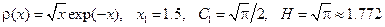 .
. .
. .
. .
.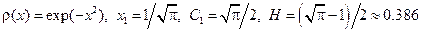 .
. .
. .
. .
. .
. .
. .
.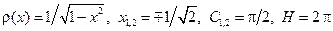 .
. .
.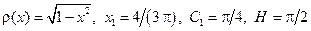 .
. , ортогональном с весом
, ортогональном с весом  любому многочлену степени меньше n.
любому многочлену степени меньше n.  ,
,  ,
,  ,
,  .
.


