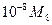Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Связь формул Гаусса с системами ортогональных многочленовСодержание книги
Поиск на нашем сайте
Из условия ортогональности (12.34) следует, что многочлены
Для многих весовых функций известны соответствующие ортогональные системы многочленов и формулы, позволяющие непосредственно вычислять положение узлов и коэффициенты формулы Гаусса.
1. r(x) º 1, a = -1, b = 1. Ортогональными многочленами с единичным весом на отрезке [-1,1] являются многочлены Лежандра:
Многочлены Лежандра удовлетворяют дифференциальному уравнению
Для решения уравнения достаточно задать только одно условие: Первые пять многочленов Лежандра показаны на рис. 12.13. Эти многочлены описываются формулами:
Многочлены Лежандра четной степени являются четными функциями; многочлены нечетной степени – нечетные функции. Ln(1)=1; Ln(-1)=1, если n – четное число, и Ln(-1)=-1, если n – нечетно. Для многочленов Лежандра существует рекуррентная формула:
Узлы и коэффициенты формулы Гаусса с n узлами связаны соотношением:
В пакете Mathematica встроенные многочлены Лежандра обозначаются LegendreP[n,x], в пакете Mathcad – Leg(n,x). На рис. 12.14 приведен пример расчета узлов и коэффициентов формулы Гаусса в среде Mathcad. Расчет проведен с использованием встроенных многочленов Лежандра. Корни многочлена вычисляются с помощью функции root(Leg(n,x), x). Для поиска корней предварительно в массиве y0,..,n задается неравномерная сетка n начальных значений корней, уточняемых в ходе вычислений. Вычисленные корни записываются как значения функции A(yk). Значения функции A(yk) используются для подсчета коэффициентов Ck. На рис. 12.14 показаны результаты подсчета для формулы с пятью узлами. Для контроля вычисляется сумма коэффициентов, которая должна быть равна интегралу от весовой функции:
Активизировав рисунок двойным щелчком мыши, можно провести расчет для другого количества узлов.
2.
Отметим, что многочленами Чебышева называют также многочлены Докажем ортогональность многочленов Чебышева. Для этого вычислим интеграл
После замены переменной:
Поскольку T0(x)=1, имеем также
Из формулы (12.43) легко определяются корни многочленов:
Для многочленов Чебышева справедливо рекуррентное соотношение
Первые пять многочленов Чебышева имеют вид:
Эти многочлены показаны на рис. 12.14. Все многочлены четной степени являются четными функциями, многочлены нечетной степени – нечетными. Максимальное отклонение от оси x на отрезке [-1,1] для многочленов Формулы Гаусса с данной весовой функцией называют также формулами Эрмита. Формула Эрмита имеет вид:
где узлы xk являются корнями многочлена Чебышева и все весовые коэффициенты одинаковы:
Докажем формулу (12.45), т.е. докажем, что эта формула точна для любого многочлена степени меньше 2n. Докажем вначале, что формула Эрмита точна для многочленов Чебышева степени m<2n:
Для многочлена нулевой степени точное значение интеграла равно
Такое же значение получаем по формуле Эрмита с n узлами:
В соответствии с формулой (12.44)
По формуле Эйлера можно записать
Во второй сумме заменим индекс суммирования:
Заменив в этой сумме индекс i на индекс k, объединим обе суммы:
По формуле суммы членов геометрической прогрессии найдем:
Таким образом, формула Эрмита точна для многочленов Чебышева степени m<2n, но поскольку любой многочлен степени <2n может быть представлен суммой многочленов Чебышева степени <2n, то формула Эрмита точна для произвольного многочлена степени <2n, что и требовалось доказать. В пакете Mathematica многочлены Чебышева первого рода обозначаются ChebyshevT[n,x], в пакете Mathcad – Tcheb(n,x). 3.
Узлы многочленов расположены в точках
Первые пять многочленов имеют вид:
Для многочленов Чебышева второго рода справедливо такое же рекуррентное соотношение, как и для многочленов первого рода
Для данной весовой функции условие нормировки коэффициентов формулы Гаусса имеет вид:
Многочлены второго рода в пакете Mathematica обозначаются ChebyshevU[n,x], в пакете Mathcad – Ucheb(n,x).
4.
Обозначения многочленов Чебышева-Эрмита: в пакете Mathematica –HermiteH[n,x], в пакете Mathcad – Her(n,x). Первые пять многочленов имеют вид:
Для многочленов Чебышева-Эрмита справедлива рекуррентная формула:
Многочлены удовлетворяют уравнению
Весовые коэффициенты могут быть вычислены по формулам:
Аналогичные расчеты легко провести в пакете Mathematica. Функция H[n_] дает список корней многочлена степени n: H[n_]:=Table[Roots[HermiteH[n,x]Š0,x][[k,2]], {k,n}] Для вычислений используется встроенная функция Roots. Функция CH[n_] дает список коэффициентов формулы Гаусса:
Коэффициенты вычисляются по формуле (12.35):
Для формулы с двумя узлами вычисленные значения узлов и коэффициентов равны
Для формулы с тремя узлами имеем:
Функция
Пример 12.24. Точное значение интеграла (12.47) для функции
5.
Если Первые три обобщенных многочлена имеют вид:
Для многочленов Лагерра справедливо рекуррентное соотношение
Производная обобщенного многочлена Лагерра равна
Весовые коэффициенты могут быть вычислены по формулам:
где В пакете Mathematica многочлены Лагерра обозначаются LaguerreL[n,x], обобщенные многочлены обозначаются LaguerreL[n,a,x]. В пакете Mathcad встроенными являются только простые многочлены Лагерра: Lag(n,x). Пример 12.25. С помощью средств пакета Mathematica построим формулу Гаусса для вычисления интегралов вида
Запустим программу Mathematica и введем функцию, дающую список узлов формулы Гаусса – список корней обобщенного многочлена Лагерра: L[n_,a_]:=Table[Roots[LaguerreL[n, a, x]==0, x][[k, 2]], {k, n}] Например, L[2, -1/2] дает список: С помощью второй из формул (12.48) найдем коэффициенты формулы Гаусса: LC[n_,a_]:=Table[Gamma[n] Gamma[a+n] L[n,a][[k]] / (((n-1)!)^2 n (a+n) (LaguerreL[n-1,a, L[n,a][[k]]])^2), {k,n}] В случае n=2, a=-1/2 эта команда выдает список: Используя введенные функции, запишем формулу Гаусса: HL[n_, a_, f_]:= Проверим построенную формулу на примере вычисления интеграла
Для этого интеграла значение, подсчитанное по формуле Гаусса c двумя узлами, совпадает с точным значением:
6. Ортогональными с весом
Первые два многочлена Якоби:
Если Многочлены Якоби удовлетворяют уравнению:
В пакете Mathematica встроенные многочлены Якоби обозначаются JacobiP[n,a,b,x], в пакете Mathcad – Jac(n,a,b,x). Пример 12.26. Используя средства пакета Mathematica, построим формулу Гаусса для вычисления интеграла
Узлы формулы Гаусса расположены в нулях многочлена Якоби. Введем функцию, для нахождения списка корней многочлена: JR[n_,a_,b_]:=Table[Roots[JacobiP[n,a,b,x]==0,x][[k,2]], {k,n}] (12.50) Например, Введем функцию для вычисления списка коэффициентов формулы Гаусса: JC[n_,a_,b_]:=Table[ ( Например, Запишем формулу Гаусса с n узлами для вычисления интеграла (12.49): HJ[n_,a_,b_,f_]:= Например, для интеграла Пример 12.27. Используя средства пакета Mathematica, построим формулу Гаусса для вычисления интеграла вида
После замены переменной x=(t+1)/2 получим
Для вычисления этого интеграла можно применить формулу Гаусса, узлы которой расположены в нулях многочлена J(n,0,-1/2,x). Воспользовавшись введенными выше функциями (12.50) и (12.51), запишем формулу Гаусса для вычисления интеграла (12.53): HJ0[n_, f_]:= Например, для интеграла вида (12.53), где
Процесс Эйткена
Для применения правила Рунге нужно знать порядок точности квадратурной формулы. Однако, реальный порядок формулы не всегда известен. Порядок формулы снижается, если подынтегральная формула имеет какие-либо особенности. Процесс Эйткена, использующий расчеты на трех сетках, позволяет уточнить результат и оценить реальный порядок квадратурной формулы. Пусть метод имеет неизвестный порядок p. Для упрощения расчетов выберем три сетки с постоянным отношением длины шагов:
Обозначим: I – точноезначение интеграла I k – значение интеграла, вычисленное на сетке с шагом h k. Ограничившись главным членом погрешности, можем записать оценки погрешности:
где С – постоянная. Имеем три уравнения и три неизвестных: I, C, p. Получаем
Отсюда
В правой части прибавим и вычтем слагаемое
Целесообразно использовать формулу для вычисления интеграла I использовать именно в таком виде: наиболее точное из трех вычислений Для оценки порядка квадратурной формулы попарно вычтем уравнения (3):
Отсюда находим эффективный порядок квадратурной формулы
Пример 12.28. Построим приближенные вычисления для интеграла
Результаты вычислений для разных значений шага сетки приведены в таблице.
Результаты вычислений далеки от точного значения интеграла. Применение процесса Эйткена совместно с формулой трапеций дает неплохой результат: 0.6680. Данная подынтегральная функция имеет особенность в точке В следующей таблице приведены оценки абсолютной величины погрешности для разных квадратурных формул на классе функций, имеющих на отрезке
Из таблицы видим, что реальный порядок квадратурной формулы не может быть больше порядка непрерывной производной подынтегральной функции.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 660; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.255.58 (0.009 с.) |

 , описывающие узлы формулы Гаусса с различным количеством узлов, образуют ортогональную систему:
, описывающие узлы формулы Гаусса с различным количеством узлов, образуют ортогональную систему: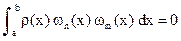 при
при  ,
, Рассмотрим примеры весовых функций.
Рассмотрим примеры весовых функций. .
. .
. .
.

 .
. .
.
 , a = -1, b = 1. Ортогональными многочленами с такой весовой функцией являются многочлены Чебышева первого рода
, a = -1, b = 1. Ортогональными многочленами с такой весовой функцией являются многочлены Чебышева первого рода . (12.43)
. (12.43) .
.
 .
. – получим
– получим
 при n>1. (12.44)
при n>1. (12.44) .
.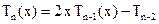 .
.

 равно 1.
равно 1. , (12.45)
, (12.45) .
.
 .
. .
. при 0<m<2n. Убедимся, что по формуле Эрмита также получим нулевое значение интеграла.
при 0<m<2n. Убедимся, что по формуле Эрмита также получим нулевое значение интеграла.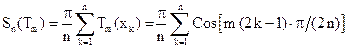 .
. .
. или
или  ; вторая сумма примет вид:
; вторая сумма примет вид: .
.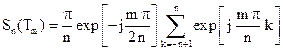 .
. .
.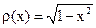 , a = -1, b = 1. Узлы квадратурной формулы Гаусса совпадают с корнями многочленов Чебышева второго рода:
, a = -1, b = 1. Узлы квадратурной формулы Гаусса совпадают с корнями многочленов Чебышева второго рода: .
. .
.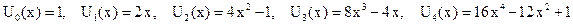 .
. .
. .
. , a = –¥, b = ¥. Семейство многочленов, ортогональных с данным весом на всей оси x, составляют многочлены Чебышева-Эрмита:
, a = –¥, b = ¥. Семейство многочленов, ортогональных с данным весом на всей оси x, составляют многочлены Чебышева-Эрмита: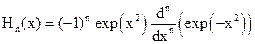 .
. .
. .
. .
. (12.46)
(12.46) На рис.12.16 показан расчет узлов и коэффициентов формулы Гаусса с весовой функцией
На рис.12.16 показан расчет узлов и коэффициентов формулы Гаусса с весовой функцией 
 .
. .
. .
. вычисляет по формуле Гаусса значение интеграла
вычисляет по формуле Гаусса значение интеграла . (12.47)
. (12.47) равно
равно  . Такое же значение дает формула Гаусса с двумя узлами
. Такое же значение дает формула Гаусса с двумя узлами  в полном согласии с тем фактом, что квадратурная формул с двумя уздами точна для многочлена третьей степени.
в полном согласии с тем фактом, что квадратурная формул с двумя уздами точна для многочлена третьей степени.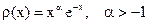 . Ортогональными многочленами с такой весовой функцией на положительной полуоси являются обобщенные многочлены Лагерра:
. Ортогональными многочленами с такой весовой функцией на положительной полуоси являются обобщенные многочлены Лагерра: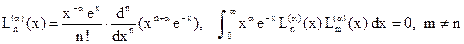 .
. , то многочлены называют просто многочленами Лагерра:
, то многочлены называют просто многочленами Лагерра: 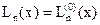 .
. .
. .
. .
. , (12.48)
, (12.48) – гамма-функция.
– гамма-функция. , где f(x) – непрерывная функция.
, где f(x) – непрерывная функция. .
.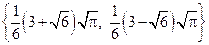 .
. LC[n, a][[k]] f[L[n, a][[k]] ]
LC[n, a][[k]] f[L[n, a][[k]] ]
 .
.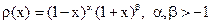 на отрезке [-1,1] являются многочлены Якоби:
на отрезке [-1,1] являются многочлены Якоби: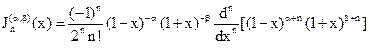 .
. .
. , многочлены Якоби пропорциональны многочленам Чебышева.
, многочлены Якоби пропорциональны многочленам Чебышева. .
. с весовой функцией
с весовой функцией  . (12.49)
. (12.49)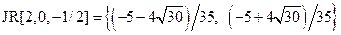 .
. (1-x)a (1+x)b
(1-x)a (1+x)b If[iŠk, 1, (x-JR[n,a,b][[i]]) / (JR[n,a,b][[k]]-JR[n,a,b][[i]])]) dx, {k,n} ] (12.51)
If[iŠk, 1, (x-JR[n,a,b][[i]]) / (JR[n,a,b][[k]]-JR[n,a,b][[i]])]) dx, {k,n} ] (12.51)
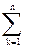 JC[n,a,b][[k]] f[JR[n,a,b][[k]]] (12.52)
JC[n,a,b][[k]] f[JR[n,a,b][[k]]] (12.52) , где
, где  формула (12.52) с тремя узлами HJ[3,-1/2,-1/2,f] дает точное значение
формула (12.52) с тремя узлами HJ[3,-1/2,-1/2,f] дает точное значение  .
. (12.53)
(12.53) .
. JC[n, 0, -1/2][[k]] f[(JR[n, 0, -1/2][[k]]+1) / 2]
JC[n, 0, -1/2][[k]] f[(JR[n, 0, -1/2][[k]]+1) / 2] , формула (12.52) с двумя узлами HJ0[2,f] дает точное значение 8/5.
, формула (12.52) с двумя узлами HJ0[2,f] дает точное значение 8/5.
 (12.54)
(12.54)

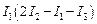 и найдем из полученного выражения I:
и найдем из полученного выражения I: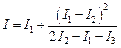 (12.55)
(12.55) плюс малая поправка.
плюс малая поправка.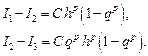

 (12.56)
(12.56)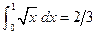 . Найдем значение интеграла по формуле трапеций и по формуле Симпсона. Для формулы трапеций будем использовать три сетки. Значения подынтегральной функции даны в таблице.
. Найдем значение интеграла по формуле трапеций и по формуле Симпсона. Для формулы трапеций будем использовать три сетки. Значения подынтегральной функции даны в таблице.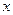

 – уже первая производная в этой точке обращается в бесконечность. Оценка с помощью процесса Эйткена порядка точности формулы трапеций для данной подынтегральной функции дает значение
– уже первая производная в этой точке обращается в бесконечность. Оценка с помощью процесса Эйткена порядка точности формулы трапеций для данной подынтегральной функции дает значение 
 кусочно непрерывную k -ю производную, ограниченную по модулю константой
кусочно непрерывную k -ю производную, ограниченную по модулю константой  . Стрелка в таблице означает перенос оценки из предыдущего столбца. таблица взята из книги: Калиткин Н.Н. “Численные методы”.
. Стрелка в таблице означает перенос оценки из предыдущего столбца. таблица взята из книги: Калиткин Н.Н. “Численные методы”.