
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Условия, обеспечивающие наивысшую точность квадратурной формулыСодержание книги
Поиск на нашем сайте
Рассмотрим теперь общий случай: квадратурная формула имеет произвольное число узлов m. Требуется найти расположение узлов
Корни многочлена совпадают с узлами квадратурной формулы. Теорема. О необходимых и достаточных условиях, обеспечивающих наивысшую алгебраическую степень точности квадратурной формулы. Квадратурная формула
точна для любого многочлена степени 1. многочлен
2. формула (12.33) является формулой интерполяционного типа, т.е. коэффициенты формулы определяются формулой:
Доказательство. Чтобы доказать необходимость, предположим, что формула (12.33) точна для любого многочлена степени Поскольку многочлен
Но, поскольку для любого значения Справедливость второго условия (12.35) следует из доказанной ранее теоремы: если квадратурная формула вида (12.33) точна для многочлена, степень которого на единицу меньше числа узлов, то эта формула является формулой интерполяционного типа. Тем самым доказана необходимость. Для доказательства достаточности предположим, что оба условия теоремы выполнены, и покажем, что в этом случае квадратурная формула (12.33) точна для любого многочлена степени Произвольный многочлен
где
Первый интеграл в этом выражении равен нулю в силу выполнения условия ортогональности, а второй в точности описывается квадратурной формулой интерполяционного типа; поэтому
Прибавим к правой части слагаемое
квадратурная формула (12.33) точна для произвольного многочлена Теорема полностью доказана. Следствия. 1. Условие ортогональности (12.34) эквивалентно требованиям:
Эти требования представляют собой систему уравнений относительно неизвестных · либо из n выбранных уравнений системы (12.30):
которая является линейной относительно коэффициентов Ck; · либо по формуле (12.35):
Во всех случаях целесообразно использовать условие нормировки (12.31):
Пример 12.17. Используя формулу Гаусса с одним узлом, вычислим интеграл:
Точное значение интеграла равно
Значение коэффициента найдем из условия нормировки:
Находим значение интеграла по формуле Гаусса: 2.
Пример 12.18. Как следует из примера 12.12, в случае единичной весовой функции и стандартного отрезка интегрирования 3. Рассмотрим множество многочленов
т.е. многочлены В частности, если весовая функция является четной относительно середины отрезка интегрирования, то нули многочленов
где
Таким образом, в случае четной весовой функции построение формулы Гаусса существенно упрощается. Произвольный отрезок интегрирования [a,b] можно привести к стандартному отрезку [-1,1] простым линейным преобразованием:
Здесь
Тогда
Не умаляя общности, можем далее рассматривать стандартный отрезок [-1,1]. Если весовая функция – четна, то узлы формулы Гаусса расположены симметрично, и многочлены
Пример 12. 19. Рассмотрим вновь случай
Отсюда находим Отметим, что уравнение Пример 12. 20. Пусть Уравнение для нахождения
Опять-таки отметим, что в данном примере уравнения
не позволяют найти значения Вообще, из уравнений вида Пример 12. 21. Построим формулу Гаусса с четырьмя узлами. Пусть Найдем вначале нули многочлена Для нахождения
Проинтегрировав, получим уравнения:
Умножив первое уравнение на 3 и вычтя его из второго, найдем:
Подставив значение
Решив это уравнение, получим:
Найдем теперь коэффициенты формулы Гаусса. Воспользуемся для этого системой уравнений (12.30).
Поскольку формула симметрична: при Решив эти уравнения, получим:
Пример 12. 22.
Построим формулу Гаусса с пятью узлами для стандартного отрезка интегрирования [-1,1], воспользовавшись вычислениями в среде Mathcad. Пусть весовая функция является четной; в частном случае 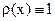 . Вычисления показаны на активной вставке – рис. 12.10. . Вычисления показаны на активной вставке – рис. 12.10.
Поскольку весовая функция – четна, то квадратурная формула – симметрична, и характеристический многочлен имеет вид Для нахождения коэффициентов квадратурной формулы так же, как и в предыдущем примере, воспользуемся системой уравнений (12.30), которую в данном случае запишем в виде
Выпишем матрицу системы M5 и столбец свободных коэффициентов V5. Затем используем встроенную функцию для решения систем линейных алгебраических уравнений lsolve. Вычисленные значения коэффициентов записываются как координаты вектора С5. Mathcad позволяет найти также и аналитическое решение, но аналитическое решение записывается довольно громоздко. После упрощения аналитическое решение для формулы с пятью узлами
Формулы, приведенные на рис. 12.10, справедливы для произвольной четной весовой функции. “Оживив” рисунок и введя новую весовую функцию
Пример 12. 23. Вычислим интеграл Выделим весовую функцию: Найдем коэффициенты формулы Ньютона-Котеса. Обозначим x1=0, x2=1. Согласно формуле (12.35) получим
Положение узла x1 формулы Гаусса находим из условия ортогональности (12.37):
Вычислив интеграл, получим
Расчеты, проведенные в среде Mathcad, показаны на рис. 12.11. Видим, что погрешность расчетов по формуле Гаусса с одним узлом примерно в полтора раза меньше погрешности расчетов по формуле Ньютона-Котеса с двумя узлами. Расчеты в среде Mathcad для формулы Гаусса с двумя узлами приведены на рис. 12.12. Уравнения для нахождения узлов записываются между двумя служебными словами Given и Find. Для решения системы уравнений методом последовательных приближений предварительно задаются начальные значения узлов x1, x2. Вычисленные значения узлов записываются в векторе XH2. Коэффициенты рассчитываются по формуле (12.37); результаты вычислений записываются в векторе С. Видим, что погрешность вычислений данного интеграла по формуле Гаусса на 5 порядков меньше погрешности формулы Ньютона-Котеса с тем же количеством узлов.
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 394; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.91.173 (0.006 с.) |

 и значения весовых коэффициентов
и значения весовых коэффициентов  . Введем в рассмотрение многочлен, описывающий узлы квадратурной формулы:
. Введем в рассмотрение многочлен, описывающий узлы квадратурной формулы: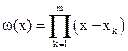 .
. – (12.33)
– (12.33) тогда и только тогда, когда выполнены два условия:
тогда и только тогда, когда выполнены два условия: на отрезке [a,b] ортогонален с весом
на отрезке [a,b] ортогонален с весом  любому многочлену
любому многочлену  степени меньше m, т.е.
степени меньше m, т.е. ; (12.34)
; (12.34) , где
, где  (12.35)
(12.35) и покажем, что в этом случае выполняются оба условия теоремы.
и покажем, что в этом случае выполняются оба условия теоремы. , имеет степень
, имеет степень  , то в силу сделанного предположения справедливо равенство
, то в силу сделанного предположения справедливо равенство .
. , обе части этого выражения равны нулю. Отсюда следует свойство ортогональности (12.34).
, обе части этого выражения равны нулю. Отсюда следует свойство ортогональности (12.34). степени
степени  , (12.36)
, (12.36) и
и  – многочлены, степени не выше
– многочлены, степени не выше  :
:  .
. .
. , равное нулю, и объединим две суммы в одну, учитывая равенство (12.36). Получим в итоге
, равное нулю, и объединим две суммы в одну, учитывая равенство (12.36). Получим в итоге –
– .
. (12.37)
(12.37) . Таким образом, получаем более простую систему уравнений для нахождения узлов формулы Гаусса. После того, как узлы найдены, коэффициенты формулы
. Таким образом, получаем более простую систему уравнений для нахождения узлов формулы Гаусса. После того, как узлы найдены, коэффициенты формулы 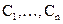 могут быть найдены
могут быть найдены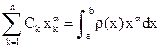 ,
, .
.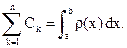
 .
. . В качестве весовой функции выберем функцию
. В качестве весовой функции выберем функцию  , описывающую убывание подынтегральной функции при
, описывающую убывание подынтегральной функции при  . Из условия ортогональности определяем расположение узла формулы Гаусса:
. Из условия ортогональности определяем расположение узла формулы Гаусса: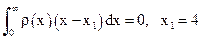 .
. .
. . Относительная погрешность вычислений составляет примерно 3%.
. Относительная погрешность вычислений составляет примерно 3%. Из уравнений (12.37) при
Из уравнений (12.37) при  получаем свойство многочлена
получаем свойство многочлена  . (12.38)
. (12.38) многочлен, описывающий узлы квадратурной формулы равен
многочлен, описывающий узлы квадратурной формулы равен  . Кривая
. Кривая 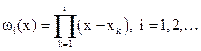 , описывающих узлы квадратурной формулы. Из доказанной теоремы следует, что
, описывающих узлы квадратурной формулы. Из доказанной теоремы следует, что при
при  , (12.39)
, (12.39) образуют систему многочленов, ортогональных с весом
образуют систему многочленов, ортогональных с весом  расположены симметрично:
расположены симметрично: ,
,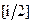 обозначает целую часть числа
обозначает целую часть числа  . Из теоремы о симметричных квадратурных формулах интерполяционного типа следует, что коэффициенты формулы Гаусса в этом случае попарно равны:
. Из теоремы о симметричных квадратурных формулах интерполяционного типа следует, что коэффициенты формулы Гаусса в этом случае попарно равны: .
.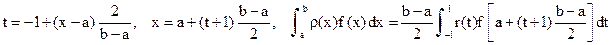 .
.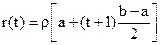 – весовая функция в новых координатах. При линейном преобразовании четность весовой функции сохраняется. Сохранение четности весовой функции объясняется тем, что при линейном преобразовании все части отрезка растягиваются или сжимаются равномерно. Действительно, пусть весовая функция
– весовая функция в новых координатах. При линейном преобразовании четность весовой функции сохраняется. Сохранение четности весовой функции объясняется тем, что при линейном преобразовании все части отрезка растягиваются или сжимаются равномерно. Действительно, пусть весовая функция  , или
, или  .
.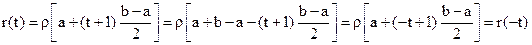 .
. четной степени являются четными функциями, а многочлены
четной степени являются четными функциями, а многочлены  нечетной степени – нечетными функциями, т.е.
нечетной степени – нечетными функциями, т.е. .
. . Найдем теперь расположение узлов формулы Гаусса, используя свойства ортогональности и симметрии:
. Найдем теперь расположение узлов формулы Гаусса, используя свойства ортогональности и симметрии: или
или 
 .
.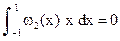 не позволяет найти значение
не позволяет найти значение  , т.к. интеграл от нечетной функции
, т.к. интеграл от нечетной функции  всегда равен нулю независимо от значения
всегда равен нулю независимо от значения  . Найдем многочлен
. Найдем многочлен  .
. , т.е.
, т.е. .
. и
и 
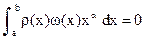 для вычисления узлов
для вычисления узлов  .
.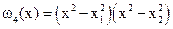 .
. достаточно взять два уравнения вида
достаточно взять два уравнения вида .
.
 .
. .
.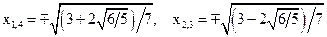 .
.
 – достаточно выписать лишь два уравнения:
– достаточно выписать лишь два уравнения: и при
и при  .
. .
.
 . Соответственно, система уравнений для нахождения узлов включает только два уравнения. Как обычно, используем условия ортогональности (12.37). Множители
. Соответственно, система уравнений для нахождения узлов включает только два уравнения. Как обычно, используем условия ортогональности (12.37). Множители 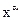 в подынтегральном выражении выбираем так, чтобы подынтегральная функция была четной. Система уравнений в среде Mathcad записывается между служебными словами Given и Find. Предварительно задаются начальные значения x1, x2 для поиска решения методом последовательных приближений. Вычисленные значения узлов записываются как координаты вектора X5.
в подынтегральном выражении выбираем так, чтобы подынтегральная функция была четной. Система уравнений в среде Mathcad записывается между служебными словами Given и Find. Предварительно задаются начальные значения x1, x2 для поиска решения методом последовательных приближений. Вычисленные значения узлов записываются как координаты вектора X5. ,
, можно записать в виде
можно записать в виде

 , получим ответ:
, получим ответ: .
.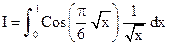 с помощью формулы Ньютона-Котеса с двумя узлами, а также с помощью формул Гаусса с одним и двумя узлами. Данный интеграл легко вычисляется аналитически (
с помощью формулы Ньютона-Котеса с двумя узлами, а также с помощью формул Гаусса с одним и двумя узлами. Данный интеграл легко вычисляется аналитически (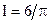 ), что позволяет сравнить приближенные решения с точным.
), что позволяет сравнить приближенные решения с точным. . В соответствии с условием нормировки коэффициентов квадратурной формулы
. В соответствии с условием нормировки коэффициентов квадратурной формулы  .
. , и по условию нормировки C1=2-C2=4/3.
, и по условию нормировки C1=2-C2=4/3. .
. , отсюда x1=1/3. Значение коэффициента С1 формулы Гаусса по условию нормировки равно 2.
, отсюда x1=1/3. Значение коэффициента С1 формулы Гаусса по условию нормировки равно 2.




