
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Квадратурная формула СимпсонаСодержание книги
Поиск на нашем сайте
Численное интегрирование
Содержание 12.1. Простейшие квадратурные формулы.. 2 12.2. Квадратурная формула Симпсона.. 4 12.3. Правило Рунге. 4 12.4. Формула сплайн-квадратуры.. 5 12.5. Адаптивные квадратурные алгоритмы.. 6 12.6. Квадратурные формулы интерполяционного типа.. 7 12.6.1. Определение формулы интерполяционного типа. 7 12.6.2. Оценка погрешности формулы интерполяционного типа. 8 12.6.3. Симметричные квадратурные формулы.. 9 12.7. Формулы Ньютона-Котеса.. 10 12.8. Квадратурные формулы Гаусса.. 11 12.8.1. Квадратурные формулы наивысшей алгебраической степени точности. 11 12.8.2. Условия, обеспечивающие наивысшую точность квадратурной формулы.. 15 12.8.3. Теоремы о многочлене, определяющем положение узлов формулы Гаусса. 21 12.8.4. Свойство коэффициентов формулы Гаусса. 22 12.8.5. Оценка погрешности формул Гаусса. 22 12.8.6. Связь формул Гаусса с системами ортогональных многочленов. 22 12.9. Процесс Эйткена.. 28 12.10. Интегрирование разрывных функций.. 29 12.11. Вычисление интегралов с переменным пределом интегрирования.. 30 12.12. Вычисление несобственных интегралов.. 30 12.12.1. Интегралы с бесконечными пределами. 30 12.12.2. Подынтегральная функция с бесконечными значениями. 31 Задачи.. 32 Ответы.. 34 Вопросы для повторения.. 34
Формулы для приближенного вычисления определенных интегралов называют квадратурными формулами. Пусть речь идет о вычислении интеграла
Предполагаем, что функция f (x) определена и может быть вычислена для любого Пусть отрезок интегрирования [ a,b ] разбит на n подотрезков
Простой квадратурной формулой называется каждая формула, аппроксимирующая отдельный интеграл Составная квадратурная формула – это формула, дающая представление интеграла в виде суммы (12.2). Две простейшие квадратурные формулы: формула прямоугольников и формула трапеций. Обозначим:
Формула прямоугольников аппроксимирует каждый интеграл
Составная формула прямоугольников:
Формула трапеций аппроксимирует каждый интеграл
Составная формула трапеций:
Обозначим Предположим, что функция
Найдем интеграл
Проинтегрируем ряд (12.6)
Из этой формулы следует, что при малых Найдем погрешность формулы трапеций. Подставим в формулу (12.6) значения
Умножим (12.8) на
Получаем отсюда
Таким образом, при малых Общая погрешность каждой из формул равна сумме погрешностей на отдельных подотрезках. Введем обозначения:
Тогда
Если все Формулы прямоугольников и трапеций имеют второй порядок точности, они дают точное значение интеграла для линейной подынтегральной функции.
Пример 12.1. С помощью формул прямоугольников и трапеций вычислим интеграл
Правило Рунге Если подынтегральная функция – достаточно гладкая, то правило Рунге позволяет найти оценку погрешности приближенного интегрирования. Пусть вычисления проводятся с помощью квадратурной формулы, имеющей порядок p. Обозначим:
Погрешность вычислений:
где C – константа, зависящая от значения производной
Первая формула Рунге – оценка погрешности вычислений с делением отрезка пополам:
Вторая формула Рунге – уточненный результат:
Замечание. Формулы Рунге применимы, когда известен порядок точности квадратурной формулы. Однако, порядок формулы зависит от гладкости подынтегральной функции. Для функций, имеющих особенности, порядок точности уменьшается и формулы Рунге неприменимы.
Пример 12.3. С помощью составной формулы трапеций вычислим интеграл от гладкой функции  на отрезке на отрезке  , поделив отрезок на , поделив отрезок на  подотрезков. Повторим вычисления для удвоенного числа отрезков и уточним результат по правилу Рунге. На рис.12.3 приведено решение в среде Mathcad. подотрезков. Повторим вычисления для удвоенного числа отрезков и уточним результат по правилу Рунге. На рис.12.3 приведено решение в среде Mathcad.
Пример 12.4. Используя формулу трапеций и правило Рунге, найдем более точную квдратурную формулу. Обозначим:
Формула трапеций на всем отрезке Формула трапеций при делении отрезка Уточненное значение интеграла:
Получили формулу Симпсона.
Формула сплайн-квадратуры Кубический сплайн на отрезке
где Заметим, что
Следовательно,
Формула сплайн-квадратуры есть формула трапеций плюс поправочный член, зависящий от коэффициентов
Таким образом, поправочный член аппроксимирует главный член погрешности формулы трапеций. Пример 12.5. Вычислим интеграл
Расстояние между узлами равно
Для естественного сплайна
Сравнивая точность вычислений интеграла
Формулы Ньютона-Котеса Формулами Ньютона-Котеса называются квадратурные формулы интерполяционного типа, построенные на равномерной сетке: Различают два типа формул Ньютона-Котеса: – замкнутого типа, когда – открытого типа, когда хотя бы один из узлов Рассмотрим формулы замкнутого типа: Преобразуем выражение для коэффициентов квадратурной формулы:
Произведем замену переменной интегрирования:
Учитывая, что
Если весовая функция
Если
Пример 12.9. Построим формулы Ньютона-Котеса с двумя и тремя узлами ( Если Если Ниже приведена таблица коэффициентов формул Ньютона-Котеса. Коэффициенты
Квадратурные формулы Гаусса Процесс Эйткена
Для применения правила Рунге нужно знать порядок точности квадратурной формулы. Однако, реальный порядок формулы не всегда известен. Порядок формулы снижается, если подынтегральная формула имеет какие-либо особенности. Процесс Эйткена, использующий расчеты на трех сетках, позволяет уточнить результат и оценить реальный порядок квадратурной формулы. Пусть метод имеет неизвестный порядок p. Для упрощения расчетов выберем три сетки с постоянным отношением длины шагов:
Обозначим: I – точноезначение интеграла I k – значение интеграла, вычисленное на сетке с шагом h k. Ограничившись главным членом погрешности, можем записать оценки погрешности:
где С – постоянная. Имеем три уравнения и три неизвестных: I, C, p. Получаем
Отсюда
В правой части прибавим и вычтем слагаемое
Целесообразно использовать формулу для вычисления интеграла I использовать именно в таком виде: наиболее точное из трех вычислений Для оценки порядка квадратурной формулы попарно вычтем уравнения (3):
Отсюда находим эффективный порядок квадратурной формулы
Пример 12.28. Построим приближенные вычисления для интеграла
Результаты вычислений для разных значений шага сетки приведены в таблице.
Результаты вычислений далеки от точного значения интеграла. Применение процесса Эйткена совместно с формулой трапеций дает неплохой результат: 0.6680. Данная подынтегральная функция имеет особенность в точке В следующей таблице приведены оценки абсолютной величины погрешности для разных квадратурных формул на классе функций, имеющих на отрезке
Из таблицы видим, что реальный порядок квадратурной формулы не может быть больше порядка непрерывной производной подынтегральной функции.
Задачи 1. Используя квадратурную формулу Гаусса с одним узлом и выбрав подходящую весовую функцию, вычислить интеграл:
2. Используя квадратурную формулу Гаусса с одним узлом и выбрав подходящую весовую функцию, вычислить интеграл:
3. Используя квадратурную формулу Гаусса с одним узлом и выбрав подходящую весовую функцию, вычислить интеграл:
4. Используя квадратурную формулу Гаусса с одним узлом и выбрав подходящую весовую функцию, вычислить интеграл:
5. Используя квадратурную формулу Гаусса с одним узлом и выбрав подходящую весовую функцию, вычислить интеграл:
6. Используя квадратурную формулу Гаусса с одним узлом и выбрав подходящую весовую функцию, вычислить интеграл:
7. Используя квадратурную формулу Гаусса с одним узлом и выбрав подходящую весовую функцию, вычислить интеграл:
8. Используя квадратурную формулу Гаусса с одним узлом и выбрав подходящую весовую функцию, вычислить интеграл:
9. Используя квадратурную формулу Гаусса с одним узлом и выбрав подходящую весовую функцию, вычислить интеграл:
10. Используя квадратурную формулу Гаусса с одним узлом и выбрав подходящую весовую функцию, вычислить интеграл:
11. Используя квадратурную формулу Гаусса с одним узлом и выбрав подходящую весовую функцию, вычислить интеграл:
12. Используя квадратурную формулу Гаусса с одним узлом и выбрав подходящую весовую функцию, вычислить интеграл:
13. Используя квадратурную формулу Гаусса с двумя узлами и выбрав подходящую весовую функцию, вычислить интеграл:
14. Используя квадратурную формулу Гаусса с двумя узлами и выбрав подходящую весовую функцию, вычислить интеграл:
15. Используя квадратурную формулу Гаусса с двумя узлами и выбрав подходящую весовую функцию, вычислить интеграл:
16. Используя квадратурную формулу Гаусса с двумя узлами и выбрав подходящую весовую функцию, вычислить интеграл:
17. Используя квадратурную формулу Гаусса с двумя узлами и выбрав подходящую весовую функцию, вычислить интеграл:
18. Используя квадратурную формулу Гаусса с двумя узлами и выбрав подходящую весовую функцию, вычислить интеграл:
19. Используя квадратурную формулу Гаусса с одним узлом и выбрав подходящую весовую функцию, вычислить интеграл:
20. Используя квадратурную формулу Гаусса с двумя узлами и выбрав подходящую весовую функцию, вычислить интеграл:
21. Используя квадратурную формулу Гаусса с двумя узлами и выбрав подходящую весовую функцию, вычислить интеграл:
22. Используя квадратурную формулу Гаусса с одним узлом и выбрав подходящую весовую функцию, вычислить интеграл:
Ответы
Обозначения:
H – значение интеграла, вычисленное по формуле Гаусса.
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22.
Вопросы для повторения
Численное интегрирование
Содержание 12.1. Простейшие квадратурные формулы.. 2 12.2. Квадратурная формула Симпсона.. 4 12.3. Правило Рунге. 4 12.4. Формула сплайн-квадратуры.. 5 12.5. Адаптивные квадратурные алгоритмы.. 6 12.6. Квадратурные формулы интерполяционного типа.. 7 12.6.1. Определение формулы интерполяционного типа. 7 12.6.2. Оценка погрешности формулы интерполяционного типа. 8 12.6.3. Симметричные квадратурные формулы.. 9 12.7. Формулы Ньютона-Котеса.. 10 12.8. Квадратурные формулы Гаусса.. 11 12.8.1. Квадратурные формулы наивысшей алгебраической степени точности. 11 12.8.2. Условия, обеспечивающие наивысшую точность квадратурной формулы.. 15 12.8.3. Теоремы о многочлене, определяющем положение узлов формулы Гаусса. 21 12.8.4. Свойство коэффициентов формулы Гаусса. 22 12.8.5. Оценка погрешности формул Гаусса. 22 12.8.6. Связь формул Гаусса с системами ортогональных многочленов. 22 12.9. Процесс Эйткена.. 28 12.10. Интегрирование разрывных функций.. 29 12.11. Вычисление интегралов с переменным пределом интегрирования.. 30 12.12. Вычисление несобственных интегралов.. 30 12.12.1. Интегралы с бесконечными пределами. 30 12.12.2. Подынтегральная функция с бесконечными значениями. 31 Задачи.. 32 Ответы.. 34 Вопросы для повторения.. 34
Формулы для приближенного вычисления определенных интегралов называют квадратурными формулами. Пусть речь идет о вычислении интеграла
Предполагаем, что функция f (x) определена и может быть вычислена для любого Пусть отрезок интегрирования [ a,b ] разбит на n подотрезков
Простой квадратурной формулой называется каждая формула, аппроксимирующая отдельный интеграл Составная квадратурная формула – это формула, дающая представление интеграла в виде суммы (12.2). Две простейшие квадратурные формулы: формула прямоугольников и формула трапеций. Обозначим:
Формула прямоугольников аппроксимирует каждый интеграл
Составная формула прямоугольников:
Формула трапеций аппроксимирует каждый интеграл
Составная формула трапеций:
Обозначим Предположим, что функция
Найдем интеграл
Проинтегрируем ряд (12.6)
Из этой формулы следует, что при малых Найдем погрешность формулы трапеций. Подставим в формулу (12.6) значения
Умножим (12.8) на
Получаем отсюда
Таким образом, при малых Общая погрешность каждой из формул равна сумме погрешностей на отдельных подотрезках. Введем обозначения:
Тогда
Если все Формулы прямоугольников и трапеций имеют второй порядок точности, они дают точное значение интеграла для линейной подынтегральной функции.
Пример 12.1. С помощью формул прямоугольников и трапеций вычислим интеграл
Квадратурная формула Симпсона
В соответствии с формулами (12.9), (12.10) предыдущего раздела погрешности формул прямоуг
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 1417; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.7.116 (0.01 с.) |

 (12.1)
(12.1) .
. . Пусть, далее,
. Пусть, далее,  . Ясно, интеграл
. Ясно, интеграл  можно представить в виде суммы
можно представить в виде суммы , где
, где  . (12.2)
. (12.2) .
. . (12.3)
. (12.3) и высотой
и высотой  :
: .
. . (12.4)
. (12.4)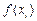 до
до  :
: .
. . (12.5)
. (12.5) . Если
. Если  интегрируема по Риману, то
интегрируема по Риману, то  .
. :
: (12.6)
(12.6)
 (12.7)
(12.7) плюс члены более высокого порядка.
плюс члены более высокого порядка. и
и 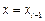 :
: ,
, ,
,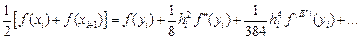 . (12.8)
. (12.8)

 плюс члены более высокого порядка.
плюс члены более высокого порядка. . (12.9)
. (12.9)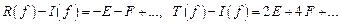
 (12.10)
(12.10)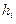 достаточно малы и производная
достаточно малы и производная  не слишком велика,
не слишком велика,  , и главный член погрешности зависит от
, и главный член погрешности зависит от  . Отсюда следует, в частности, что для многих функций формула прямоугольников примерно в два раза точнее формулы трапеций.
. Отсюда следует, в частности, что для многих функций формула прямоугольников примерно в два раза точнее формулы трапеций.
 , разбив отрезок интегрирования на два подотрезка. Сравним полученные результаты с точным значением интеграла
, разбив отрезок интегрирования на два подотрезка. Сравним полученные результаты с точным значением интеграла  . Решение в среде Mathcad показано на рис. 12.1. Видим, что погрешность формулы трапеций примерно в 2 раза выше погрешности формулы прямоугольников.
. Решение в среде Mathcad показано на рис. 12.1. Видим, что погрешность формулы трапеций примерно в 2 раза выше погрешности формулы прямоугольников. – результат приближенного вычисления интеграла
– результат приближенного вычисления интеграла  – результат приближенного вычисления того же интеграла при делении отрезка
– результат приближенного вычисления того же интеграла при делении отрезка  .
. ,
, ,
,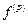 .
. .
. (12.13)
(12.13) (12.14)
(12.14)
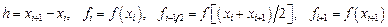
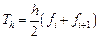
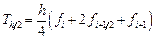

 , (12.15)
, (12.15)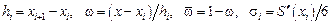 .
. ,
,  .
. . (12.16)
. (12.16) . Оценим значение этой поправки, предполагая, что функция
. Оценим значение этой поправки, предполагая, что функция 
 .
. . Находим
. Находим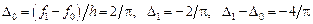 .
. и уравнение для нахождения
и уравнение для нахождения  имеет вид:
имеет вид: 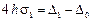 . Отсюда
. Отсюда  . Учитывая, что значения интегралов на двух подотрезках одинаковы, получаем по формуле сплайн-квадратуры
. Учитывая, что значения интегралов на двух подотрезках одинаковы, получаем по формуле сплайн-квадратуры .
. .
. ;
; не совпадает с соответствующей граничной точкой отрезка
не совпадает с соответствующей граничной точкой отрезка 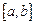 .
. .
. .
.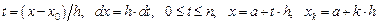 .
. .
. , получим
, получим . (12.26)
. (12.26) – четна, то формулы Ньютона-Котеса – симметричны
– четна, то формулы Ньютона-Котеса – симметричны  . Условие нормировки для коэффициентов B:
. Условие нормировки для коэффициентов B: . (12.27)
. (12.27) , то
, то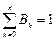 . (12.28)
. (12.28) ) и
) и  , получаем формулу трапеций:
, получаем формулу трапеций:  , и вследствие симметрии
, и вследствие симметрии  .
. , то
, то  . Учитывая условие нормировки и симметрию формулы, находим
. Учитывая условие нормировки и симметрию формулы, находим  . Получаем, тем самым, формулу Симпсона.
. Получаем, тем самым, формулу Симпсона. представлены в виде дробей
представлены в виде дробей  , где
, где  – общий знаменатель. В таблице представлены только коэффициенты формул с нечетным числом узлов. Все эти формулы имеют порядок
– общий знаменатель. В таблице представлены только коэффициенты формул с нечетным числом узлов. Все эти формулы имеют порядок  и дают точный результат для многочленов степени
и дают точный результат для многочленов степени 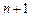 .
.


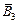






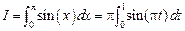 по формуле Ньютона-Котеса с пятью узлами. Точное значение интеграла равно
по формуле Ньютона-Котеса с пятью узлами. Точное значение интеграла равно 
 (12.54)
(12.54)

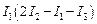 и найдем из полученного выражения I:
и найдем из полученного выражения I: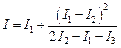 (12.55)
(12.55) плюс малая поправка.
плюс малая поправка.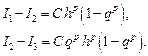

 (12.56)
(12.56)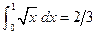 . Найдем значение интеграла по формуле трапеций и по формуле Симпсона. Для формулы трапеций будем использовать три сетки. Значения подынтегральной функции даны в таблице.
. Найдем значение интеграла по формуле трапеций и по формуле Симпсона. Для формулы трапеций будем использовать три сетки. Значения подынтегральной функции даны в таблице.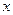

 – уже первая производная в этой точке обращается в бесконечность. Оценка с помощью процесса Эйткена порядка точности формулы трапеций для данной подынтегральной функции дает значение
– уже первая производная в этой точке обращается в бесконечность. Оценка с помощью процесса Эйткена порядка точности формулы трапеций для данной подынтегральной функции дает значение 
 кусочно непрерывную k -ю производную, ограниченную по модулю константой
кусочно непрерывную k -ю производную, ограниченную по модулю константой  . Стрелка в таблице означает перенос оценки из предыдущего столбца. таблица взята из книги: Калиткин Н.Н. “Численные методы”.
. Стрелка в таблице означает перенос оценки из предыдущего столбца. таблица взята из книги: Калиткин Н.Н. “Численные методы”.

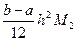











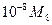
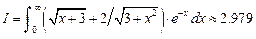

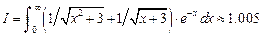

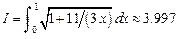

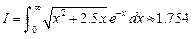

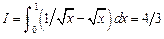



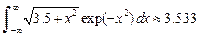


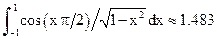




 .
.
 – весовая функция,
– весовая функция, – узлы и коэффициенты формулы Гаусса,
– узлы и коэффициенты формулы Гаусса, .
. .
.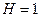 .
. .
. .
.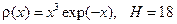 .
.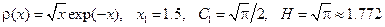 .
. .
. .
. .
.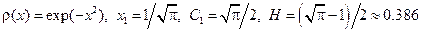 .
. .
. .
. .
. .
. .
. .
.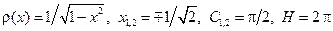 .
. .
.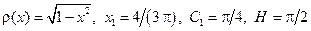 .
. , ортогональном с весом
, ортогональном с весом  любому многочлену степени меньше n.
любому многочлену степени меньше n.  ,
,  ,
,  ,
,  .
.


