
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Адаптивные квадратурные алгоритмыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В адаптивных квадратурных программах отрезок интегрирования
В соответствии с правилом Рунге оценка погрешности вычислений на отрезке
где
p – порядок точности квадратурной формулы. Основная операция типичной адаптивной программы состоит в делении каждого подотрезка пополам до тех пор, пока не будет выполнено следующее условие
где Отметим, что приведенные рассуждения справедливы, если подынтегральная функция имеет p непрерывных производных, и, соответственно, погрешность на каждом подотрезке пропорциональна величине В системе Help системы Mathcad приведен пример простой адаптивной программы, в которой отрезок интегрирования делится на отрезки равной длины. Программа показана на рис. 12.4. Программа состоит из двух подпрограмм: Simpson(f,a,b,N) и Adapt(f,a,b). Первая подпрограмма вычисляет интеграл по формуле Симпсона на отрезке [a,b] для подынтегральной функции f; при этом отрезок [a,b] делится предварительно на N частей. В подпрограмме Adapt задана абсолютная допустимая погрешность Заметим, что в программе используется завышенная оценка погрешности формулы Симпсона:
Квадратурные формулы интерполяционного типа
Определение формулы интерполяционного типа
В отличие от предыдущих разделов не будем разбивать отрезок интегрирования
где Пример 12.6. При вычислении несобственного интеграла
где Пример 12.7. При вычислении интегралов в бесконечных пределах большое значение имеет закон, по которому функция В частном случае непрерывной подынтегральной функции можем считать Для нахождения коэффициентов аппроксимируем функцию
Подставим интерполяционный многочлен в формулу (12.17):
Поменяв в этой формуле порядок интегрирования и суммирования, придем к формуле (12.17), где
Формула (12.17) называется квадратурной формулой интерполяционного типа, если ее коэффициенты определяются соотношением (12.18). Из равенства (12.18) видим, что особенности подынтегральной функции отражены уже в значениях коэффициентов Примерами формул интерполяционного типа являются рассмотренные ранее квадратурные формулы: прямоугольников, трапеций и Симпсона.
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 660; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.158.29 (0.01 с.) |

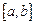 разбивается на подотрезки такой длины, при которой обеспечивается требуемая точность вычислений. Пусть требуется вычислить интеграл
разбивается на подотрезки такой длины, при которой обеспечивается требуемая точность вычислений. Пусть требуется вычислить интеграл
 равна
равна ,
, – результат приближенного вычисления интеграла на отрезке длиной
– результат приближенного вычисления интеграла на отрезке длиной  ,
, – результат вычислений при делении отрезка на два подотрезка половинной длины
– результат вычислений при делении отрезка на два подотрезка половинной длины 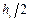 ,
, ,
, – допустимая погрешность вычислений интеграла на всем отрезке
– допустимая погрешность вычислений интеграла на всем отрезке  . Если подынтегральная функция не достаточно гладкая, то порядок квадратурной формулы становится неизвестным.
. Если подынтегральная функция не достаточно гладкая, то порядок квадратурной формулы становится неизвестным. . Начальное число подотрезков выбрано равным N=10. Если при выбранном значении N погрешность слишком велика, количество подотрезков удваивается до тех пор, пока требуемая точность не будет достигнута.
. Начальное число подотрезков выбрано равным N=10. Если при выбранном значении N погрешность слишком велика, количество подотрезков удваивается до тех пор, пока требуемая точность не будет достигнута.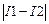 – вместо
– вместо  , как это следует из формулы Рунге. Поэтому для гладких подынтегральных функций программа дает завышенную точность. Однако, завышенная оценка погрешности во многих случаях позволяет избежать ошибок, если подынтегральная функция имеет какие-либо особенности.
, как это следует из формулы Рунге. Поэтому для гладких подынтегральных функций программа дает завышенную точность. Однако, завышенная оценка погрешности во многих случаях позволяет избежать ошибок, если подынтегральная функция имеет какие-либо особенности.
 , (12.17)
, (12.17) – узлы формулы,
– узлы формулы,  – коэффициенты,
– коэффициенты,  – весовая функция. Разбиение подынтегральной функции F на два сомножителя целесообразно, если эта функция имеет какие-либо особенности. В этом случае выделяют интегрируемую на отрезке
– весовая функция. Разбиение подынтегральной функции F на два сомножителя целесообразно, если эта функция имеет какие-либо особенности. В этом случае выделяют интегрируемую на отрезке  .
. ,
,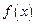 – непрерывная функция, целесообразно функцию
– непрерывная функция, целесообразно функцию 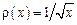 рассматривать как весовую.
рассматривать как весовую. убывает при
убывает при  . При вычислении таких интегралов целесообразно представить подынтегральную функцию в виде
. При вычислении таких интегралов целесообразно представить подынтегральную функцию в виде  , где весовая функция
, где весовая функция  и
и 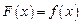 .
. .
.
 . (12.18)
. (12.18)


