
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Квадратурний метод розв'язку інтегральних рівнянь ФредгольмаСодержание книги
Поиск на нашем сайте Як відомо, визначений інтеграл може бути замінений його наближеним значенням, що обчислюються за допомогою квадратурної формули:
де Приведемо значення коефіцієнтів для різних квадратурних формул. Нехай 1. Формула лівих прямокутників:
2. Формула трапецій
3. Формула Симпсона (
Підставивши праву частину наближеного рівності (5.7) із
Вираження (5.8) задає функцію, що описує наближений розв'язок інтегрального рівняння (5.5). Введемо на відрізку
Введемо позначення
Маэмо такий алгоритм знаходження розв'язку рівняння Фредгольма другого роду.
Точність чисельного розв'язку інтегрального рівняння залежить від: - застосовуваної квадратурної формули; – числа вузлів часової сітки; – властивостей функції Для оцінки максимальної апостеріорної погрішності чисельного розв'язку використовують принцип Рунге. Даний принцип полягає в порівнянні чисельних розв'язків, отриманих на часових сітках із кроком Величина погрішності чисельного розв'язку для кожного значення змінної
де p – порядок квадратурної формули, що використовується. Недолік підходу: при даному способі контролю доводиться обмежуватися квадратурними формулами, придатними тільки для сіток з рівномірним кроком. Приклад 5.3. Розв'язати інтегральне рівняння Виконаємо спочатку розрахунки вручну, вибравши на відрізку тільки 3 точки х = [ 0, 0.5, 1]. Замінимо інтеграл квадратурною сумою за методом Симпсона:
Підставляємо останній вираз для інтеграла в рівняння для кожного значення
Візьмемо значення
Рішенням системи є значення Перевіремо це рішення програмно в системі MATLAB.
a=0; b=1; n=3; h=0.5;lambda=1/2; x=a:h:b; b=f1(x); for i=1:n for j=1:n % задаємо коефіцієнти квадратурної формули if (rem(j,2)==1) c=2*h/3; else c=4*h/3; end; if (j==1 || j==n) c=h/3; end; k(i,j)=K1(x(i),x(j)); % обчислюємо коефіцієнті системи рівнянь if (i==j) a(i,j)=1-lambda*c*k(i,j); else a(i,j)=-lambda*c*k(i,j); end; end; end; % розв’язуємо систему і будуємо графік рішення y=a\b' plot(x,y); grid on;
Функції function z=K1(x,t) z=x*t;
function y=f1(x) y=5/6*x;
Точний розв'язок рівняння Загальні відомості про інтегральні рівняння Вольтерра Визначення 3. Лінійним інтегральним рівнянням Вольтера називаються рівняння виду
(рівняння 2-го роду) або виду
(рівняння 1-го роду). В (5.11) і (5.12) Розв'язком рівняння (5.11) будемо називати функцію Метод послідовних наближень розв'язку інтегральних рівнянь Вольтерра Будується послідовність функцій Наступні наближення визначаються за допомогою рекурентного співвідношення:
Якщо ядро Приклад 5.4. Методом послідовних наближень розв'язати рівняння Розв'язок. Прийнявши
У загальному випадку
Звідки
|
||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 642; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |

 (5.7)
(5.7) – номера вузлів сітки по змінній,
– номера вузлів сітки по змінній,  – коефіцієнти квадратурної формули.
– коефіцієнти квадратурної формули. ,
,  .
. .
.

 ):
):
 .
. замість інтеграла в інтегральне рівняння (5.5), одержимо:
замість інтеграла в інтегральне рівняння (5.5), одержимо: (5.8)
(5.8) дискретну часову сітку
дискретну часову сітку  , вузли якої збігаються з вузлами сітки
, вузли якої збігаються з вузлами сітки  . Для кожного моменту часу
. Для кожного моменту часу  виконується рівність:
виконується рівність: ,
,  . (5.9)
. (5.9) ,
,  ,
,  і запишемо (5.9) у вигляді системи
і запишемо (5.9) у вигляді системи  лінійних алгебраїчних рівнянь із
лінійних алгебраїчних рівнянь із  (5.10)
(5.10) у вузлах часової сітки.
у вузлах часової сітки. .
. і
і  в тих самих вузлах часової сітки.
в тих самих вузлах часової сітки. , де
, де  , оцінюється за формулою:
, оцінюється за формулою: ,
,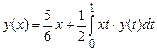 , використовуючи квадратурну формулу Симпсона.
, використовуючи квадратурну формулу Симпсона.
 на обраній сітці й одержуємо таку систему лінійних алгебраїчних рівнянь:
на обраній сітці й одержуємо таку систему лінійних алгебраїчних рівнянь:


 .
. . Збільшення кількості точок на інтервалі не поліпшує якість наближення (це тільки для цього прикладу!).
. Збільшення кількості точок на інтервалі не поліпшує якість наближення (це тільки для цього прикладу!). (5.11)
(5.11)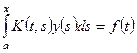 (5.12)
(5.12) – шукана функція, а ядро
– шукана функція, а ядро 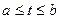 ,
, 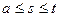 і на відрізку
і на відрізку  , що обертає це рівняння в тотожність. Будемо вважати, що функції
, що обертає це рівняння в тотожність. Будемо вважати, що функції  ,
,  . Нульове наближення
. Нульове наближення  – довільна функція.
– довільна функція. ,
, 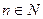 .
. при
при 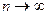 сходиться до єдиного безперервного розв'язку інтегрального рівняння. Звичайно вважають
сходиться до єдиного безперервного розв'язку інтегрального рівняння. Звичайно вважають  .
. .
. , послідовно знаходимо:
, послідовно знаходимо: ,
,  .
. .
. .
.


