
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Погрішність вирішення й збіжністьСодержание книги
Поиск на нашем сайте
Як відомо, збіжність вирішення задач, отриманих сітковими різницевими методами, визначається формулою: Збіжність = Апроксимація + Стійкість. Як було показано вище, крайова задача апроксимується різницевою схемою із другим порядком точності щодо кроків сітки. Стійкість різницевої схеми для рівнянь еліптичного типу випливає із принципу максимуму, який виконується при певних обмеженнях на коефіцієнти рівняння [1]. Отже, буде мати місце збіжність, що означає: 1) система лінійних алгебраїчних рівнянь, що отримана при апроксимації крайової задачі різницевою задачею, буде мати єдиний розв'язок; 2) при зменшенні кроку сітки розв'язок різницевої задачі буде наближуватись до точного розв'язку диференціальної крайової задачі. Практична оцінка погрішності розв'язку крайової задачі може бути отримана за правилом Рунге. Нехай у загальному випадку є формула
Проведемо тепер розрахунок по тій же наближеній формулі для тієї ж точки
Ясно, що Віднімаємо ці дві формули й одержуємо першу формулу Рунге:
Таким чином, розрахунок по другій сітці дозволяє оцінити погрішність на першій сітці. Підставляючи знайдену погрішність у вхідну формулу, одержуємо результат з більш високою точністю по другій формулі Рунге:
Застосовуючи наведені формули до розв'язку задачі Діріхле для рівняння Лапласа методом сіток, бачимо, що необхідно розв'язати задачу двічі – використовуючи сітку із кроком Задача для самостійного вирішення на практиці Задача 2.1. Розв'язати рівняння Завдання до лабораторної роботи Завдання 2.1. Розв'язати задачу Діріхле для рівняння Лапласа у квадраті Завдання 2.2. Виконати завдання 2.1 для Завдання 2.3. Оцінити погрішність вирішення задачі для обраних сіток, використовуючи правило Рунге. Таблиця 2.2 – Варіанти індивідуальних завдань
2.7. Контрольні питання 1. Які види сіток використовуються в методі кінцевих різниць? Яким чином будують на цих сітках різницеві апроксимації рівнянь і відповідні їм шаблони? 2. Які прямі й ітераційні методи використовують для розв'язку систем алгебраїчних рівнянь у задачах з диференційними рівняннями із частинними похідними (ДРЧП)? 3. Дайте характеристику ітераційних методів, що використовуються для розв'язку систем алгебраїчних рівнянь у задачах з ДРЧП. 4. Як задаються граничні умови? Яким чином задається початкове наближення при вирішенні ДРЧП із використанням ітераційних методів? Відповідь поясніть на прикладі. 5. З яких міркувань вибирають крок сітки в методі кінцевих різниць? МЕТОД СІТОК РОЗВ'ЯЗКУ крайових задач для РІВНЯНЬ ПАРАБОЛІЧНОГО ТИПУ Постановка задачі Розглянемо розв'язок змішаної крайової задачі для диференційних рівнянь з частинними похідними (ДРЧП):
с початковою умовою:
і граничними умовами:
Розглянуте рівняння описує розподіл температури в стрижні, початкова температура якого дорівнює значенню функції Для розв'язку задачі методом кінцевих різниць побудуємо прямокутну сітку (рис. 3.1), вузли якої визначаються формулами:
Значення Замінимо частинні похідні в рівнянні теплопровідності їх кінцево-різницевими апроксимаціями в кожному внутрішньому вузлі:
Вираз (3.2) можна вважати наближенням похідної як у точці Вираз (3.3) апроксимує похідну з порядком Для розв'язку змішаної крайової задачі необхідно апроксимувати похідну в граничній умові на правому кінці:
Використовуючи кінцево-різницеву апроксимацію, одержуємо:
Порядок апроксимації останньої формули Явна різницева схема Підставимо вирази (3.2) і (3.3) у рівняння (3.1) і розв'яжемо його щодо значень функції на верхньому часовому шарі:
Формула (3.5) вирішує поставлену задачу, оскільки вона виражає розв'язок у момент часу i+1 через розв'язок у момент часу i. З (3.4) знаходимо: Алгоритм обчислень за явною схемою реалізується наступною послідовністю дій. 1. Обчислюємо значення сіткової функції на першому часовому шарі з початкових умов: 2. Знаходимо розв'язок на сітковому шарі
3. Обчислюємо величину Завершивши кроки 1-3 одержуємо розв'язок при Недолік явної схеми: якщо крок за часом яка накладає досить жорсткі обмеження на крок за часом ( Приклад 3.1. Обчислити за допомогою явної схеми наближений розв'язок змішаної задачі
с початковою умовою Розв'язок. Формула (3.5) з урахуванням кроків по
Схема стійка, якщо
Рисунок 3.2 – Просторово - часова сітка для прикладу 3.1 З початкових умов одержимо:
із граничних умов одержимо
Підрахуємо значення для
Аналогічно обчислюємо для інших значень u=1.0000 0.6000 0.2000 0.2000 0.6000 1.0000 1.0000 0.6000 0.4000 0.4000 0.6000 1.0000 1.0000 0.7000 0.5000 0.5000 0.7000 1.0000 1.0000 0.7500 0.6000 0.6000 0.7500 1.0000 1.0000 0.8000 0.6750 0.6750 0.8000 1.0000 1.0000 0.8375 0.7375 0.7375 0.8375 1.0000 Графіки розв'язку для всіх моментів часу наведені на рис. 3.3. Початковий розподіл температури позначений на графіку неперервною лінією. Щоб отримати оцінку погрішности рішення, проведемо розрахунки з кроком по координаті в два рази менше, тобто Програма, що виконує розрахунки:
% приклад 5.1 n=11;hx=0.1; m=2*(n-1)+1; ht=0.005; u=zeros(m,n); a=1; sig=a^2*ht/hx^2; x=0:hx:1; u(1,:)=abs(2*x-1); t=0:ht:1; v=abs(2*t-1); plot(t,v, 'LineWidth',2); hold on; grid on for i=1:m-1 u(i+1,1)=1; u(i+1,n)=1; for j=2:n-1 u(i+1,j)=u(i,j)+sig*(u(i,j-1)- end end plot(x,u(5,:),'--o','LineWidth',2) plot(x,u(9,:),':s','LineWidth',2) plot(x,u(13,:),'-.*','LineWidth',2) plot(x,u(17,:),'--<','LineWidth',2) plot(x,u(21,:),'-->','LineWidth',2) % виводимо значення температури для кожного четвертого % шару за часом та кожне друге значення по координаті х u(1:4:m,1:2:n)
Рисунок 3.3 – Графіки розв'язку прикладу 3.1 ( Одержуємо такі значення температури: u = 1.0000 0.6000 0.2000 0.2000 0.6000 1.0000 1.0000 0.6250 0.3750 0.3750 0.6250 1.0000 1.0000 0.6875 0.4922 0.4922 0.6875 1.0000 1.0000 0.7437 0.5850 0.5850 0.7437 1.0000 1.0000 0.7902 0.6605 0.6605 0.7902 1.0000 1.0000 0.8283 0.7222 0.7222 0.8283 1.0000, та графік розвязку на рис. 3.4.
Рисунок 3.4 – Графіки розв'язку прикладу 3.1 з кроками Оцінимо погрішність для часу t=0.1 (остання строка матриці).
Відносна погрішність становить трохи більше 2% від значення функції. У більшості випадків таку погрішність можна вважати припустимою. Неявна різницева схема Для апроксимації диференціального рівняння використовуємо нижній шаблон рисунка 5.1. Вважаємо, що вираз (5.2) апроксимує похідну за часом у момент Маємо таку апроксимацію диференціального рівняння:
Вираз (5.7) записується для кожного внутрішнього вузла стрижня і являє собою систему лінійних алгебраїчних рівнянь для невідомих значень температури в момент часу
Домінування діагональних елементів системи забезпечує стійкість методу прогону для її розв’язку. Така схема стійка без будь яких додаткових обмежень на узгодження кроків за часом і координаті x. Розмір кроків визначається тільки вимогами точності отриманого розв'язку. Оскільки має місце апроксимація крайової задачі порядку
Порядок апроксимації по х крайової задачі зменшився за рахунок апроксимації похідної у крайовій умові Апостеріорна оцінка погрішності може бути отримана за правилом Рунге на основі подвійного прорахунку за формулою (2.7). Використовуючи екстраполяцію Ричардсона можна уточнити отриманий розв'язок, підвищивши точність розв'язку на порядок (формула (2.8)).
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 778; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.107.243 (0.009 с.) |

 для обчислення
для обчислення  за значеннями на рівномірній сітці із кроком
за значеннями на рівномірній сітці із кроком  , а залишковий член цієї формули має таку структуру:
, а залишковий член цієї формули має таку структуру: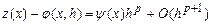 .
. , але використовуючи рівномірну сітку з іншим кроком
, але використовуючи рівномірну сітку з іншим кроком  . Тоді одержимо:
. Тоді одержимо: .
. .
. (2.7)
(2.7) (2.8)
(2.8)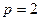 , отже, у знаменнику дроби (2.7) буде число 3. У чисельник підставляємо різницю розв'язків, що отримані у відповідних точках при розрахунку з різними кроками.
, отже, у знаменнику дроби (2.7) буде число 3. У чисельник підставляємо різницю розв'язків, що отримані у відповідних точках при розрахунку з різними кроками. в області
в області  із граничними умовами
із граничними умовами  .
. з вершинами
з вершинами  ,
,  ,
,  ,
,  з граничними умовами, наведеними в таблиці 2.2. Обрати сітку з кількістю точок розбивки
з граничними умовами, наведеними в таблиці 2.2. Обрати сітку з кількістю точок розбивки  по кожній зі змінних. Знайти наближене вирішення задачі із заданою точністю розв'язку системи алгебраїчних рівнянь
по кожній зі змінних. Знайти наближене вирішення задачі із заданою точністю розв'язку системи алгебраїчних рівнянь 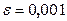 .
. .
.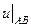



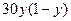
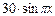










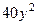









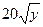
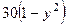




 ,
,  ,
,  (3.1)
(3.1) ,
, 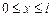
 ,
,  ,
, 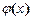 . Температура на лівому кінці стрижня змінюється за законом
. Температура на лівому кінці стрижня змінюється за законом  , на правому кінці стрижня відбувається теплообмін з навколишнім середовищем, температура якого визначається функцією
, на правому кінці стрижня відбувається теплообмін з навколишнім середовищем, температура якого визначається функцією  .
. ,
,  ,
,  ,
,  .
. на лівій і нижній границях сітки відомі з початкових і граничних умов. На правій границі відоме значення частинної похідної розв'язку рівняння по змінній
на лівій і нижній границях сітки відомі з початкових і граничних умов. На правій границі відоме значення частинної похідної розв'язку рівняння по змінній  , (3.2)
, (3.2) (3.3)
(3.3)
 так і в точці
так і в точці  порядку
порядку  .
.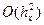 . Таким чином, порядок апроксимації диференційного рівняння
. Таким чином, порядок апроксимації диференційного рівняння 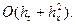
 .
. (3.4).
(3.4). .
. . (3.5)
. (3.5) . (3.6)
. (3.6) .
.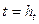 , використовуючи явну формулу:
, використовуючи явну формулу: ,
,  ,
,  .
. за формулою (3.6)
за формулою (3.6)  .
. повторюють кроки 2,3, збільшивши
повторюють кроки 2,3, збільшивши  на одиницю й використовуючи
на одиницю й використовуючи  виявляється досить великим у порівнянні із кроком по
виявляється досить великим у порівнянні із кроком по  ,
, ) і веде до значного збільшення часу для отримання рішення. Така схема називається умовно стійкою.
) і веде до значного збільшення часу для отримання рішення. Така схема називається умовно стійкою. ,
,  ,
,  ,
,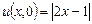 й граничними умовами
й граничними умовами  .
. -
-  і по
і по  -
-  після перетворень прийме вигляд:
після перетворень прийме вигляд: .
. . Перевіримо:
. Перевіримо: 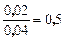 , тобто обрана різницева схема є стійкою.
, тобто обрана різницева схема є стійкою.
 ,
, 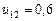 ,
,  ,
,  ,
,  ,
,  ;
; ,
,  ;
;  ,
,  ;
; 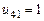 ,
,  .
. :
: ;
;


 , та з кроком за часом в чотири рази менше, тобто
, та з кроком за часом в чотири рази менше, тобто  . (Рішення з кроком за часом
. (Рішення з кроком за часом  виявилось нестійким, дуже швидко зростала погрішність!)
виявилось нестійким, дуже швидко зростала погрішність!)
 ).
).

 ,
, . Тоді й другу похідну по х в (5.3) беремо в тому ж часовому шарі. Схема відповідає нижньому шаблону, наведеному на рисунку 5.1.
. Тоді й другу похідну по х в (5.3) беремо в тому ж часовому шарі. Схема відповідає нижньому шаблону, наведеному на рисунку 5.1. (5.7)
(5.7) ):
):
 й стійкість різницевої схеми, то буде мати місце збіжність розв'язку різницевої задачі до розв'язку даної диференціальної задачі:
й стійкість різницевої схеми, то буде мати місце збіжність розв'язку різницевої задачі до розв'язку даної диференціальної задачі:
 .
.


