
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Побудова сітки й апроксимація рівнянняСодержание книги
Поиск на нашем сайте
Розглянемо розв'язок задачі Діріхле (задані значення функції на границі області) рівняння Лапласа
у квадраті
Почнемо зі знайомства з поняттям кінцево-різницева похідна. Похідну функції заміняють виразом
який апроксимує похідну в точці
Складаючи (2.1) і (2.2), одержуємо центральну різницеву похідну:
яка має другий порядок апроксимації, тобто Аналогічно можна одержати апроксимацію другої похідної:
Тепер можна поширити поняття кінцево-різницевої похідної на частинні похідні. Використовуючи розкладання функції двох змінних в ряд Тейлора
знаходимо вирази для кінцево-різницевої апроксимації частинних похідних:
Побудуємо на площині сітку (рис. 2.1). Будемо використовувати такі позначення:
Рисунок 2.1 - Координатна сітка, що використовується для розв'язку рівнянь з частинними похідними еліптичного типу
Замінимо частинні похідні в рівнянні Лапласа їх кінцево-різницевою апроксимацією:
Вважають, що це різницеве рівняння апроксимує вихідне диференціальне з порядком Якщо
В (2.3) усі співвідношення беруться для внутрішніх вузлів сітки, тому що значення функції на границі задані:
Таким чином, (2.3) являє собою систему лінійних алгебраїчних рівнянь, порядок якої збігається з кількістю внутрішніх вузлів сітки. 2.3 Вирішення системи алгебраїчних рівнянь, що одержана в результаті кінцево-різницевої апроксимації рівняння еліптичного типу, є одним з найбільш важких по обчислювальних витратах етапів розрахунків. Для підвищення точності розв'язку доводиться використовувати сітки з великим числом вузлів, на яких формуються досить великі системи − нерідко до декількох тисяч алгебраїчних рівнянь. Одним зі способів зменшення числа вузлів є використання сіток з нерівномірним кроком. При цьому сітку згущають у найбільш важливих з погляду точності ділянках, наприклад, поблизу кутів або отворів. Для розв'язку подібних систем використовують спеціальні методи, що враховують розрідженість матриці коефіцієнтів. Прямі методи (наприклад, метод Гауса) використовувати недоцільно, тому що це приводить до великого об'єму обчислень. З ітераційних методів застосовують метод Якоби (одночасних зсувів) і метод Гауса-Зейделя (послідовних зсувів), а також модифікації останнього, наприклад, метод верхньої релаксації. Система рівнянь (2.3), що зведена до вигляду (2.4), зручна для ітераційних методів. Якщо задати деякі початкові значення розв'язку рівняння Лапласа у вузлах сітки й потім їх послідовно уточнювати відповідно до (2.4), то ітераційний процес буде сходитися до точного розв'язку. Звичайно в якості початкового наближення використовують значення, що дорівнюють середньому арифметичному граничних значень. Недоліком схеми є низька швидкість збіжності ітераційного процесу, яку можна поліпшити, використовуючи спеціальні методи: метод верхньої й нижньої релаксації. У методі верхньої релаксації ітерації виконуються по наступних формулах:
де Таким чином, чисельне вирішення задачі Діріхле методом сіток з розв'язком системи за методом релаксації знаходиться у відповідності з таким алгоритмом: 1. Задати початкові значення величинам 2. Перераховувати значення у всіх внутрішніх точках сітки відповідно до (2.4) і (2.5) доти, поки різниця між значеннями, отриманими на сусідніх ітераціях, не стане менше заданої точності. Приклад 2.1. Розподілення температури Розв'язок. Оберемо кроки сітки по
Побудуємо різницеву схему:
з урахуванням рівності кроків по
Рисунок 2.3 – Сітка для прикладу 2.1. Із граничних умов маємо:
Запишемо отриману систему – (2.4).
1. Задамо величинам 2. Перерахуємо значення у внутрішніх точках, тобто одержимо перше наближення розв'язку системи за методом Зейделя:
3. Підрахуємо друге наближення:
Запишемо матрицю
Повторюємо ітерації доти, поки значення у вузлах сітки будуть відрізнятися на двох сусідніх ітераціях більше, ніж бажана точність розв'язку системи
що можна вважати наближеним розв'язком задачі.
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 520; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.120.112 (0.007 с.) |

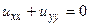 ,
,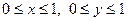 із граничними умовами
із граничними умовами ,
, 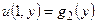 ,
, 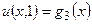 ,
, 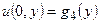 .
.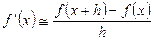 , (2.1)
, (2.1) з точністю до членів порядку
з точністю до членів порядку  . Вираз, що стоїть в правій частині (2.1), називається правою різницевою похідною. В розкладі у ряд Тейлора функції
. Вираз, що стоїть в правій частині (2.1), називається правою різницевою похідною. В розкладі у ряд Тейлора функції 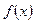 можна замінити
можна замінити 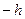 й одержати ліву різницеву похідну:
й одержати ліву різницеву похідну: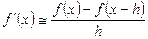 . (2.2)
. (2.2)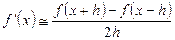 ,
,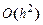 .
.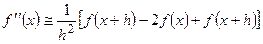 .
.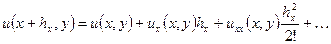 ,
,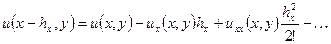 ,
,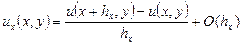 ,
, 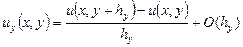 ,
,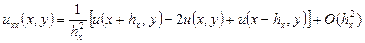 ,
,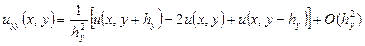 .
.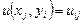 ,
, 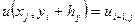 ,
, 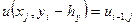 ,
, 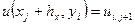 ,
, 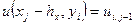 ,
, 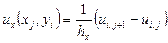 ,
, 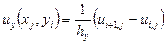 ,
, 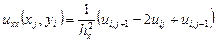 ,
, 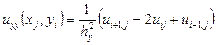 ,
, 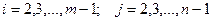

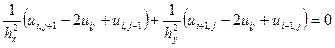 (2.3).
(2.3). .
. (
( у квадраті), то рівняння Лапласа приводиться до виду:
у квадраті), то рівняння Лапласа приводиться до виду: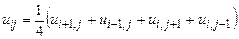 (2.4)
(2.4)
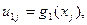
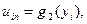
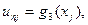
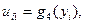
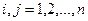 .
.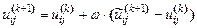 , (2.5)
, (2.5)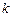 - номер ітерації,
- номер ітерації, 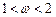 - ітераційний параметр,
- ітераційний параметр, 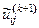 - чергове наближення, отримане за методом Зейделя (формули 2.4).
- чергове наближення, отримане за методом Зейделя (формули 2.4).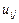 у внутрішніх вузлах сітки (наприклад, рівні середньому значенню всіх граничних умов).
у внутрішніх вузлах сітки (наприклад, рівні середньому значенню всіх граничних умов).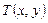 на тонкій пластині прямокутної форми (рисунок 2.2) описується рівнянням Лапласа
на тонкій пластині прямокутної форми (рисунок 2.2) описується рівнянням Лапласа 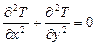 . Знайти значення температури
. Знайти значення температури 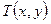 . Розміри
. Розміри 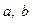 й граничні умови вказані в таблиці 2.1.
й граничні умови вказані в таблиці 2.1. рівними:
рівними:  . В цьому випадку маємо 6 внутрішніх вузлів, в яких треба обчислити температуру (рис. 2.3). Назвемо сіткову функцію
. В цьому випадку маємо 6 внутрішніх вузлів, в яких треба обчислити температуру (рис. 2.3). Назвемо сіткову функцію  .
. Рисунок 2.2 – Пластина прикладу 2.1.
Рисунок 2.2 – Пластина прикладу 2.1.
 ,мм
,мм
 ,мм
,мм
 , °З
, °З
 , °З
, °З

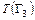 , °З
, °З
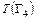 , °З
, °З
 ,
, ) маємо:
) маємо: .
.
 ,
,  ,
,  ,
, 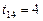 ,
, 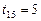 ;
; ,
,  ;
;  ,
,  ;
;  ,
,  ,
,  ,
,  ,
, 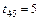 .
.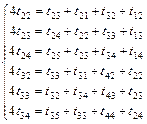 (2.6)
(2.6) .
. ;
; ;
; ;
; ;
; ;
;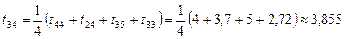 .
.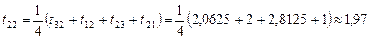 ;
; ;
; ;
;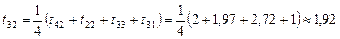 ;
; ;
; .
. другого наближення:
другого наближення: .
.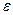 . Нехай
. Нехай  , тоді на шостій ітерації можна вважати, що задана точність розв'язку системи досягнута. Після шостої ітерації матриця розв'язку дорівнює
, тоді на шостій ітерації можна вважати, що задана точність розв'язку системи досягнута. Після шостої ітерації матриця розв'язку дорівнює



