
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Виконання розрахунків у пакеті MATLABСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пакет MATLAB містить додаток PDE Toolbox (від англ.. Partial Differential Equation – диференціальне рівняння із частинними похідними). Додаток забезпечує розв’язок диференціальних рівнянь із частинними похідними методом скінченних елементів у двовимірній постановці. Він включає графічний інтерфейс; інструменти завдання форми рівнянь і граничних умов; процедуру автоматичної генерації сітки скінченних елементів; засоби для візуалізації отриманого розв’язку та його анімації. PDE Toolbox використовує проекційне формулювання методу скінченних елементів. PDE Toolbox являє собою набір спеціальних функцій, що написані на мові MATLAB. Особливе місце серед всіх функцій PDE Toolbox займають pdetool і pdeinit. Під час виклику цих функцій з робочого вікна MATLAB розгортається графічний інтерфейс. Приклад 1.1. Розв’яжемо задачу про ламінарний усталений рух в'язкої нестисливої рідини по призматичному каналу. Розподіл поздовжньої швидкості по перерізу каналу описується рівнянням:
де Граничні умови описують умову прилипання на границі каналу: У разі наявності вільної поверхні усередині каналу поздовжній градієнт тиску дорівнює нулю, тому спонукаючою силою для руху рідини може бути гравітаційна складова, а рівняння для швидкості набуде вигляду:
де
Граничні умови в цьому випадку будуть мати вигляд:
Задачі подібного роду часто зустрічаються при моделюванні теплообмінних апаратів та інших технічних пристроїв. Як приклад розглянемо стаціонарну задачу руху нестисливої в'язкої рідини в коаксіальному зазорі з вільною поверхнею (рис.1.1). Канал нахилений до горизонту під кутом
Рисунок 1.1 – Призматичний канал Знайдемо розв’язок для наступних параметрів:
Розв’язок Математична постановка задачі Рівняння:
Граничні умови:
Координати центрів: Запуск додатку PDE Toolbox Запуск додатку призводить до появи на екрані вікна графічного інтерфейсу. Для цього в командному рядку набираємо: >> pdetool
У верхній частині інтерфейсу рис. 1.2 розташовується рядок головного меню, що включає пункти "File", "Edit" та інші. Безпосередньо під головним меню розміщена панель, що включає інструменти PDETool, список видів завдань "Application" і покажчик значень координат x і y. Нижче розташовані вікно "Set formula" (введення формули) і власне графічне вікно для роботи з зображенням розрахункової області. Внизу є інформаційний рядок "Info" і кнопка "Exit" (вихід).
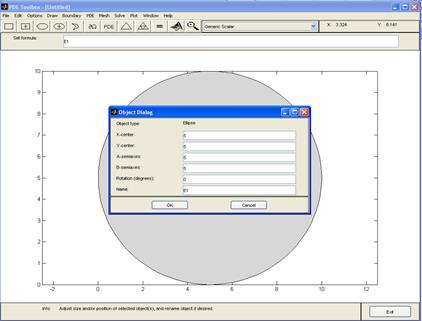
Рисунок 1.2 – Область задачі Перший етап розв’язку На першому етапі необхідносформувати вхідну геометрію задачі в графічному вікні інтерфейсу PDETool. Зображення формуються за допомогою команд пункту Draw (Рисувати) головного меню: Draw Mode – перемикання в режим введення (прорисовки) геометрії; Rectangle/square – створення прямокутника або квадрата за допомогою миші починаючи від його верхньої лівої вершини; Rectangle/square (centered) – створення прямокутника або квадрата за допомогою миші починаючи від його центру; Ellipse/circle – створення еліпса або кола за допомогою миші починаючи від верхньої лівої точки; Ellipse/circle (centered) – створення еліпса або кола за допомогою миші починаючи від центру; Polygon – прорисовка багатокутника відрізками ламаної лінії, поки вона не стане замкнутою; Rotate – поворот виділених об'єктів навколо деякої точки; Export Geometry Description, Set Formula, Labels… – експорт в базову робочу область MATLAB змінних опису геометрії. Для того, щоб нарисувати коло чи квадрат, необхідно натиснути клавішу Shift і вибрати відповідну фігуру. Для того, щоб встановити розмірності області даної задачі, потрібно в меню Option вибрати Axes Limits… У рядку X-axis range набрати [0 10], у рядку Y-axis range набрати [0 10] (рис. 1.2). За допомогою панелі інструментів потрібно нарисувати канал. Спочатку рисуємо коло з центром в точці (0,0) і радіусом 5. Для уточнення координат двічі клацаємо по колу. У вікні Object Dialog встановлюємо параметри (рис. 1.3): X-center 5 Y-center 5 A-semiaxes 5 B-semiaxes 5. Щоб вирівняти осі в меню Option обираємо Axes Equal. Аналогічно рисуємо друге коло з центром в точці (7,3) і радіусом 1, і прямокутник довжини 10 і ширини 1. У рядку Set formula набираємо: E1-E2-R1 (рис. 1.4).
Рисунок 1.3 – Параметри об’єкту Команди для редагування зображення і настройки графічного вікна містяться в наступних пунктах головного меню.
Edit (Правка) містить команди: Undo – скасування останньої дії; Cut – вирізати виділений геометричний об'єкт і помістити його в буфер; Copy – копіювати виділений об'єкт в буфер; Paste – вставити геометричний об'єкт з буфера; Clear – видалити виділений об'єкт; Select All – виділити все геометричні об'єкти. Options (Опції) містить команди: Grid – показати/сховати координатну сітку; Grid Spacing – встановити межі і крок сітки; Snap – округляти координати покажчика миші; Axes Limits – встановити межі координатних осей; Axes Equal – встановити однаковий масштаб по осях x і y; Zoom – показати зі збільшенням виділену частину моделі; Application – перемикання виду задачі; Refresh – оновити зображення моделі.
Рисунок 1.4 – Призматичний канал Другий етап розв’язку Другий етапвключає введення граничних умов на граничних сегментах і параметрів рівняння. Визначити умови на кожному із сегментів можна, виділивши його подвійним клацанням лівої кнопки миші. Відповідні команди розташовуються в розділах Boundary і PDE головного меню. Boundary (Межі) містить команди: Boundary Mode – введення граничних умов; Specify Boundary Conditions… – введення параметрів граничних умов; Show Edge Labels – показати номера граничних сегментів; Show Subdomain Labels – показати номери зон; Remove Subdomain Border – видалити границю зон; Remove All Subdomain Borders – видалення всіх границь зон; Export Decomposed Geometry, Boundary Cond’s… – експорт в робочу область MATLAB змінних опису граничних умов. PDE (Рівняння) містить команди: PDE Mode – перемикання в режим введення параметрів рівняння; Show Subdomain Labels – показати номери зон; PDE Specification… – введення параметрів (коефіцієнтів) рівняння; Export PDE Coefficients… – експорт в базову робочу область змінних, що описують PDE коефіцієнти в розрахунковій області. В меню Boundary оберемо Boundary Mode. Два рази клацаємо по межі Задамо параметри рівняння еліптичного типу, викликавши через меню або панель інструментів вікно "PDE Specification". Оберемо тип рівняння – "Elliptic". Задамо
Рисунок 1.5 – Граничні умови Якщо в списку "Application" установлено режим "Electrostatics" (задача електростатична), то у вікні MATLAB рівняння має вигляд
де діелектрична – діелектрична проникність, У тому випадку, коли встановлено режим "Generic Scalar" у списку "Application" (задача в узагальненій скалярній формі), запис рівняння в MATLAB має вигляд
Рисунок 1.6 – Параметри рівняння Третій етап розв’язку На третьому етапі формується сітка скінченних елементів(рис. 1.7). PDE Toolbox підтримує тільки симплекс-елементи, для яких характерні лінійні функції форми. Пункт Mesh (Сітка) головного меню містить наступні команди: Undo Mesh Change – скасувати останню зміну сітки; Display Triangle Quality – відобразити в кольорі показник регулярності кінцевих елементів; Show Node Labels – показати номери вузлів; Show Triangle Labels – показати номери кінцевих елементів; Parameters… – встановити параметри генератора сітки; Export Mesh – експорт сітки в базову робочу область. Четвертий етап розв’язку Четвертий етап містить власне розв’язок задачі та його вивід у графічному вигляді(рис. 1.8). Відповідні команди розташовуються в пунктах Solve та Plot головного меню. Solve (Розв’язок) містить команди:
Solve PDE – розв’язати крайову задачу; Parameters … – встановити параметри вирішувача; Export Solution… – експорт рішення в базову робочу область. Для отримання ізоліній в меню Plot обираємо Parameters …, де обираємо Contour. Результати розрахунку можна зберегти, звернувшись до пункту File (Файл) меню, що включає команди: New – створити нову модель; Open… – відкрити раніше збережену в m-файлі модель; Save – збереження моделі в m-файлі з поточним ім’ям; Save As… – збереження моделі в m-файлі; Print… – друк рисунка.
Рисунок 1.7 – Формування сітки
Рисунок 1.8 – Розподіл еквіпотенціальних ліній
Приклад 1.2. Розглянемо задачу теплопровідності для прямокутної пластини, поверхня якої теплоізольована, на границях пластини підтримується постійна температура, а на поверхні пластини встановлені джерела тепла, які також мають постійну температуру на границях контакту з пластиною. Пластина має початкову температуру Розв’язок Математична модель задачі буде мати наступний вигляд. Рівняння теплопровідності:
Граничні умови першого роду:
Початкова умова:
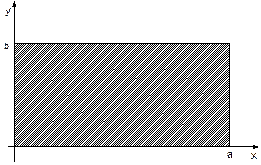
Рисунок 1.9 – Прямокутна пластина
Розрахунок проведемо в безрозмірному вигляді для таких значень параметрів:
Геометричні параметри пластини виберемо такими:
На рис. 1.10 наведено розв’язок задачі для значення
Рисунок 1.10 – Розв’язок задачі із прикладу 1.2
Приклад 1.3. Розглянемо задачу коливань тонкої мембрани. Мембраною називають тонку плівку, яка рівномірно натягнута на контур Г. Нехай в положенні рівноваги мембрана знаходиться в площині xOy та займає деяку область D(x,y). Відомо, що коливання мембрани описується двовимірним диференціальним рівнянням гіперболічного типу
де
які відображають початкове відхилення та початкову швидкість точок мембрани. Гранична умова В якості прикладу розглянемо коливання тонкої мембрани, яка має форму прямокутника.
Рисунок 1.11 – Прямокутна мембрана
Сформулюємо задачу в безрозмірному вигляді наступним чином:
На рис. 1.12 наведено розв’язок задачі для значення
Рисунок 1.12 – Розв’язок задачі із прикладу 1.3
|
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 434; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.190.153.90 (0.008 с.) |

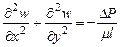 ,
,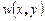 – поздовжня швидкість,
– поздовжня швидкість,  – перепад тиску вздовж осі каналу,
– перепад тиску вздовж осі каналу,  – динамічний коефіцієнт в'язкості.
– динамічний коефіцієнт в'язкості. .
. ,
, – кут нахилу каналу по відношенню до горизонту,
– кут нахилу каналу по відношенню до горизонту,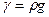 – питома вага рідини.
– питома вага рідини. - на вільній поверхні (n – напрямок нормалі до поверхні);
- на вільній поверхні (n – напрямок нормалі до поверхні);
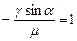 ,
,  м,
м,  м,
м,  м,
м,  м,
м, ,
, ,
, ,
,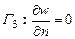 .
. ,
, 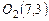 .
.

 , у вікні обираємо Dirihlet,
, у вікні обираємо Dirihlet,  (т.к.
(т.к.  ). Для даної задачі межа
). Для даної задачі межа  . На межі
. На межі  обираємо Neumann,
обираємо Neumann,  .
.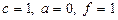 (рис. 1.6).
(рис. 1.6).

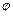 – електричний потенціал,
– електричний потенціал, 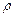 – об’ємний заряд.
– об’ємний заряд. .
.


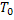 . Геометрія пластини зображена на рис. 1.9.
. Геометрія пластини зображена на рис. 1.9.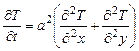 .
. .
. .
.
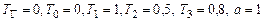 .
. (значення часу
(значення часу  та початкової температури
та початкової температури  потрібно задавати командами Solve/Parameters…).
потрібно задавати командами Solve/Parameters…).
 ,
, ,
,  – натяг мембрани,
– натяг мембрани,  – відхилення мембрани від положення рівноваги. Постановка задачі передбачає початкові умови
– відхилення мембрани від положення рівноваги. Постановка задачі передбачає початкові умови ,
, відображає закріплення мембрани по контуру
відображає закріплення мембрани по контуру  .
.
 ,
,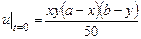 ,
,  .
. потрібно задавати командами Solve/Parameters…).
потрібно задавати командами Solve/Parameters…).



