
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Виконання алгоритму FCM в системі MATLABСодержание книги
Поиск на нашем сайте
Функція fcm може бути викликана в одному з наступних форматів:
або
Вхідними аргументами цієї функції є - data: матриця початкових даних D, і-тий рядок якої являє собою інформацію про об’єкт нечіткої кластеризації - cluster_n: число шуканих кластерів Вихідними аргументами цієї функції є - center: матриця центрів шуканих нечітких кластерів, кожний рядок якої являє собою координати центру одного з нечітких кластерів в формі вектора - U: матриця значень функцій належності шуканого нечіткого розбиття - obj_fun: значення цільової функції (3) на кожній з ітерацій роботи алгоритму.
Функція fcm() може бути викликана з додатковими аргументами options, які введенні для управління процесом кластеризації, а також для зміни критерію останова роботи алгоритму і/або відображення інформації на екрані монітора. Ці додаткові аргументи мають наступні значення: - option (1): експоненційна вага m для розрахунків матриці нечіткого розбиття U (за замовченням - option (2): максимальне число ітерацій s (за замовченням це значення дорівнює 100); - option (3): параметр збіжності алгоритму - option (4): інформація про поточну ітерацію, яка відображається на екрані монітора (за замовченням, це значення 1).
Якщо будь-яке зі значень додаткових аргументів дорівнює NaN (не число), тоді для цього аргументу використовується значення за замовченням.
Приклад реалізації алгоритму Завдання 1. В якості прикладу застосування нечіткої кластеризації розглянемо множину даних, які містяться в системі MATLAB і використовуються в якості текстової сукупності об’єктів нечіткої кластеризації. Ці дані являють собою матрицю D розмірності 140х2 і містяться у файлі fcmdata.dat, який поставляється разом зі MATLAB В даному випадку матриця D відповідає 140 об’єктам, для кожного з який виконане вимірювання за двома ознаками, що є дуже зручним для візуалізації результатів нечіткої кластеризації в двовимірному просторі на площині. 1. Для візуалізації цих даних слід виконати наступні команди: Load fcmdata.dat plot(fcmdata(:,1), fcmdata(:,2), ‘o’) На екрані з’явиться графічне зображення, яке представлене на рис. 6.1.
Рис.6.1 Зображення точок матриці D з файлу fcmdata.dat
2. Далі слід викликати функцію fcm, наприклад, з наступним форматом: [center, U, obj_fcn]=fcm(fcmdata, 2) Потім слід подивитись результати виконання процедури нечіткої кластеризації: - координати центрів класів, тобто, матрицю center; - належність кожної сукупності даних до класів – матрицю U; - значення функції цілі – obj_fcn. Взагалі, процедуру нечіткої кластеризації можна записати у вигляді командного М-файла з наступним текстом: load fcmdata.dat plot(fcmdata(:,1), fcmdata(:,2),’o’) [center, U, obj_fcn]= fcm(fcmdata, 2); maxU=max(U); index1 = find(U(1,:)== maxU); index2 = find(U(2,:)== maxU); line(fcmdata(index1,1), fcmdata(index1,2),’linestyle’,’none’,… ‘marker’, ‘x’, ‘color’, ‘g’); line(fcmdata(index2,1), fcmdata(index2,2),’linestyle’,’none’,… ‘marker’, ‘x’, ‘color’, ‘r’); hold on plot(center(1,1), center(1,2),’ko’, ‘markersize’,10, ‘LineWidth’, 2) plot(center(2,1), center(2,2),’ko’, ‘markersize’,10, ‘LineWidth’, 2)
Результатом цієї програми буде розбиття даних на два кластера, візуалізація якого зображена на рис.6.2.
Рис. 6.2. Результат роботи програми нечіткої кластерізації
3. Після роботи програми в системі MATLAB можна перевірити значення матриць center та U, набравши їх назву в командному рядку і натиснувши Enter. 4. Крім того, в програмі можна використати наступний формат запису: [center, U, obj_fcn]= fcm(fcmdata, 2, [2.5 1000 0.000001 1]); В цьому випадку експоненційна вага 2.5, максимальне число ітерацій 1000, параметр збіжності 5. Для розв’язування задачі нечіткої кластеризації в системі MATLAB можна використовувати графічний інтерфейс, який викликається за допомогою команди findcluster. Ця програма може використовувати або метод с-середніх або метод субтрактивної кластеризації (substractive clustering, який викликається і окремо за допомогою команди subclust). Останній використовується тоді, коли не можна заздалегідь встановити число кластерів с на кроці 6. Формат виклику графічного інтерфейсу: findcluster або findcluster(‘file.dat’).
Рис 6.3. Вікно роботи графічного інтерфейсу нечіткої кластеризації для алгоритму субтрактивної кластеризації
В даному вікні можна завантажити файл даних Load Data, обрати метод кластеризації Methods, обрати необхідні значення параметрів і натиснути кнопку Start.
6. Нехай, заздалегідь невідома кількість кластерів с. Тоді слід використати метод субтрактивної кластеризації. Ідея цього методу полягає у тому, що кожна точка даних пропонується в якості центра потенційного кластеру. Далі слід вирахувати деяку міру можливості кожної точки даних представляти центр кластеру. Ця кількісна міра основана на оцінці густини точок навколо відповідного центра кластера. Цей алгоритм, який є узагальненням методу кластеризації Р. Ягера, заснований на виконанні наступних кроків: 1) вибрати точку даних з максимальним потенціалом для представлення центру першого кластеру 2) забрати всі точки даних в околі центру даного кластеру, величина якої задається параметром radii, щоб визначити наступний нечіткий кластер і координати його центру. Далі, ці дві процедури повторюються до тих пір, допоки всі точки даних не будуть лежати в границях околів радіуса radii навколого шуканих кластерів. Функція командного рядка [C, S] = subclust (X, radii, xBounds, options) знаходить центри таких кластерів. При цьому матриця Х містить об’єкти кластеризації, кожний рядок якої відповідає координатам окремої точки даних. Параметр radii являє собою вектор, компоненти якого приймають значення з інтервалу [0,1] і задають діапазон розрахунку центрів кластерів по кожній з розказ вимірювань об’єктів. Робиться припущення, що всі дані знаходяться в деякому гіперкубі. Взагалі, малі значення параметрів radii призводять до знаходження малого числа великих по кількістю точок кластерів. Найкращих результатів можна очікувати при значенні radii між 0.2 і 0.5. Аргумент xBounds являє собою матрицю розміру (2xq), яка визначає засіб відображення матриці даних Х в деякому одиничному гіперкубі. Тут q – кількість ознак. Цей аргумент є необов’язковим, якщо матриця Х вже нормована. Перший рядок цієї матриці містить мінімальні значення інтервалу вимірювання кожної ознаки, а другий рядок – максимальне значення вимірювання кожної ознаки. Для зміни значень, які встановлені по замовченню, можна використати параметр options, компоненти вектора якого можуть приймати наступні значення: - оptions(1) = guashFactor – параметр, який використовується в якості коефіцієнту для множення значень radii з ціллю зменшення впливу потенціалу граничних точок, які розглядаються як частина даного кластеру (за замовченням це значення дорівнює 1.25); - options(2) = acceptRatio – параметр, який встановлює потенціал як частину потенціалу першого кластеру, вище якого інша точка даних не може розглядатся в якості центра іншого кластеру (за замовченням це значення 0.5); - option(3) = rejectRation - параметр, який встановлює потенціал як частину потенціалу першого кластеру, нижче якого інша точка даних не може розглядатся в якості центра іншого кластеру (за замовченням це значення 0.15); - options(4) = verbose – якщо значення цього параметра не дорівнює 0, тоді на екран монітору виводиться інформація про виконання процесу кластеризації (за замовченням це значення 0). Функція subclust повертає матрицю С значень координат центрів нечітких кластерів. При цьому кожний рядок цієї матриці містить координати одного центру кластеру. Вектор S містить
Для прикладу розглянемо наступну послідовність команд: Load fcmdata.dat [C, S] = subclust(fcmdata, [0.5 0.5], [], [1.25 0.5 0.15 1]) Для кожної ознаки вводяться радіуси околів – 0.5 і 0.5. Як видно з рис. 3. для даної сукупності даних функція suclust має знайти три кластери. Для розв’язування задачі субтрактивної кластеризації може використовуватися і розглянутий раніше графічний інтерфейс, який викликається командою findcluster. Таким чином, система MATLAB дозволяє розв’язувати задачі нечіткої кластеризації двома способами: за допомогою функцій командного рядка і за допомогою графічного інтерфейсу кластеризації. Результати нечіткої кластеризації мають наближений характер і мають служити для попередньої структуризація вхідної (початкової) інформації про систему, що вивчається. Тобто, провівши кластерізацію, можна отримати і зберегти знання про систему у вигляді структуризації початкової інформації.
6.6. Завдання для самостійної роботи 1. Виконати нечітку кластеризації набору точок в двовимірному просторі ознак: (1,2); (2,1); (1, 2); (3,2); (2,3); (1,6); (2,5); (3,6); (5,5); (5,6); (7,5); (7,6). Розділити їх на 3 кластери. Відповідь можна подивитися на рис 6.4.
Рис 6.4. Точки і центри кластерів завдання 1
2. Виконати нечітку кластерізацію 10 фірм, які можуть в майбутньому опинитися в різних зонах своєї діяльності на ринку (2, 3 або 4 зони). Для цього слід використовувати дві ознаки стану фірм – середній дохід і середнє-квадратичне відхилення можливого доходу, тобто, ризикованість. Відомі наступні дані про фірми:
Яка можлива економічна інтерпретація цих зон?
§7. Лабораторна робота №6 РОЗРОБКА ІНТЕЛЕКТУАЛЬНИХ СИСТЕМ НА ОСНОВІ
Мета роботи: освоїти методику проектування і побудови інтелектуальних систем на основі моделей нечітких нейронних мереж.
7.1. Нейроні мережі в Matlab
Концептуальною основою і складовою частиною штучних нейронних мереж є так званий штучний нейрон, що має визначену внутрішню структуру (рис. 7.1) і правила перетворення сигналів (7.1).
Рис. 7.1. Структура штучного нейрона
Штучний нейрон (далі просто — нейрон) складаєтьсяз помножувачів (синапсів), суматора і нелінійного перетворювача. Синапси, зображені перекресленим кружком, призначені для зв'язку нейронів між собою і множать вхідний сигнал Правила перетворення сигналів визначаються математичною моделлю нейрона, що може бути записана у формі наступних аналітичних виразів:
де Синаптичні зв'язки з позитивними вагами: Таким чином, окремо узятий штучний нейрон цілком описується своєю структурою (див. рис. 7.1) і математичною моделлю (7.1). Одержавши вектор вхідного сигналу хi, нейрон видає деяке число y на своєму виході. Як функція активації нейрона можуть бути використані різні нелінійні перетворення (табл. 7.1). Таблиця.7.1. Основні види функцій активації нейронів
Нейронна мережа являє собою сукупність окремих нейронів, взаємозв’язаних між собою деяким фіксованим чином. При цьому взаємозв'язок нейронів визначається чи задається структурою (топологією) нейронної мережі. З точки зору топології нейронні мережі можуть бути повнозв’язними, багатошаровими і слабозв’язними. У загальному випадку структура багатошарової чи багаторівневої нейронної мережі може бути зображена в такий спосіб (рис. 7.2).
Рис. 7.2. Структура трирівневої нейронної мережі Кожний з рівнів нейронної мережі називається її шаром. При цьому шар вхідного рівня називається вхідним шаром, шар рівня 1 і 2 — схованими шарами, а шар рівня 3 — вихідним шаром. У свою чергу багатошарові нейронні мережі можуть бути наступних типів: · Монотонні — кожен шар (крім вихідного) додатково розбивається на 2 блоки: збуджуючий і гальмуючий. Аналогічно розбиваються і зв'язки між блоками: на збуджуючі і гальмуючі. При цьому як функції активації можуть бути використані тільки монотонні функції (див. табл. 7.1). · Нейронні мережі зі зворотними зв'язками — інформація з наступних шарів може передаватися на нейрони попередніх шарів. · Нейронні мережі без зворотних зв'язків — інформація з наступних шарів не може передаватися на нейрони попередніх шарів. Класичним варіантом багатошарової нейронної мережі є повнозв’язна мережа прямого поширення (рис. 7.2). Процес побудовиі використаннянейро-мережевих моделей складаєтьсяз наступних етапів: 1. Вибір типу і структури нейронної мережі для розв’язку поставленої проблеми (синтез структури нейронної мережі). 2. Навчання нейронної мережі (визначення чисельних значень ваг кожногоз нейронів) на основі наявної інформації про розв’язок даної задачі експертом чи даних про розв’язок задачі в минулому. 3. Перевірка нейронної мережі на основі використання деякого контрольного приклада (необов'язковий етап). 4. Використання навченої нейронної мережі для розв’язку поставленої проблеми. В даний час запропоновані різні схеми класифікації нейронних мереж і відповідні алгоритми їх навчання. Одним з найпоширеніших алгоритмів навчання є так званий алгоритм зворотного поширення помилки (back propagation). Цей алгоритм являє собою ітеративний градієнтний алгоритм мінімізації середньоквадратичного відхилення значень виходу від бажаних значень (мінімізації помилки) у багатошарових нейронних мережах. Вибір виду і структури нейронної мережі визначається специфікою розв'язуваної задачі. При цьому для розв’язку окремих типів практичних задач розроблені оптимальні конфігурації нейронних мереж, що найбільше адекватно відбивають особливості відповідної проблемної області. Подальшим розвитком нейронних мереж є так звані гібридні мережі, що реалізовані в пакеті Fuzzy Logic Toolbox системи МАТLАВ. Гібридна мережа являє собою багатошарову нейронну мережу спеціальної структури без зворотних зв'язків, у якій використовуються звичайні (не нечіткі) сигнали, ваги і функції активації, а виконання операції підсумовування (7.1) засновано на використанні фіксованої Т-норми, Т-конорми чи деякої іншої неперервної операції. При цьому значення входів, виходів і ваг гібридної нейронної мережі являють собою дійсні числа з відрізка [0, 1]. Основна ідея, покладена в основу моделі гібридних мереж, полягає в тому, щоб використовувати існуючу вибірку даних для визначення параметрів функцій належності, що найкраще відповідають деякій системі нечіткого виводу. При цьому для находження параметрів функцій належності використовуються відомі процедури навчання нейронних мереж. У пакеті Fuzzy Logic Toolbox системи МАТLАВ гібридні мережі реалізовані у формі так званої адаптивної системи нейро-нечіткого виводу ANFIS. З одного боку, гібридна мережа ANFIS являє собою нейронну мережу з єдиним виходом і декількома входами, що являютьсобоюнечіткі лінгвістичні змінні. При цьому терми вхідних лінгвістичних змінних описуються стандартними для системи МАТLАВ функціями належності, а терми вихідної змінної представляються лінійною чи постійною функцією належності. З іншого боку, гібридна мережа ANFIS являє собою систему нечіткого виводу FIS типу Сугено нульового чи першого порядку, у якій кожне з правил нечітких продукцій має постійну вагу, рівну 1. У системі МАТLАВ користувач має можливість редагувати і налаштовувати гібридні мережі ANFIS аналогічно системам нечіткого виводу, використовуючи всі розглянуті раніше засоби пакета Fuzzy Logic Toolbox. У пакеті Fuzzy Logic Toolbox системи МАТLАВ гібридні мережі реалізовані у формі адаптивних систем нейро-нечіткого виводу ANFIS. При цьому розробка і дослідження гібридних мереж виявляється можливою: · інтерактивному режимі за допомогою спеціального графічного редактора адаптивних мереж, що одержав назву редактора ANFIS; · режимі командного рядка за допомогою введення імен відповідних функцій з необхідними аргументами безпосередньо у вікно команд системи МАТLАВ. Для роботи в режимі командного рядка призначені спеціальні функції. Редактор ANFIS дозволяє створювати чи завантажувати конкретну модель адаптивної системи нейро-нечіткого виводу, виконувати її навчання, візуалізувати її структуру, змінювати і налагоджувати її параметри, а також використовувати налагоджену мережу для одержання результатів нечіткого виводу. Графічний інтерфейс редактора ANFIS викликається функцією anfisedit зкомандного рядка середовища Matlab.
7.2. Приклад розв’язку задачі нейро-нечіткого виводу
Для ілюстрації процесу розробки гібридної мережі в системі МАТLАВ розглянемо задачу побудови адаптивної системи нейро-нечіткого виводу для апроксимації деякої виробничої функції типу Кобба-Дугласа:
яка описує залежність між витратами двох виробничих факторів (наприклад, грошей і праці) у кількості Загальна послідовність процесу розробки моделі гібридної мережі може бути представлена в наступному вигляді. Крок 1. Для початку за допомогою редактора відладчика m-файлів або будь-якого текстового редактору підготуємо навчальні дані, що містять 6-ти рядків з трьох значень – два вхідних і одне вихідне значення, наприклад, наступного виду: 1 2 2.37 4 1 4.00 1 4 2.82 5 5 6.68 2 4 4.00 4 3 5.26 3 1 3.46 4 4 5.65 4 2 4.80 Числа в рядку розділяються клавішею «Space», а перехід на наступний рядок відбувається натисненням клавіші «Enter». Слід зберегти цей файл у папці work каталогу Matlab6, наприклад, з назвою train.txt. Взагалі, вхідні дані представляють собою звичайну числову матрицю розмірності m´(n+ 1 ), у якій кількість рядків m відповідає обсягу вибірки, перші п стовпців — значенням вхідних змінних моделі, а останній стовпчик — значенню вихідної змінної. Відповідно до правил системи МАТLАВ окремі значення матриці відокремлюються пробілами, а кожен рядок матриці завершується символом "перевід каретки" (клавіша <Enter>). Хоча по кількості рядків матриці вхідних даних не існує формальних рекомендацій, прийнято вважати, що якість навчання гібридної мережі, а, отже, і точність одержуваних результатів пропорційно залежить від обсягу навчальної вибірки. Що стосується кількості стовпців матриці вхідних даних, то слід зазначити можливі проблеми з працездатністю системи МАТLАВ, якщо кількість вхідних змінних перевищує 5 — 6. Початкові дані, що завантажуються, можуть бути одного з наступних типів: · навчальні дані (Training) — обов'язкові дані, що використовуються для побудови гібридної мережі; · тестові дані (Testing) — необов'язкові дані, що використовуються для тестування побудованої гібридної мережі з метою перевірки якості функціонування побудованої гібридної мережі; · перевірочні дані (Checking) — необов'язкові дані, що використовуються для перевірки побудованої гібридної мережі з метою з'ясування факту перенавчання мережі; · демонстраційні дані (Demo) — дозволяють завантажити один з демонстраційних прикладів гібридної мережі. Тому, створимо ще і файл тестових даних test.txt. За аналогією зі створенням файлу train.txt, введемо в нього наступні дані: 2 1 2.82 3 2 4.12 1 3 2.63 2 3 3.72 3 3 4.56 4 2 4.75 3 4 4.90
Крок 2. Головне меню редактора ANFIS достатньо просте і призначене для роботи з попередньо створеною системою нечіткого виводу. Основну частину графічного інтерфейсу займає вікно візуалізації даних, що розташоване нижче головного меню (рис. 7.3). Для знову створюваної гібридної мережі це вікно не містить ніяких даних. Для створення гібридної мережі необхідно завантажити дані. Для цієї мети слід скористатися кнопкою Load Data в лівій нижній частині графічного вікна. При цьому дані можуть бути завантажені з зовнішнього файлу (disk) чи з робочої області (worksp). У першому випадку необхідно попередньо створити файл із вхідними даними (файл train), що являє собою звичайний текстовий файл. Після завантаження файлу із навчальними даними в редактор АNFIS у робочому вікні редактора буде зображений графік, ордината якого відображає значення вхідної математичної функції (кількість продукції у прикладі).
Рис. 7.3. Графічний інтерфейс редактора ANFIS після завантаження файлу function.dat з навчальними даними Завантажимо ще і тестові дані для перевірки. Для цього в лівому нижньому кутку екрану оберемо тип testing, натиснемо кнопку Load data і завантажимо файл test.txt. Крок 3. Приступити до генерації структури системи нечіткого виводу FIS. Ця структура аналогічна структурі системи нечіткого виводу типу Сугено. Тобто, має в своєму складі лінгвістичні вхідні змінні; вихідну змінну, терми якої представляються у вигляді числових констант або лінійних функцій від вхідних змінних; систему правил виводу. Крім того, можна завантажити структуру уже створеної FIS з диска (Load from disk), або з робочої області (Load from worksp). При створенні структури нової FIS можна незалежно розбити усі вхідні змінні на області їх значень (Grid partision) чи скористатися процедурою субтрактивної кластеризації для попередньої розбивки значень вхідних змінних на кластери близьких значень (Sub. clustering). Після натискання кнопки Generate FIS викликається діалогове вікно з вказівкою числа і типу функцій належності для окремих термів вхідних змінних і вихідної змінної (рис. 7.4). В цьому вікні можна вибрати тип функцій належності і кількість термів кожної вхідної змінної, а також тип вихідної змінної. Установивши параметри генерації, наприклад, як на рис.7.4, одержимо структуру FIS.
Рис. 7.4. Діалогове вікно для завдання кількості і типу функцій належності
Після генерації структури гібридної мережі можна її подивитись, натиснувши кнопку Structure в правій частині графічного вікна. Структура отриманої в результаті системи нечіткого виводу FIS відображається в окремому вікні і досить тривіальна по своєму виду. Проаналізуйте її зміст. Крок 4. Перед навчанням гібридної мережі необхідно задати параметри навчання, для чого варто скористатися наступною групою опцій у правій нижній частині робочого вікна: 1. Вибрати метод навчання гібридноїмережі — зворотного розповсюдження (bacprоро) чи гібридний (hybrid),що представляє собою комбінацію мeтоду найменших квадратів і методу спадання зворотного градієнта. 2. Установити рівень помилки навчання (Error Tolerance) — за замовчуваннямзначення 0 (змінювати не рекомендується). 3. Задати кількість циклів навчання (Epochs) — за замовчуванням значення 3 (рекомендується збільшити і для розглянутого приклада задати його значення рівним 40). 6. Для навчання мережі варто натиснути кнопку Trian Now. При цьому хід процесу навчання ілюструється у вікні візуалізації у формі графіка — залежність помилки від кількості циклів навчання. 7. Аналогічно можуть бути виконані додаткові етапи тестування й перевірки гібридної мережі, для яких необхідно попередньо завантажити відповідні дані. Крок 5. Подальше настроювання параметрів побудованої і навченої гібридної мережі може бути виконане за допомогою розглянутих раніше стандартних графічних засобів пакета Fuzzy Logic Toolbox. Для цього рекомендується зберегти створену систему нечіткого виводу в зовнішньому файлі з розширенням fis, після чого варто завантажити цей файл у редактор систем нечіткого виводу FIS. Можна працювати зі структурою системи нечіткого виводу безпосередньо в редакторі ANFIS. При цьому також стають доступними редактор функцій належності системи нечіткого виводу (Membership Function Editor), редактор правил системи нечіткого виводу (Rule Editor), програма перегляду правил системи нечіткого виводу (Rule Viewer) і програма перегляду поверхні системинечіткоговиводу (Surface Viewer). Проаналізуйте правила та функції належності, які були побудовані даною системою апроксимації виробничої функції. Спробуйте їх корегувати і слідкувати за зміною результатів.
Крок 6. Виконати аналіз точності побудованої нечіткої моделі гібридної мережі можна за допомогою перегляду поверхні відповідної системи нечіткого виводу. Для цього слід записати побудовану мережу у вигляді файлу з розширенням *.fis і завантажити його в системі нечіткого виводу fuzzyToolbox (рис.5).
Рис. 7.5. Графічний інтерфейс пергляду поверхні згенерованої системи нечіткого виводу Візуальний аналіз зображеного графіка з точним графіком функції Аналіз адекватності побудованої моделі можна виконати за допомогою перегляду правил відповідної системи нечіткого виводу (рис.7.6). Перевірка побудованої моделі гібридної мережі може бути виконана для декількох значень вихідної змінної. З цією метою необхідно ввести конкретне значення в поле вводу Input (наприклад, значення 3 1), після натискання клавіші <Enter> за допомогою побудованої моделі буде отримане відповідне значення вихідної змінної (у даному випадку значення 3.46). Порівнюючи отримане значення з точним значенням функції 3.46, одержимо відносну помилку порядку 0%.
Рис. 7.6. Графічний інтерфейс перегляду правил згенерованої системи нечіткого виводу Менш удалою виявляється перевірка для значення вхідних змінних 4 3, для якого побудована модель пропонує значення 5.45 (табличне значення 5.26). Очевидно, даний факт свідчить не на користь адекватності побудованої нечіткої моделі і вимагає її додаткового настроювання. У загальному випадку додаткове настроювання моделі може бути виконане декількома можливими способами. Найбільш прийнятними з них представляються наступні. 1. Підготовка і завантаження більшогоза обсягом вибірки файлу з навчальними вхідними даними. 2. Підготовка і завантаження додаткового файлу з перевірочними вхідними даними, сформованими для пар значень розглянутої математичної функції, відсутніх у вибірці навчальних даних. 3. Редагування типів і значень параметрів функцій належності термів вхідної і вихідної змінних за допомогою редактора функцій належності системи МАТLАВ. Проілюструємо третій спосіб додаткового настроювання побудованої нечіткої моделі гібридної мережі. На перший погляд він представляється найбільш природним з погляду можливості візуального контролю виконуваних змін параметрів. З цією метою відкриємо редактор функцій належності і методом підбора змінимо кількісні значення параметрів другої і третьої функції належності вхідної змінної, оскільки саме вони "працюють" при одержанні некоректного значення вихідної змінної: 5.45 для значення вхідних змінних 4 і 3. (рис.7.7).
Рис. 7.7. Графічний інтерфейс редактора функцій належності побудованої системи нечіткого виводу
Після зміни параметрів у полі Params для третьої функції належності першої змінної на значення [0.385 3.66] одержимо практично точне значення вихідної змінної для значення вхідної змінної 5.29 (рис.7.8).
Рис. 7.8. Результат ручного настроювання параметрів функції належності вхідної змінної для розглянутої системи нечіткого виводу
Більш ефективним способом настроювання, а точніше — модифікації, даної нечіткої моделі виявляється перший. З цією метою можна збільшити обсяг навчальної вибірки до 12 пар значень, додавши ще три рядка в файл train.txt. Наприклад:
2 1 2.82 3 2 4.12 1 3 2.63
Після видалення усіх раніше завантажених даних кнопкою Clear Data завантажимо новий файл із навчальною вибіркою. При генерації структури нової FIS збільшимо кількість термiв і, відповідно, кількість функцій належності вхідної змінної до 5, залишивши їх тип без зміни (gbellmf). Процес навчання виконаємо аналогічно раніше розглянутому. У результаті буде отримана нова система нечіткого виводу FIS, аналіз якої показує, що в порівнянні з першим варіантом нечіткої моделі вона більш точно описує вихідну математичну функцію. Це може бути основою для генерації нової нечіткої моделі, що пропонується виконати самостійно як вправу. На закінчення необхідно відзначити, що навіть найпростіші розглянуті приклади відбивають творчий характер процесу побудови й аналізу моделей гібридних мереж. При цьому вибір того чи іншого способу додаткового настроювання нечітких моделей залежить не тільки від специфіки розв'язуваної задачі, але і від обсягу доступної вибірки навчальних і перевірочних даних. У випадку недостатньої інформації навчальних даних використання гібридних мереж може виявитися взагалі недоцільним, оскільки одержати адекватну нечітку модель, а значить — і точний прогноз значень вихідної змінної не представляється можливим. Саме з цих причин необхідний попередній аналіз усіх можливостей застосовуваних нечітких моделей для рішення конкретних задач у тій чи іншій проблемній області. Подібний аналіз необхідно виконувати із системної точки зору і з обліком всіх обставин, що складаються на даний момент. Тільки всебічна і повна оцінка проблемної ситуації дозволить розробити адекватну модель розв'язку тієї чи іншої конкретної задачі нечіткого керування чи прийняття рішень. 7.3. Завдання для самостійної роботи. 1. Апроксимація поверхні. За допомогою гібридної мережі провести апроксимацію залежності
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 1144; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.017 с.) |


 .
. у формі вектора
у формі вектора 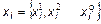 ;
; .
. ;
; ;
; );
); (за замовченням це значення дорівнює 0.00001);
(за замовченням це значення дорівнює 0.00001);

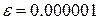 . Порівняльний аналіз показує практичну ідентичність графіків – результатів використання обох форматів функції fcm, що дозволяє зробити висновок про відповідність отриманих результатів нечіткої кластеризації.
. Порівняльний аналіз показує практичну ідентичність графіків – результатів використання обох форматів функції fcm, що дозволяє зробити висновок про відповідність отриманих результатів нечіткої кластеризації.
 -значень, які визначають діапазон впливу центра кластеру по кожній з розглянутих ознак. При цьому, всі центра кластерів мають однакову множину
-значень, які визначають діапазон впливу центра кластеру по кожній з розглянутих ознак. При цьому, всі центра кластерів мають однакову множину 

 на деяке постійне число. Це число
на деяке постійне число. Це число  , назване вагою синапса, характеризує силу цьогозв'язку. Суматор виконує додавання всіх сигналів, що надходять на вхід нейрона від інших нейронів, і зовнішніх вхідних сигналів. Нелінійний перетворювач призначений для нелінійної зміни вихідного значення суматора відповідно до деякої функції від одного аргументу. Ця функція називається функцією активації чи передатною функцією нейрона.
, назване вагою синапса, характеризує силу цьогозв'язку. Суматор виконує додавання всіх сигналів, що надходять на вхід нейрона від інших нейронів, і зовнішніх вхідних сигналів. Нелінійний перетворювач призначений для нелінійної зміни вихідного значення суматора відповідно до деякої функції від одного аргументу. Ця функція називається функцією активації чи передатною функцією нейрона.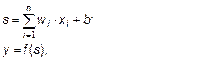 (7.1)
(7.1) — вага синапса
— вага синапса  ; b — значення зсуву; s — результат підсумовування;
; b — значення зсуву; s — результат підсумовування;  — компонент вектора чи входу вхідного сигналу
— компонент вектора чи входу вхідного сигналу  ; у — вихідний сигнал нейрона; п — число входів нейрона; f — функція активації (передатна функція) нейрона, що представляє собою деяке нелінійне перетворення. У загальному випадку:
; у — вихідний сигнал нейрона; п — число входів нейрона; f — функція активації (передатна функція) нейрона, що представляє собою деяке нелінійне перетворення. У загальному випадку:  .
. називаються збуджуючими, а з негативними вагами
називаються збуджуючими, а з негативними вагами 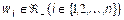 гальмуючими.
гальмуючими.



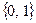
















 ,
, і
і  та кількістю виготовленої продукції
та кількістю виготовленої продукції  у наперед визначених одиницях.
у наперед визначених одиницях.





 , використовуючи дані, я
, використовуючи дані, я 


