
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Завдання 4. Нечітка модель керування контейнерним краном.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Контейнерні крани використовуються при виконанні вантажних робіт в портах. Крани тросом підіймають контейнер з вантажем і далі ідуть на спеціальних рейсах до місця призначення і там розвантажуються. Коли контейнер піднімається до крану і кран починає рухатися по рейсам, вантаж починає розхитувати і відхилятися від свого строго вертикального положення під краном. Проблема полягає в тому, що допоки контейнер хитається, він не може бути опущений на платформу цілі, в якості яких використовуються деякі транспортні засоби. Аналіз дій крановиків-операторів, які виконують дії по управлінню краном, показує, що вони в своїй роботи використовують наступні евристичні правила: Почати роботу, потрібно, коли контейнер вже завантажено грумом і виконувати наступні правила: 1. Якщо контейнер знаходиться на горизонталі завантаження чи цілі (наприклад, це позиція 0), тоді слід підняти контейнер на рівень руху (наприклад, позиція 1). 2. Починати рух потрібно зі середньою потужністю 3. Якщо рух вже почався, кабіна знаходиться далеко від цілі і контейнер несильно хитається, тоді потрібно задати потужність руху велику 4. Якщо рух вже почався, кабіна знаходиться далеко від цілі і контейнер сильно хитається, тоді потрібно задати потужність руху невелику 5. Якщо кабіна знаходиться близько від цілі, слід зменшити швидкість руху до малої 6. Якщо контейнер знаходиться дуже близько до цілі, тоді слід виключити потужність двигуна 7. Коли контейнер знаходиться прямо над позицією цілі, тоді слід зупинити двигун. 8. Якщо контейнер знаходиться над ціллю, але хитання великі, тоді слід не опускати контейнер на ціль і чекати 9. Якщо контейнер знаходиться над ціллю, він не хитається, тоді слід опускати його 10. Якщо контейнер зустрівся з ціллю, тоді слід зупинити його опускання
Крок 1. Визначити вхідні і вихідні змінні. Очевидно, що для СНВ у якості вхідних змінних потрібно взяти відстань до цілі, кут хитання контейнеру від строго вертикальної позиції під кабіною крану і вертикальну відстань контейнеру від цілі.. У якості вихідних змінних слід взяти потужність двигуна крана при русі рейсами і швидкість опускання, чи піднімання крану. Далі слід задати терми цих змінних. Наприклад, для 1 вхідної змінної – «відстань далека», «відстань середня», «відстань близька», «позиція над ціллю», для 2 вхідної змінної – «кут=0», «кут хитання малий», «кут хитання великий», для 3 вхідної змінної – «контейнер в позиції 0», «контейнер в позиції 1», для 1 вихідної змінної – «потужність середня», «потужність велика», «потужність мала», «потужність нульова», для 2 вихідної змінної – «піднімати контейнер», «опускати контейнер», «не змінювати вертикальну позицію контейнера»
Крок 2. Фазіфікація вхідних змінних. На цьому кроці слід задати функції належності для всіх термів вхідної змінної, а в якості області визначення – інтервал можливих значень. Крок 3. Задати функції належності термів вихідних змінних. Крок 4. Ввести правила у базу правил. Крок 5. Використання моделі. Для цього розглянути приклад роботи системи керування при різних значеннях вхідної змінної.
Рис 4.10. Наближений вигляд поверхні задачі про кондиціонер
Рис 4.11. Наближений вигляд поверхні задачі контейнера
§5. Лабораторна робота № 4 РОЗРОБКА НЕЧІТКИХ МОДЕЛЕЙ СИСТЕМ ПІДТРИМКИ ПРИЙНЯТТЯ
Мета роботи: Освоїти методику проектування і побудови систем підтримки прийняття рішень на основі моделі нечіткого виводу та бази знань нечітких продукцій, на прикладі системи оцінюваннія фінансової заможності клієнтів з боку банків при видачі довгострокових кредитів. На цьому прикладі познайомитися з особливостями розробки практично ефективних додатків - програмних засобів нечіткого моделювання. 5.1 Змістовна постановка задачі оцінювання фінансової Суть розглянутої задачі полягає в наступному. При видачі довгострокових кредитів на будівництво будинків чи котеджів під заставу нерухомості для оцінки заможності клієнтів банками традиційно використовується метод експертних оцінок. При цьому метою банків є одержання максимального прибутку від укладених угод по наданню кредитів і виключення можливості фінансових утрат.Тому інтереси банків зосереджені, з одного боку, на збільшенні кількості успішних угод, а з іншого боку, на запобіганні невдалих угод, коли клієнт не повертає виданий кредит чи повертає його не вчасно.
Традицiйно підставою для прийняття рішень по наданню кредитів у майбутньому служить досвід успішних угод, зроблених у минулому. Керівництво банку Ноme&Sevings Ваnk, в інтересах якого виконувалося відповідне дослідження, хотіло б узагальнити правила надання кредитів з метою максимально повно використовувати досвід експертів. При цьому необхідно виключити можливі помилки суб'єктивного характеру з боку окремих менеджерів у випадку неадекватного оцінювання фінансової заможності клієнтів. Аналіз стратегії надання кредитів на будівництво будинків показує, що для оцінювання фінансової заможності клієнтів можуть бути використані різні характеристики, такі як місцезнаходження споруджуваного будинку, якість передбачуваного виконання опоряджувальних робіт, оцінка активів потенційного клієнта, оцінка доходу потенційного клієнта за винятком фіксованих витрат, величина підлягаючих сплаті відсотків з кредиту. При цьому власне фінансова заможність клієнта оцінюється його кредитоспроможністю. Однією з перших формальних моделей, запропонованих для розв’язку даної задачі, була статистична модель, заснована на імовірнісній інтерпретації кількісної оцінки позитивного рішення про надання кредиту. Однак більш детальний аналіз цієї моделі згодом показав її неадекватність, пов’язану з недостатнім обсягом статистичної вибірки й умовами надання кредитів, що змінюються з плином часу. Саме з цієї причини була запропонована ідея розробки нечіткої моделі для оцінювання фінансової заможності клієнтів з метою прийняття рішень про надання довгострокових кредитів. При цьому як нечітка модель використовується система нечіткого виводу з наступними вхідними і вихідними змінними. 5.2 Описання вхідних і вихідних змінних задачі, що розгляндається Змістовна інтерпретація нечіткої моделі припускає вибір і специфікацію вхідних і вихідних змінних відповідної системи нечіткого виводу. При цьому в нечіткій моделі передбачається використовувати 5 вхідних змінних і 1 вихідну змінну. У якості першої вхідної змінної використовується оцінка місця розташування споруджуваного будинку, що безпосередньо оцінює проект споруджуваного будинку, приймаючи до уваги розміщення будинку в тому чи іншому конкретному районі міста чи регіоні передмістя. Очевидно, чим вище ця оцінка, тим більше ліквідним представляється проект у випадку його реалізації на ринку нерухомості. У якості другої вхідної змінної використовується якість передбачуваного виконання опоряджувальних робіт відповідно до архітектурного проекту споруджуваного будинку. Ця змінна вносить додатковий елемент в оцінку вартості споруджуваного будинку. У якості третьої вхідної змінної використовується оцінка активів, що використовується для оцінки майна чи авуарів у випадку неспроможності потенційного клієнта при неповерненні їм узятого кредиту. Дійсно, величина наданого кредиту повинна ґрунтуватися не тільки на урахуванні вартості споруджуваного будинку, але і на власній капіталізації клієнта. У якості четвертої вхідної змінної використовується оцінка доходу потенційного клієнта за винятком фіксованих витрат, яка також використовується у випадку неспроможності потенційного клієнта при неповерненні їм узятого кредиту. Чим вище значення цієї змінної, тим більше успішним є надання кредиту клієнту.
У якості п'ятої вхідної змінної використовується величина підлягаючих сплаті відсотків відповідно до передбачуваного плану виплат по узятому кредиту. Ця змінна зв'язана з терміном надання кредиту і його величиною, дозволяючи об'єднати в собі відповідні характеристики кредиту. Чим вище величина виплат по відсотках, тим більше високими повинні бути значення активів і доходів для позитивного рішення про надання кредиту потенційному клієнту. У якості вихідної змінної використовується оцінка кредитоспроможності, що є основою для ухвалення рішення керівництвом банку по наданню кредиту потенційним клієнтам. При цьому рішення про надання кредиту керівництвом банку приймається тільки у випадку високої оцінки цієї вихідної змінної. Аналіз надання кредитів на будівництво будинків показує, що для аналізу фінансової заможності потенційних клієнтів керівництво банків застосовує наступні евристичні правила: 1. Якщо величина доходу низька і величина виплат середня, то кредитоспроможність дуже низька. 2. Якщо величина доходу низька і величина виплат висока, то кредитоспроможність дуже низька. 3. Якщо величина доходу середня і величина виплат висока, то кредитоспроможність дуже низька. 4. Якщо активи низькі і величина доходу низька, то кредитоспроможність дуже низька. 5. Якщо активи низькі і величина доходу середня, то кредитоспроможність дуже низька. 6. Якщо активи середні і величина доходу низька, то кредитоспроможність дуже низька. 7. Якщо якість опоряджувальних робіт погана, активи низькі і величина доходу висока, то кредитоспроможність дуже низька. 8. Якщо якість опоряджувальних робіт погана, активи середні і величина доходу середня, то кредитоспроможність дуже низька. 9. Якщо якість опоряджувальних робіт погана, активи високі і величина доходу низька, то кредитоспроможність дуже низька. 10. Якщо якість опоряджувальних робіт погана, активи високі і величина доходу середня, то кредитоспроможність дуже низька. 11. Якщо місцезнаходження непрестижне, якість опоряджувальних робіт гарна, активи низькі і величина доходу висока, то кредитоспроможність середня. 12. Якщо місцезнаходження непрестижне, якість опоряджувальних робіт прекрасна, активи низькі і величина доходу висока, то кредитоспроможність середня. 13. Якщо місцезнаходження престижне, якість опоряджувальних робіт гарна, активи низькі і величина доходу висока, то кредитоспроможність середня.
14. Якщо місцезнаходження дуже престижне, якість опоряджувальних робіт гарна, активи низькі і величина доходу висока, то кредитоспроможність середня. 15. Якщо місцезнаходження непрестижне, якість опоряджувальних робіт гарна, активи середні і величина доходу середня, то кредитоспроможність середня. 16. Якщо місцезнаходження непрестижне, якість опоряджувальних робіт прекрасна, активи середні і величина доходу середня, то кредитоспроможність середня. 17. Якщо місцезнаходження престижне, якість опоряджувальних робіт гарна, активи середні і величина доходу середня, то кредитоспроможність середня. 18. Якщо місцезнаходження дуже престижне, якість опоряджувальних робіт гарна, активи середні і величина доходу середня, то кредитоспроможність середня. 19. Якщо місцезнаходження непрестижне, якість опоряджувальних робіт гарна, активи високі і величина доходу низька, то кредитоспроможність середня. 20. Якщо місцезнаходження непрестижне, якість опоряджувальних робіт прекрасна, активи високі і величина доходу низька, то кредитоспроможність середня. 21. Якщо місцезнаходження престижне, якість опоряджувальних робіт гарна, активи високі і величина доходу низька, то кредитоспроможність середня. 22. Якщо місцезнаходження дуже престижне, якість опоряджувальних робіт гарна, активи високі і величина доходу низька, то кредитоспроможність середня. 23. Якщо місцезнаходження непрестижне, якість опоряджувальних робіт гарна, активи високі і величина доходу середня, то кредитоспроможність середня. 24. Якщо місцезнаходження непрестижне, якість опоряджувальних робіт прекрасна, активи високі і величина доходу середня, то кредитоспроможність середня. 25. Якщо місцезнаходження престижне, якість опоряджувальних робіт гарна, активи високі і величина доходу середня, то кредитоспроможність середня. 26. Якщо місцезнаходження дуже престижне, якість опоряджувальних робіт гарна, активи високі і величина доходу середня, то кредитоспроможність середня. 27. Якщо місцезнаходження престижне, якість опоряджувальних робіт прекрасна, активи середні і величина доходу висока, то кредитоспроможність дуже висока. 28. Якщо місцезнаходження престижне, якість опоряджувальних робіт прекрасна, активи високі і величина доходу висока, то кредитоспроможність дуже висока. 29. Якщо місцезнаходження дуже престижне, якість опоряджувальних робіт прекрасна, активи середні і величина доходу висока, то кредитоспроможність дуже висока. 30. Якщо місцезнаходження дуже престижне, якість опоряджувальних робіт прекрасна, активи високі і величина доходу висока, то кредитоспроможність дуже висока. 31. Якщо місцезнаходження непрестижне, якість опоряджувальних робіт гарна, активи середні і величина доходу висока, то кредитоспроможність висока. 32. Якщо місцезнаходження непрестижне, якість опоряджувальних робіт прекрасна, активи середні і величина доходу висока, то кредитоспроможність висока. 33. Якщо місцезнаходження престижне, якість опоряджувальних робіт гарна, активи середні і величина доходу висока, то кредитоспроможність висока.
34. Якщо місцезнаходження дуже престижне, якість опоряджувальних робіт гарна, активи середні і величина доходу висока, то кредитоспроможність висока. 35. Якщо місцезнаходження непрестижне, якість опоряджувальних робіт гарна, активи високі і величина доходу висока, то кредитоспроможність висока. 36. Якщо місцезнаходження непрестижне, якість опоряджувальних робіт прекрасна, активи високі і величина доходу висока, то кредитоспроможність висока. 37. Якщо місцезнаходження престижне, якість опоряджувальних робіт гарна, активи високі і величина доходу висока, то кредитоспроможність висока. 38. Якщо місцезнаходження дуже престижне, якість опоряджувальних робіт гарна, активи високі і величина доходу висока, то кредитоспроможність висока. 39. Якщо місцезнаходження престижне, якість опоряджувальних робіт прекрасна, то кредитоспроможність висока. 40. Якщо місцезнаходження дуже престижне, якість опоряджувальних робіт прекрасна, то кредитоспроможність висока. Після розгляду змістовної постановки задачі можна приступити до побудови ее нечіткої моделі у формі відповідної системи нечіткого виводу. Для цієї мети скористаємося розглянутими раніше графічними засобами пакета Fuzzу Logic Тооlbох системи МАТLАВ.
5.3 Розробка нечіткої моделі оцінювання фінансової заможності клієнтів При побудові нечіткої моделі оцінки фінансової заможності потенційних клієнтів було зроблене припущення про те, що всі розглянуті змінні виміряються в балах в інтервалі дійсних чисел від 0 до 10. При цьому найнижча оцінка значення кожної із змінних є 0, а найвища — 10. Фазифікація вхідних і вихідних змінних Як терм-множину першої вхідної змінної "Місцезнаходження" (Loсаtion) будемо використовувати множину Т1={ "непрестижне", "престижне", "дуже престижне" } або в символічному виді Т1={PS, РМ, РВ}. Як терм-множину другої вхідної змінної "Опоряджування" (Work-manship) будемо використовувати аналогічну множину Т2={ "погане", "гарне", "прекрасне" } або в символічному виді Т2={PS, РМ, РВ}. Як терм-множину третьої лінгвістичної змінної "Активи" (Аsset) будемо використовувати множину Т3={ "низькі", "середні", "високі" } чи в символічному виді Т3={РS, РМ, РВ}. Як терм-множину четвертої лінгвістичної змінної "Доход" (Income) будемо використовувати аналогічну множину T4={ "низький", "середній", "високий" } чи в символічному виді T4={РS, РМ, РВ}. Як терм-множину п'ятої лінгвістичної змінної "Виплати" (Interest) будемо використовувати аналогічну множину T5= { "низькі", "середні", "високі"} чи в символічному виді T5={РS, РМ, РВ}. Як терм-множину вихідної лінгвістичної змінної "Кредитоспроможність" (Сredit) будемо використовувати множину T6={ "дуже низька", "низька", "середня", "висока", "дуже висока" } чи в символічномувиді T6={NВ, NS,Z, РS, РВ}.
5.4 Формування бази правил систем нечіткого виводу Наступним етапом побудови моделі є побудова бази правил. Для цієї мети будемо використовувати 40 правил нечітких продукцій, які зручно представити у виді наступної таблиці 5.1. Таблиця 5.1. Правила нечітких продукций для розглянутої системи нечіткого виводу
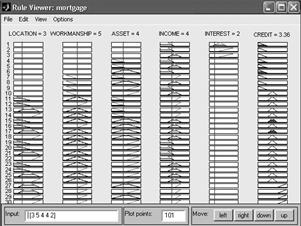
Як схему нечіткого виводу будемо використовувати метод Мамдані, тому методом активації буде МІN. Далі необхідно визначити методи агрегувания підумов. Оскільки у всіх правилах 1 — 40 як логічне зв'язування для підумов застосовується тільки нечітка кон'юнкція (операція "І"), то як метод агрегування будемо використовувати операцію min-кон'юнкції. Для акумуляції виводів правил будемо використовувати метод mах-дизъ'юнкції, що також застосовується у випадку схеми нечіткого виводу методом Мамдані. Нарешті, як метод дефазифікації будемо використовувати метод центра ваги. 5.5 Побудова нечіткої моделі засобами Fuzzу Logic Тооlbох і Розробку нечіткої моделі (назвемо її mortgagе) будемо виконувати з використанням графічних засобів системи МАТLАВ. З цією метою в редакторі FIS визначимо 5 вхідних змінних з іменами "місцезнаходження" (b1), "опоряджування" (b2), "активи" (b3), "доход" (b4), "виплати" (b5) і одну вихідну змінну з ім'ям "кредитоспроможність" (b6). Вид графічного інтерфейсу редактора FIS для цих змінних зображений на рис.5.1. Для вирішення поставленої задачі нечіткого моделювання будемо використовувати систему нечіткого виводу типу Мамдані. Залишимо без зміни параметри розроблювальної нечіткої моделі, запропоновані системою МАТLАВ за замовчуванням, а саме, логічні операції (min — для нечіткого логічного I, mах — для нечіткого логічного ЧИ), метод імплікації (min), метод агрегування (mах) і метод дефазифікації (centroid). Далі варто визначити функції належності термів для кожної з 5 вхідних і єдиної вихідної змінних розглянутої системи нечіткого виводу. Для цієї мети скористаємося редактором функцій належності системи МАТLАВ. Графічний інтерфейс редактора функцій належності для вихідної змінної "кредитоспроможність" зображений на рис.5.2. Далі задамо 40 правил для розроблювальної системи нечіткого виводу (табл. 5.1). Для цієї мети скористаємося редактором правил системи МАТLАВ. Вид графічного інтерфейсу редактора правил після завдання всіх 40 правил нечіткого виводу зображений на рис.5.6. Оскільки в робочому вікні відображаються не всі змінні нечіткої моделі, для керування режимом відображення змінних правил варто скористатися спеціальними кнопками, розташованими в нижній правій частині редактора правил. Тепер можна виконати аналіз побудованої системи нечіткого виводу для розглянутої задачі оцінки фінансової заможності клієнтів. З цією метою відкриємо вікно перегляду правил системи MATLAB і введемо значення вхідних змінних для частинного випадку, коли значення вхідної змінної "місцезнаходження" оцінюється в 8 балів, значення вхідної змінної “опоряджування” також оцінюється в 8 балів, значення вхідної змінної "активи" оцінюється в 9 балів, значення вхідної змінної "доход" оцінюється в 9 балів, і, нарешті, значення вхідної змінної "виплати" оцінюється в 5 балів. Це досить високі оцінки вхідних змінних, котрі навіть на інтуїтивному рівні свідчать на користь відповідного клієнта. Процедура нечіткого виводу, виконана системою MATLAB для розробленої нечіткої моделі, видає в результаті значення вихідної змінної "кредитоспроможність", рівне 7.75 бала (рис.5.4). Це досить висока оцінка фінансової заможності потенційного клієнта, що може служити підставою для позитивного рішення з боку банку про надання кредиту під заставу. Як можна заключити, даний висновок цілком узгоджується з раніше висловленими інтуїтивними розуміннями.
Рис. 5.1. Графічний інтерфейс редактора FIS після визначення вхідних і вихідної змінних системи нечіткого виводу mortgage
Рис. 5.2. Графічний інтерфейс редактора функцій належності для вихідної змінної "кредитоспроможність"
Рис. 5.3. Графічний інтерфейс програми перегляду правил після виконання процедури нечіткого виводу 1 варіанту Ї
Рис. 5.4. Графічний інтерфейс програми перегляду правил після виконання процедури нечіткого виводу 2 варіанту
Далі виконаємо аналіз побудованої системи нечіткого виводу для другого варіанта вихідних даних з більш низькими оцінками значень вхідних змінних. З цією метою змінимо значення вхідних змінних: значення вхідної змінної "місцезнаходження" оцінимо в 3 бали, значення вхідної змінної “опоряджування” оцінимо в 5 балів, значення вхідної змінної "активи" оцінимо в 4 бали, значення вхідної змінної "доход" оцінимо в 4 бали, і, нарешті, значення вхідної змінної "виплати" оцінимо в 2 бали. Процедура нечіткого виводу, виконана системою МАТLАВ, видає в результаті значення вихідної змінної "кредитоспроможність", рівне 3.42 бала. Це досить низька оцінка фінансової заможності потенційного клієнта, що може служити підставою для негативного рішення з боку банку про надання кредиту під заставу. Як можна заключити в цьому випадку, даний висновок також узгоджується з інтуїтивними розуміннями на цей рахунок. Порівняння результатів нечіткого виводу для двох розглянутих варіантів значень вхідних змінних показує, що граничне значення вихідної змінної "кредитоспроможність", що впливає на рішення про надання кредиту, може бути обране в межах 5 балів.
Примітка Для більш тонкого настроювання побудованої нечіткої моделі необхідно доповнити її конкретними методиками бальної оцінки окремих кількісних значень вхідних і вихідних лінгвістичних змінних. Оскільки такі методики в значній мірі залежать від розглянутої проблемної області, від сформованої на даний момент ринкової кон'юнктури і мають приватний характер для конкретного банку, тут вони не розглядаються.
Для загального аналізу розробленої нечіткої моделі також може виявитися корисною візуалізація відповідної поверхні нечіткого виводу (рис.5.5). Дана поверхня нечіткого виводу дозволяє установити залежність значень вихідної змінної від значень окремих вхідних змінних нечіткої моделі. Аналіз цих залежностей може служити підставою для зміни функцій належності вхідних змінних чи нечітких правил з метою підвищення адекватності системи нечіткого виводу для конкретних стратегій банків.
Рис. 5.5. Візуалізація поверхні нечіткого виводу розглянутої моделі для вхідних змінних "місцезнаходження" і "обробка" Слід зазначити також ту обставину, що розроблювачі даної нечіткої моделі відзначають її декілька спрощений характер у порівнянні з реально використовуваною в процесі прийняття рішень керівництвом банку. У той же час розглянута нечітка модель має досить високу адекватність, що обумовлює її успішне застосування в практиці фінансових операцій деяких банків. Таблиця 5.2 Встановлення ваги правил
Лабораторна робота №5 Розробка систем АНАЛІЗУ ДАНИХ методами Мета роботи: Освоїти методику проектування і побудови систем інтелектуального аналізу даних на основі методів нечіткої кластеризації. Основні поняття Кластерний аналіз – це сукупність методів, підходів і процедур, які розробляються для розв’язування проблеми формування класів – сукупностей даних, однорідних за заданими ознаками. Кластерний аналіз (автоматична класифікація сукупності даних) займає одно з центральних місць серед методів аналізу даних і являє собою сукупність підходів та алгоритмів знаходження деякого розбиття досліджуваної сукупності об’єктів на підмножини відносно схожих між собою елементів. Такі підмножини отримали назву кластерів. Виділення кластерів серед сукупності даних має відповідати наступним вимогам: 1. кожний кластер представляє собою сукупність об’єктів, які схожі між собою значеннями деяких властивостей або ознак; 2. сукупність всіх кластерів має бути вичерпаною, тобто всі об’єкти досліджуваної сукупності мають належить до деякого кластеру; 3. кластери мають бути взаємно-виключні; тобто, жоден з об’єктів не має належить до двох різних кластерів. Формально, під задачею кластерного аналізу розуміється задача знаходження деякого теоретико-множинного розбиття початкової множити об’єктів на підмножини, які не перетинаються, таким чином, щоб елементи, які відносяться до однієї підмножини відрізнялися між собою в значно меншій степені, ніж об’єкти з різних підмножин. Концептуальний зв'язок між кластер ним аналізом і теорією нечітких множин оснований на тому, що при розв’язуванні задач структуризації складних систем більшість класів, що формуються, «розмиті» за своєю природою. Тому, найбільш адекватну відповідь слід шукати не на питання «Чи належить елемент до того чи іншого класу?», а на питання «В якій степені даний елемент належить класу, що розглядається?». Методи нечіткої кластеризації вводять до розгляду нечіткі кластери і відповідні їм функції належності, які приймають значення з інтервалу Таким чином, задача нечіткої кластеризації полягає у тому, що необхідно знайти нечітке розбиття або нечітке покриття множини елементів сукупності, що досліджується. Задача зводиться до знаходження степенем належності елементів множини нечітким кластерам (класам). Постановка задачі Нехай початкова (досліджувана) сукупність даних представляє собою скінчену множину елементів Далі, пропонується, що для всіх елементів множини об’єктів кластеризації виміряли всі ознаки множини Р, і кожен елемент множини Взагалі, проблема кількісного вимірювання ознак кожного об’єкта з сукупності – нетривіальна і самостійна задача. Процес вимірювання ознак може бути реалізований в різних шкалах, кожна з яких характеризується допустимим перетворенням даних. В зв’язку з цим, визначають різні типи шкал: - шкала найменувань: об’єкту ставиться у відповідність деякий символ або номер, який лише відокремлює одне значення ознаки від іншого; прикладом таких ознак є стать людини –(м, ж) або найменування міст (Київ, Житомир, Луганськ,...); допустимим відображенням множини об’єктів у множину символів є бієктивне відображення; - порядкова шкала: разом з відповідною множиною символьних ознак об’єктів ця шкала дозволяє встановити відношення порядку відносно цієї ознаки; тоді об’єкту ставиться у відповідність деяке число, яке грає роль його оцінки в балах; допустимим відображенням є монотонне зростаюче відображення або функція між двома множинами значень ознак; приклад – оцінки на іспитах; - інтервальна шкала: крім порядку елементів по ознакам ця шкала встановлює рівність інтервалів значень цієї ознаки; об’єкту, як правило, ставиться у відповідність число, яке дорівнює значенню цієї ознаки; допустимим перетворенням тут є довільна лінійна зростаюча функція між двома множинами значень ознак; характерною ознакою такої шкали є відсутність абсолютного нуля; приклад – температура в шкалах Цельсія; - шкала відношень: в доповнення до рівності інтервалів додає ще рівність відношень значень ознаки, що розглядається; об’єкту ставиться у відповідність деяке число, яке дорівнює значенню цієї ознаки; допустимим відображенням є довільна лінійна зростаюча функція, яка проходить через нуль; приклад – відстань в метрах, швидкість в км/ч. Множину ознак слід обирати таким чином, щоб всі
Вектори значень ознак Отже, задача нечіткого кластерного аналізу формулюється наступним чином: на основі даних матриці D визначити таке нечітке розбиття Для конкретизації задачі ще слід уточнити вигляд цільової функції та тип шуканих нечітких кластерів.
Одним з видів конкретизації цієї задачі є використання спеціальної функції fcm системи MATLAB, який оснований на алгоритмі розв’язування методом нечітких с-середніх. Для уточнення вигляду цільової функції
де с – загальна кількість нечітких кластерів Далі для кожного кластеру вводяться так звані типові представники або центри
де m – деякий параметр, який має назву експоненційна вага і дорівнює деякому дійсному числу (m>1). Кожний з центрів кластерів є вектором В якості цільової функції будемо розглядати суму квадратів зважених відхилень координат об’єктів кластеризації від центрів нечітких кластерів:
Чим більше елементів містить множина А, тим менше значення слід вибирати для m>1. Тоді задача нечіткої кластеризації полягає у наступному: для заданої матриці даних D, кількості нечітких кластерів
Умови (4) виключають появу пустих нечітких кластерів в шуканій нечіткій кластеризації. Таким чином, мінімізація цільової функції (6.3) мінімізує відхилення всіх об’єктів кластеризації від центрів нечітких кластерів пропорційно значенням функцій належності цих об’єктів відповідним нечітким кластерам. Ця функція не є випуклою, а тому задача кластеризації в загальному випадку відноситься до багатоекстремальних задач нелінійного програмування.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 742; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.179.27 (0.019 с.) |







 .
. , яке ще називається множиною об’єктів кластеризації. Вводиться також скінчена множина ознак або атрибутів об’єктів
, яке ще називається множиною об’єктів кластеризації. Вводиться також скінчена множина ознак або атрибутів об’єктів 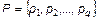 , кожний з яких являє собою деяку характеристику елементів множини
, кожний з яких являє собою деяку характеристику елементів множини  .
. представлений вектором
представлений вектором  , де
, де  - дійсне значення ознаки
- дійсне значення ознаки  для об’єкту
для об’єкту 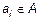 .
.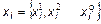 зручно представляти у вигляді матриці даних D розмірності (n*q), кожний рядок якої представляє собою значення вектору
зручно представляти у вигляді матриці даних D розмірності (n*q), кожний рядок якої представляє собою значення вектору  .
. або нечітке покриття
або нечітке покриття 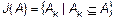 множини А на задане число нечітких кластерів
множини А на задане число нечітких кластерів  , яке доставляє екстремум деякій цільовій функції
, яке доставляє екстремум деякій цільовій функції 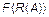 серед всіх нечітких розбиттів чи екстремум цільової функції
серед всіх нечітких розбиттів чи екстремум цільової функції 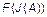 серед всіх можливих нечітких покриттів.
серед всіх можливих нечітких покриттів. , (6.1)
, (6.1) шуканих нечітких кластерів
шуканих нечітких кластерів  , (6.2)
, (6.2) в деякому q-вимірному нормованому просторі ознак, який ізоморфний
в деякому q-вимірному нормованому просторі ознак, який ізоморфний  , якщо всі ознаки виміряні по шкалі відношень.
, якщо всі ознаки виміряні по шкалі відношень. . (6.3)
. (6.3) , параметра m, визначити матрицю U значень функції належності об’єктів кластерізації
, параметра m, визначити матрицю U значень функції належності об’єктів кластерізації  (6.4).
(6.4).


