
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Фреймові системи представлення знаньСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Фреймові моделі (системи, мережі фреймів) у порівнянні із семантичними мережами дають більш формалізований і в той же час досить гнучкий «механізм» представлення знань. Випереджаючи строге визначення фрейму, помітимо, що фрейм можна розглядати як складний вузол в особливого виду семантичної мережі. У рамках фреймових моделей вдалося значною мірою об'єднати декларативні знання про об'єкти і процедурні знання про методи витягу і перетворення інформації для досягнення заданих цілей. Термін фрейм (каркас, рамка) був запропонований у 1973р. М Мінським для мінімального опису явищ, понять, об'єктів. Відповідно до його визначення фрейми – це структури даних (знань), використовувані для представлення стереотипних ситуацій. У психології та філософії відоме поняття абстрактного образа чи прототипу. Наприклад, при проголошенні вголос слова «кімната» виникає її абстрактний образ (рамка чи фрейм), що включає житлове приміщення з чотирма стінами, підлогою, стелею, вікнами і дверима, площею від (приблизно) 6 до 20 кв.м. Цей опис мінімальний в тому розумінні, що з нього нічого не можна забрати. Так, забравши вікна, одержимо фрейм прикомірки чи комори і т.п. У цьому мінімальному описі опущені деталі (колір стін, кількість вікон і т.д.) Факт існування подібних деталей для конкретної кімнати враховується тим, що в згаданому описі маються слоти – вакантні клітини пам’яті. На рівні мінімального опису кімнати як прототипу деякого житлового приміщення ці слоти не заповнені. Вони заповнюються (чи прототип обрамляється) конкретними значеннями атрибутів кімнати (кількість вікон, колір стін, висота стель і ін.), якщо має місце деяка конкретна ситуація. Абстрактний образ (прототип) деякого об'єкта з потенційною можливістю його обрамлення атрибутами називається фреймом. Він дозволяє сконцентрувати всі знання про даний об'єкт (чи клас об'єктів) у єдиній структурі даних (фреймі), а не розпорошувати їх між безліччю більш дрібних структур начебто логічних формул чи продукцій. Декларативні і процедурні знання про деяку сутність укладаються (пакуються) у єдину структуру (фрейм). Інформаційна структура фрейму представлена на рис.1.Фрейм складається з імені, що виконує роль ідентифікатора, і слотів. Ідентифікатор, що привласнюється фрейму, повинний мати унікальне ім'я, єдине в даній фреймовій (мережній) системі. Кожен фрейм включає довільне число слотів, при цьому деякі з них визначаються самою системою, а інші задаються користувачем. Кожен слот має визначену структуру даних, що включає: · Ім'я слота. Це ідентифікатор, що привласнюється слоту. Він унікальний у межах даного фрейму.
Ім'я фрейму
Рис.1.2 Структура фрейму
· Ім'я атрибута слота – ідентифікатор атрибута слота. · Значення (атрибута) слота (приєднана процедура). Покажчики типу даних атрибутів, значення атрибутів. Особливістю є наявність у слоті так званих приєднаних (інкапсульованих) процедур. Приєднана процедура являє собою програму процедурного типу, що запускається за повідомленнями, які одержані з інших фреймів. · Демон. Демоном називається процедура, яка автоматично запускається при виконанні деякої умови. Наприклад, демон IF-NEEDED запускається, якщо в момент звертання до слоту його значення не було встановлено. Демон IF-ADDED запускається при підстановці в слот значення, демон IF-REMOVED – при стиранні значення слота. У результаті виконуються всі рутинні операції, що забезпечують підтримку бази знань в актуальному стані. Завдяки слотам-посиланням (“a kind of”, “is a”, та ін) фреймові системи утворять ієрархічні структури, що реалізують принцип спадкування інформації. Спадкування відбувається в напрямку «суперклас-підклас», «клас-екземпляр класу». Фрейм, у якому заповнені всі значення слотів, називається фреймом - екземпляром. Існують ще зразки чи фрейми-прототипи. Вони являють собою оболонку, у якій зазначені тільки імена слотів. Інкапсульовані в слоти чи приєднані процедури є важливою особливістю фреймових мереж, що істотно відрізняють їх від мереж семантичних. Ці процедури додають фреймовій системі можливість керування виводом, таким же способом, як це робиться на основі використання об’єктно-орієнтованих мов.
§2. Лабораторна робота №1 ПРОЕКТУВАННЯ СИСТЕМ НЕЧІТКОГО ВИВОДУ НА ОСНОВІ Мета роботи: освоїти методику проектування системи нечіткого виводу на основі розробки та використання баз знань продукційних правил з використанням алгоритму Мамдані. Основні поняття Знання можна формалізувати у вигляді системи нечітких логічних висловлювань. Кожне висловлювання можна оцінити нечітким ступенем істинності. Наприклад, висловлювання «швидкість машини висока» може бути істинне на 80%, а висловлювання «завтра буде морозна погода» - на 100%. Кожне таке висловлювання можна описати за допомогою відношень множин лінгвістичних нечітких змінних. Лінгвістична змінна – це кортеж наступних значень
T – базова множина значень її термів – значень, кожне з яких надається за допомогою нечіткої множини (наприклад, «мала», «середня», «висока», «дуже висока»); X – множина – носій можливих конкретних значень змінної для всіх термів (наприклад,
М – семантична процедура надання терму певної нечіткої змінної вигляду В системі MATLAB існує середовище для формування систем знань нечіткого виводу. Для входу в це середовище слід ввести в командному рядку слово fuzzy і натиснути клавішу <Enter>. Побудова системи нечіткого виводу (СНВ), яка основана на використанні алгоритму Мамдані, має наступні етапи: 1. Проектування бази правил СНВ. Кожне правило представляється у вигляді: Якщо <умова> тоді <заключення> [міра вірності правила]
Для алгоритму Мамдані <умова> і <заключення> виглядають як логічні зв’язки наступних записів: <нечітка змінна> = < значення > 2. Введення цих правил в СНВ 3. Використання СНВ для обробки вхідної інформації у вигляді конкретних значень вхідних (нечітких) змінних. Цей етап, в свою чергу, розкладається на наступні складові: 3.1 Введення значень вхідних змінних. Тобто, деякий фактів, які вважаються істинні на 100%. 3.2 Фазифікація вхідних змінних – встановлення відповідності між конкретним значенням вхідних змінних і значенням її терму, разом з функцією належності 3.3 Агрегування складних умов, які стоять в правилах після ключового слова ЯКЩО, тобто визначення степені істинності всіх умов в усіх правилах, якщо умови надаються за допомогою складних логічних виразів. Правило активується, якщо істинність його умови більша за нуль. В базах знань процедура агрегування умов в правилах виконується за допомогою нечітких логічних операцій – нечіткої кон’юнкції, нечіткої діз’юнкції, нечіткої відмови, та ін. 3.4 Активація підзаключень – процес визначення степені істинності (належності до відповідних термів) змінних, які стоять в заключеннях активних правил, за формулою:
· min – активізація: · prod-активізація: · average-активізація: Відзначимо, що різні правила підзаключень можуть містити однакові терми лінгвістичних змінних. У цьому випадку для кожного терму ми визначаємо множину різних функцій належності, які обчислюються за одним із правил нечіткої композиції по кожному правилу продукцій. Остаточна функція належності для цього терму визначається у наступному пункті. 3.5 Акумуляція заключень, тобто, визначення значення функцій належності для термів всіх вихідних змінних. Якщо для одного терму визначена множина функцій належності
· об’єднання: · алгебраїчне об’єднання: · граничне об’єднання: · операція · драстичне об’єднання:
3.6 Дефазифікація вихідних змінних (визначення конкретних значень за функціями належності термів) розглядається методом центру ваги для неперервних та дискретних нечітких множин за формулами:
Розглянемо принципи побудови та роботи системи нечіткого виводу на прикладі задачі візуалізації поверхні, яка задана функцією.
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 824; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.007 с.) |

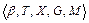 , де
, де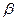 - ім’я змінної (наприклад, «швидкість автомобіля»);
- ім’я змінної (наприклад, «швидкість автомобіля»);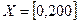 км/год.);
км/год.);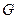 - деяка синтетична процедура генерації нових термів з множини Т (наприклад, «дуже мала»);
- деяка синтетична процедура генерації нових термів з множини Т (наприклад, «дуже мала»);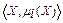 ,
, 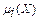 - функція належності і -того терму з множини Т.
- функція належності і -того терму з множини Т.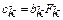 , де
, де 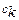 - степінь істинності заключення правила k,
- степінь істинності заключення правила k, 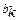 - степінь істинності його умови,
- степінь істинності його умови, 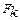 - степінь істинності самого правила (ваговий коефіцієнт
- степінь істинності самого правила (ваговий коефіцієнт 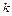 -правила). Після визначення вектору
-правила). Після визначення вектору 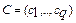 визначаються функції належності для кожного із підзаключень для кожної вихідної лінгвістичної змінної. Припустимо, що відповідний терм вихідної лінгвістичної змінної визначається функцією належності
визначаються функції належності для кожного із підзаключень для кожної вихідної лінгвістичної змінної. Припустимо, що відповідний терм вихідної лінгвістичної змінної визначається функцією належності 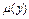 . Тоді після процедури активації отримуємо поновлену функцію належності відповідного терму (підзаключення)
. Тоді після процедури активації отримуємо поновлену функцію належності відповідного терму (підзаключення) 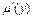 за одним із методів нечіткої композиції:
за одним із методів нечіткої композиції: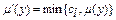 ;
;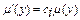 ;
;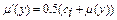 .
.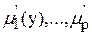 , то акумуляція виконується за одним із правил об’єднання нечітких множин:
, то акумуляція виконується за одним із правил об’єднання нечітких множин: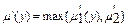 ;
;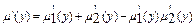 ;
;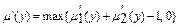 ;
;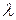 - суми:
- суми: 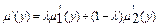 ,
, 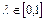 .
.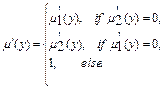
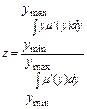 ,
, 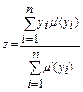 .
.


