Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Графіка і візуалізація данихСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
MatLab володіє широким набором засобів для побудови графіків функцій одній і два змінних і відображення різних типів даних. Всі графіки виводяться в графічні вікна з своїми меню і панелями інструментів. Вид графіків визначається аргументами графічних команд і потім може бути змінений за допомогою інструментів графічного вікна. Важливо розуміти, що для побудови графіків функцій на деякій області зміни аргументів слід обчислити значення функції в точках області, часто для отримання хороших графіків слід використовувати достатньо багато точок. Розберемо спочатку, як отримати графік функції однієї змінної, наприклад:
на відрізку [-2,2]. Для побудови графіка функції використовується одна з графічних функцій MatLab. Достатньо універсальною графічною функцією є plot. У найпростішому випадку вона викликається з двома вхідними аргументами — парою x і f (т. е. plot виводить залежність елементів одного вектора від елементів іншого). Послідовність команд, записана нижче, приводить до появи графічного вікна Figure No.1 з графіком функції. >> x=[-2:0.05:2]; >> f=exp(x).*sin(pi*x)+x.^2; >> plot(x,f) Тип лінії, колір і маркери визначаються значенням третього додаткового аргументу функції plot. Цей аргумент вказується в апострофах, наприклад, виклик plot(x,f,'ro:') призводить до побудови графіка червоною пунктирною лінією, розміченою круглими маркерами. Звернете увагу, що абсциси маркерів визначаються значеннями елементів вектора x. Всього в додатковому аргументі може бути заповнена три позиції, відповідні квітну, типу маркерів і стилю лінії. Позначення для них приведені в табл. 4.1. Порядок позицій може бути довільний, допустимо вказувати тільки один або два параметри, наприклад, колір і тип маркерів. Подивіться на результат виконання наступних команд: plot(x,f,'g'), plot(x,f,'ko'), plot(x,f,':'). Функція plot має достатньо універсальний інтерфейс, вона, зокрема, дозволяє відображати графіки декількох функцій на одних осях. Нехай потрібно вивести графік не тільки f (x), але і на відрізку [-2, 2]. Спочатку необхідно обчислити значення g(x): >> g=exp(-х.^2).*sin(5*pi*x); а потім викликати plot, вказавши через кому пари x, f і x, g і, при бажанні, властивості кожній з ліній: >> plot(x,f,'ko-', x,g,'k:') Таблиця Д4.1 Скорочення для кольору, типу маркерів і стилю ліній
Допускається побудова довільного числа графіків функцій, властивості всіх ліній можуть бути різними. Крім того, області побудови кожною з функцій не обов'язково повинні збігатися, але тоді слід використовувати різних вектора для значень аргументів і обчислювати значення функцій від відповідних векторів. Для отримання графіка шматково-заданої функції:
досить виконати послідовність команд: >> x1=[-4*pi:pi/10:-pi]; >> y1=sin(x1); >> x2=[-pi:pi/30:0]; >> y2=3*(x2/pi+1).^2; >> x3=[0:0.02:5]; >> y3=3*exp(-x3) >> plot(x1,y1,x2,y2,x3,y3) Зауважте, що графіки гілок функції відображаються різними кольорами. Можна було поступити і по-іншому, а саме: після заповнення x1, y1, x2, y2, x3 і y3 зібрати вектор x для значень аргументу і вектор для значень y(x) і побудувати залежність від x: >> x=[x1 x2 x3]; >> y=[y1 y2 y3]; >> plot(x,y) Нескладно здогадатися, як побудувати графік параметрично заданої функції, використовуючи ту обставину, що plot відображає залежність одного вектора від іншого. Нехай потрібно отримати графік астроїди: >> t=[0:pi/20:2*pi]; >> x=cos(t).^3; >> y=sin(t).^3; >> plot(x,y) Функція comet дозволяє простежити за рухом точки по траєкторії параметрично заданої лінії. Виклик comet(x,y) наводить до появи графічного вікна, на осях якого малюється переміщення точки у вигляді руху комети з хвостом. Управління швидкістю руху здійснюється зміною кроку при визначенні вектора значень параметра. У MatLab є графічні функції, призначені для відображення графіків в логарифмічному і напівлогарифмічному масштабах: · Loglog (логарифмічний масштаб по обох осях); · Semilogx (логарифмічний масштаб тільки по осі абсцис); · Semilogy (логарифмічний масштаб тільки по осі ординат).
Вхідні аргументи цих функцій задаються так само, як і при використанні plot. Для порівняння поведінки двох функцій із значеннями різних порядків зручно застосовувати plotyy. Функція plotyy викликається від двох пар вхідних аргументів (векторів) і приводить до появи двох ліній графіків, кожною з яких відповідає своя вісь ординат. Графіки оформляються в MatLab спеціальними командами і функціями. Сітка наноситься на осі командою grid on, а забирається за допомогою grid off. Заголовок розміщується в графічному вікні за допомогою функції title, вхідним аргументом якої являється рядок, ув’язнена в апострофи: >> title('Результати експерименту') За наявності декількох графіків потрібно розташувати легенду звернувшись до legend. Надписи, легенди, ув’язнені, в апострофи вказуються у вхідних аргументах функції legend, їх число повинне співпадати з числом ліній графіків. Крім того, останній додатковий вхідний аргумент визначає положення легенди: –1 — поза графіком в правому верхньому кутку графічного вікна; 0 — вибирається краще положення в межах графіка так, щоб якомога менше перекривати самі графіки; 1 — у верхньому правому кутку графіка (це положення використовується за умовчанням); 2 — у верхньому лівому кутку графіка; 3 — в нижньому лівому кутку графіка; 4 — в нижньому правому кутку графіка. Функції xlabel і ylabel призначені для підписів до осей, їх вхідні аргументи так само полягають в апострофи. Звернемося тепер до візуалізації векторних і матричних даних. Найпростіший спосіб відображення векторних даних полягає у використанні функції plot з вектором як вхідний аргумент. При цьому графік, що виходить у вигляді ламаної лінії, символізує залежність значень елементів вектора від їх індексів. Другий додатковий аргумент може визначати колір, стиль лінії і тип маркерів, наприклад: plot(x,'ko'). Виклик функції plot від матриці приводить до декількох графіків, їх число співпадає з числом стовпців матриці, а кожний з них є залежністю елементів стовпця від їх рядкових індексів. Колір і стиль ліній і тип маркерів відразу для всіх ліній так само визначається другим додатковим аргументом. Наглядним способом представлення матричних і векторних даних є різноманітні діаграми. Проста стовпцева діаграма будується за допомогою функції bar: >> x=[0.7 2.1 2.5 1.9 0.8 1.3]; >> bar(x) Додатковий числовий аргумент bar указує на ширину стовпців (за умовчанням він рівний 0.8), а значення великі одиниці, наприклад bar(x,1.2), приводять до часткового перекриття стовпців. Вказівка матриці у вхідному аргументі bar приводить до побудови групової діаграми, число груп співпадає з числом рядків матриці, а усередині кожної групи стовпчиками відображаються значення елементів рядків. Кругові діаграми векторних даних виходять за допомогою функції pie, яка має деякі особливості в порівнянні з bar. Розрізняються два випадки: 1. якщо сума елементів вектора більше або рівна одиниці, то виводиться повна кругова діаграма, площа кожного її сектора пропорційна величині елементу вектора; 2. якщо сума елементів вектора менше одиниці, то результатом є неповна кругова діаграма, в якій площа кожного сектора пропорційна величині елементів вектора, в припущенні що площа всього круга рівна одиниці. Порівняєте, наприклад pie([0.1 0.2 0.3]) і pie([1 2 3]). Можна відокремити деякі сектори від всього круга діаграми, для чого слід викликати pie з другим аргументом — вектором тієї ж довжини, що і вихідний. Ненульові елементи другого вектора відповідають відокремлюваним секторам. Наступний приклад показує, як відокремити від діаграми сектор, відповідний найбільшому елементу вектора x:
>> x=[0.3 2 1.4 0.5 0.9]; >> [m,k]=max(x); >> v=zeros(size(x)); >> v(k)=1; >> pie(x,v) Підписи до секторів діаграми указуються в другому додатковому вхідному аргументі, який полягає у фігурні дужки: >> pie([2400 3450 1800 5100],{'Март','Апрель','Май','Июнь'}) Функції bar і pie мають аналоги: · barh — побудова стовпцевої діаграми з горизонтальним розташуванням стовпців; · bar3, pie3 — побудова об'ємних діаграм. При обробці великих масивів векторних даних часто потрібно отримати інформацію про те, яка частина даних знаходиться в тому або іншому інтервалі. Функція hist призначена для відображення гістограми даних і знаходження числа даних в інтервалах. Вхідним аргументом hist являється вектор з даними, а вихідним — вектор, що містить кількість елементів, що потрапили в кожний з інтервалів. За умовчанням береться десять рівних інтервалів. Наприклад, виклик hist(randn(1,5000)) наводить до появи на екрані гістограми даних, розподілених по нормальному закону, а n=hist(randn(1,5000)) до заповнення вектора n довжини десять (при цьому гістограма не будується). Число інтервалів указується в другому додатковому аргументі hist. Можна задати інтервали, використавши як другий аргумент не число, а вектор, що містить центри інтервалів. Зручніше задавати інтервали не центрами, а межами. В цьому випадку потрібно спочатку визначити кількість елементів в інтервалах за допомогою функції histc, а потім застосувати bar із спеціальним аргументом 'histc', наприклад: >> x=randn(1,10000); >> int=[-2:0.5:2]; >> n=histc(x,int); >> bar(int,n,'histc') Візуалізація функцій два змінних в MatLab може бути здійснена декількома способами, але всі вони припускають однотипні попередні дії. Розглянемо тут тільки побудову графіків функцій два змінних на прямокутній області визначення. Припустимо, що потрібно отримати поверхню функції >> [X,Y]=meshgrid(-1:0.1:1,0:0.1:2); Матриця X складається з однакових рядків, рівних першому вхідному аргументу вектору в meshgrid, а матриця Y — з однакових стовпців, співпадаючих з другим вектором в meshgrid. Такі матриці виявляються необхідними на другому кроці при заповненні матриці Z, кожен елемент якої є значенням функції z ( x,y ) в точках сітки. Нескладно зрозуміти, що використання по-елементних операцій при обчисленні функції z ( x,y ) приводить до необхідної матриці:
>> Z=exp(-X).*sin(pi*Y); Для побудови графіка z (x,y) залишилося викликати відповідну графічну функцію, наприклад: >> mesh(X,Y,Z) На екрані з'являється графічне вікно, що містить каркасну поверхню досліджуваної функції (рис. Д4.1). Звернете увагу, що колір поверхні відповідає значенню функції.
Рис. Д4.1. Приклад графічного вікна
Команда colorbar приводить до відображення в графічному вікні стовпчика, що показує співвідношення між кольором і значенням z (x,y). Колірні палітри графіка можна змінювати, користуючись функцією colormap, наприклад colormap(gray) відображає графік у відтінках сірого кольору. Деякі колірні палітри приведені нижче: · bone — схожа на палітру gray, але з легким відтінком синього кольору; · colorcube — кожен колір змінюється від темного до яскравого; · cool — відтінки блакитного і пурпурного кольорів; · copper — відтінки мідного кольору; · hot плавна зміна: чорний –червоний –оранжевий –жовтий –білий; · hsv — плавна зміна (як барви веселки); · jet плавна зміна: синій –голубий –зелений –жовтий – червоний; · spring — відтінки пурпурного і жовтого; · summer — відтінки зеленого і жовтого; · winter — відтінки синього і зеленого; MatLab надає цілий набір графічних функцій для візуалізації функцій два змінних, серед них:
Зупинимося докладніше на декількох питаннях. Перший з них: як змінювати установки, визначені за умовчанням, при відображенні функцій лініями рівня за допомогою contour, contourf і contour3. Число ліній рівня задається в четвертому додатковому аргументі, наприклад: >> contourf(X,Y,Z,10) Замість числа ліній рівня можна вказати у векторі ті значення z (x,y), для яких потрібно побудувати лінії рівня: >> contour(X,Y,Z[-0.51 -0.25 -0.01 0.89]) Дещо складніше нанести підписи з відповідним значенням z (x,y) до кожної лінії рівня. Для цього доведеться викликати contour з двома вихідними аргументами, перший з них — матриця з інформацією про положення ліній рівня, а другою — вектор з покажчиками на лінії. Отримані змінні слід використовувати як вхідні аргументи функції clabel: >> [CMatr, h] = contour(X, Y, Z[-0.51 -0.25 -0.01 0.89]); >> clabel(CMatr, h) Залиті кольором каркасні поверхні, побудовані за допомогою sufr і surfc, мають постійний колір в межах кожної комірки. Команда shading interp, що викликається після surf і surfc, служить для плавної зміни кольору в межах комірок і приховання ліній сітки на поверхні. Якщо бажано прибрати сітку і зберегти постійний колір комірок, то досить використовувати shading flat, а shading faceted надає графіку колишній вигляд.
Графічні функції за умовчанням розташовують поверхню так, що спостерігач бачить її частину під деяким кутом, а інша — прихована від погляду. Положення спостерігача визначається двома кутами: азимутом (AZ) і кутом піднесення (EL). Азимут відлічується від осі, протилежної y, а кут піднесення — від площини xy. Оглянути поверхню з усіх боків дозволяє функція view. Виклик функції view з двома вихідними аргументами і без вхідних дає можливість визначити поточне положення спостерігача (кути виводяться в градусах): >> [AZ, EL]=view AZ = -37.5000 EL = Ці значення MatLab використовує за умовчанням при побудові тривимірних графіків. Для завдання положення спостерігача слід вказати азимут і кут піднесення (у градусах) як вхідні аргументи view, наприклад: view(0,90) показує вигляд на графік зверху. Перед поворотом графіка доцільно розставити позначення до осей, використовуючи, як і для двовимірних графіків xlabel і ylabel, і zlabel для підпису до вертикальної осі. Функція view допускає ще декілька варіантів виклику: · view(3) — повернення до стандартних установок; · view([x,y,z]) — розміщення спостерігача в точку із координатами x, y і z. Освітлена поверхня будується за допомогою функції surfl, яка дозволяє отримати наглядне уявлення про поведінку досліджуваної функції. Слід врахувати, що краще поєднувати виклик surfl з командою shading interp і колірною палітрою, що містить велику кількість відтінків (gray, copper, bone, winter і т. д.), оскільки поверхня володіє властивостями розсіювання, віддзеркалення і поглинання світла, витікаючого від деякого джерела. Положення джерела можна задавати в четвертому додатковому аргументі surfl, причому або вектором з двох елементів (азимут і кут положення джерела), або вектором з трьох елементів (положення джерела світла в системі координат осей), наприклад: surfl(X,Y,Z[20 80]) або surfl(X,Y,Z[6 8 11]). Розберемо тепер роботу з декількома графіками. Перший виклик будь-якої графічної функції призводити до появи на екрані графічного вікна Figure No. 1, що містить осі з графіком. Проте, при подальших зверненнях до графічних функцій колишній графік пропадає, а новий виводиться в теж саме вікно. Команда figure призначена для створення порожнього графічного вікна. Якщо потрібно отримати декілька графіків в різних вікнах, то перед викликом графічних функцій слід удаватися до figure. Графічні вікна при цьому нумеруються так: Figure No. 2, Figure No. 3 і т. д. Кожне вікно має свої осі, за наявності декількох пар осей (у одному вікні або в різних) виведення графіків проводиться в поточні осі. Остання створена пара осей є поточною. Для того, щоб вибрати поточні осі з декількох що є, досить клацнути по ним лівою кнопкою миші перед викликом графічної функції. Можлива і зворотна ситуація, коли в процесі роботи потрібно додавати графіки що вже є на деяких осях. У цій ситуації перед додаванням графіка слід виконати команду hold on. Для завершення такого режиму досить скористатися hold off. У одному графічному вікні можна розташувати декілька осей з своїми графіками. Функція subplot призначена для розбиття вікна на частини і визначення поточною з них. Припустимо, що потрібно вивести графіки на шість пар осей в одне графічне вікно (дві по вертикалі і три по горизонталі). Створіть графічне вікно за допомогою figure і виконайте команду: >> subplot(2,3,1) У лівому верхньому кутку вікна з'явилися осі. Перші два аргументи в subplot вказують на загальне число пар осей по вертикалі і горизонталі, а останній аргумент означає номер даної пари осей. Нумерація йде зліва направо, зверху вниз. Використовуйте subplot(2,3,2)., subplot(2,3,6) для створення решти пар осей. Висновок будь-якою з графічних функцій можна направити в потрібні осі, вказавши їх за допомогою subplot(2,3,k), наприклад: >> subplot(2,3,3) >> bar([1.2 0.3 2.8 0.9]) >> subplot(2,3,6) >> surf(X,Y,Z) Завдання для самостійної роботи 1. Побудувати графіки функцій однієї змінної на вказаних інтервалах. Вивести графіки різними способами: · у окремі графічні вікна; · у одне вікно на одні осі; · у одне вікно на окремі осі. Дати заголовки, розмістити підписи до осей, легенду, використовувати різні кольори, стилі ліній і типи маркерів, нанести сітку. Варіанти 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 2. Побудувати графіки шматково-заданої функції, відобразити галузь різними кольорами і маркерами.
1.
3. 5. 6. 8. 10.
3. Побудувати графік параметрично заданої функції, використовуючи plot і comet. Варіанти 1. 2. 3. 4. 5. 6. 7. 8. 9. 10.
4. Віалізувати функцію два змінних на прямокутній області визначення різними способами: · каркасною поверхнею; · залитою кольором каркасною поверхнею; · промаркованими лініями рівня (самостійно вибрати значення функції, що відображеними лініями рівня); · освітленою поверхнею. Розташувати графіки в окремих графічних вікнах, і в одному вікні із відповідним числом пар осей. Представити вид каркасної або освітленої поверхні з декількох точок огляду. Варіанти 1. 2. 3. 4. 5. 6. 7. 8. 9. 10.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 443; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.106.87 (0.015 с.) |

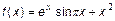

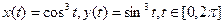 . Слід задати вектор t, потім у вектори X, Y занести значення x(t), y (t) і скористатися plot для відображення залежності Y від X:
. Слід задати вектор t, потім у вектори X, Y занести значення x(t), y (t) і скористатися plot для відображення залежності Y від X: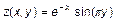 на прямокутнику
на прямокутнику 
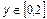 . Перший крок полягає в завданні сітки на прямокутнику, т. е. крапок, які використовуватимуться для обчислення значень функції. Для генерації сітки передбачена функція meshgrid, що викликається від двох вхідних аргументів — векторів, задаючи розбиття по осях x і y. Функція meshgrid повертає два вихідних аргументу, що є матрицями.
. Перший крок полягає в завданні сітки на прямокутнику, т. е. крапок, які використовуватимуться для обчислення значень функції. Для генерації сітки передбачена функція meshgrid, що викликається від двох вхідних аргументів — векторів, задаючи розбиття по осях x і y. Функція meshgrid повертає два вихідних аргументу, що є матрицями.
 .
.  .
.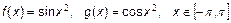 .
.  .
. .
.  .
. .
.  .
.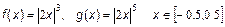 .
.  .
.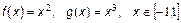 .
.  .
. .
.  .
.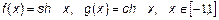 .
.  .
.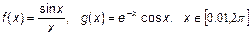 .
.  .
. .
.  .
. 2.
2. 
 4.
4. 

 7.
7. 
 9.
9.