
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проектування систем нечіткого виводу СугеноСодержание книги
Поиск на нашем сайте
Мета роботи: освоїти методику проектування системи нечіткого виводу на основі розробки та використання баз знань продукційних правил з використанням алгоритму Сугено. Провести порівняльний аналіз алгоритмів Мамдані і Сугено.
3.1 Основні поняття Розглянемо основні етапи проектування систем нечіткого виводу за алгоритмом Сугено на прикладі задачі візуалізації поверхні, яка реалізує залежність
Правило <#>: Якщо «змінна 1=значення А» і «змінна 2=В» Тоді «
або
Правило <#>: Якщо «змінна 1 = значення А» і «змінна 2 = В» Тоді «
3.2 Метод проектування та використання систем Моделювання заданої поверхні будемо реалізовувати за допомогою наступних правил бази знань: 1. Якщо х1 та х2 низькі, тоді 2. Якщо х1 низьке, тоді 3. Якщо х1 низьке і х2 вище середнього, тоді 4. Якщо х1 та х2 високі, тоді 5. Якщо х2 низьке, тоді 6. Якщо х1 високе, тоді 7. Якщо х2 високе, тоді 8. Якщо х1 низьке і х2 високе, тоді 9. Якщо х1 середнє і х2 середнє, тоді 10. Тоді проектування системи нечіткого виводу типу Сугено лежить у виконанні наступної послідовності кроків. Крок 1. Для завантаження основного fis-редактору надрукуємо слово fuzzy у командному рядку Mathlab. Крок 2. Оберемо тип системи. Для цього в меню File в підменю New fis… оберемо команду Sugeno. Крок 3. Додамо другу вхідну змінну. Для цього в меню Edit оберемо команду Add input. Крок 4. Перейменуємо першу вхідну змінну. Для цього зробимо одне натиснення лівої кнопки миші на блоці input1, введемо нове позначення x1 в полі редагування імені поточної змінної і натиснемо <Enter>. Крок 5. Перейменуємо другу вхідну змінну. Для цього зробимо одне натиснення лівою кнопкою миші на блоці input2, введемо нове позначення x2 в полі редагування імені поточної змінної і натиснемо <Enter>. Крок 6. Перейменуємо вихідну змінну. Для цього зробимо одне натиснення лівою кнопкою миші на блоці output1, введемо нове позначення y в полі редагування імені поточної змінної і натиснемо <Enter>. Крок 7. Задамо ім’я системи. Для цього в меню File в підменю Export оберемо команду To disk і введемо імя файла, наприклад, FirstSugeno.
Крок 8. Перейдемо в редактор функций належності. Для цього зробимо швидке подвійне натиснення лівої кнопки миші на блоці x1. Крок 9. Зададимо діапазон змін змінної x1. Для цього надрукуємо 0 4 в полі Range і натиснемо <Enter> (див. рис.3.1). Крок 10. Задамо функції належності змінної Крок 11. Аналогічно з адамо функції належності змінної
Рис 3.1. Функції належності змінної Крок 12. Задамо лінійні залежності між входами і виходом, яке наведене в базі знань. Для цього активуємо змінну y за допомогою натиснення лівої кнопки на блоці y. В правому верхньому куті можуть з’явитися позначення функцій належності, кожна з яких відповідає однієї лінійної залежності між входами і виходом. В базі знань, яка наведена на початку файлу, вказані 6 різних залежностей: y=-10; y=7; y=3,75 y=-3,75
Рис 3.2. Вікно лінійних залежностей «входи-вихід» Крок 13. Задамо найменування і параметри цих залежностей. Для цього робимо одне натиснення лівою кнопкою миші по імені першої залежності mf1. Потім друкуємо назву залежності, наприклад y=-10, в полі Name, і встановлюємо тип залежності – константа шляхом обирання опції Сonstant в меню Type. Після цього вводимо значення параметру – -10 в полі Params. Аналогічну процедуру робимо для другої змінної y=7. Для третьої функції mf3 введемо найменування, наприклад, y=3.75x1-10. Потім вкажемо лінійний тип залежності шляхом вибору опції Linear в меню Type і введемо параметри залежності 3.75 0 -10 в полі Params. Для лінійної залежності порядок параметрів наступний: перший параметр – коєфіцієнт при першій змінній, другий – при дрцгій і т.д., останній параметр – вільний член залежності. Таким ж чином введемо назви і параметри для всіх 6 функцій належності змінної y.
В результаті отримуємо графічне вікно, яке представлено на рис. 3.2.
Рис 3.3. Нечітка база знань для системи типу Сугено Крок 14. Перейдемо в редактор бази знань RuleEditor. Для цього оберемо в меню Edit команду Edit rules.... і введемо правила. Для вводу правила необхідно обрати відповідну комбінацію термів і залежностей і натиснути кнопку Add rule. На рис. 3.3 зображене вікно редактору бази знань після введення усіх 6 правил. На рис. 3.4 приведено вікно візуалізації нечіткого логічного виводу. Це вікно активується командою View rules... меню View. В полі Input вказуються значення вхідних змінних, для яких виконується логичний вивід. Як можна побачити з рисунку, значення вихідної змінної, розраховується як середнє зважене значення результатів виходу за кожним правилом.
Рис. 3.4 Візуалізація нечіткого логічного виводу для системи типу Сугено На рис. 3.5 приведена поверхня “входи-вихід”, яка відповідає синтезованій нечіткій системі. Для виведення цього вікна необхідно використати команду View surface... меню View. Порівнюючи цю поверхню і поверхню на рис. 1,можна зробити висновок, що нечіткі правила достатньо добре описують складну лінійну залежність. При цьому, модель типу Сугено більш точна. Перевага моделей типу Мамдані полягає у тому, що правила бази знань є прозорі і інтуїтивно зрозумілі, таді як для моделей типу Сугэно не завжди ясно які лінійні залежності «входи-вихід» необхідно використовувати.
Рис 3.5. Поверхня “вхід-вихід” для системи алгоритму Сугено
3.3 Завдання для самостійної роботи. 1. Створити систему нечіткого виводу Сугено, яка моделює залежність 2. Створити систему нечіткого виводу Сугено, яка відтворює поверхню 3. Створити систему нечіткого виводу Сугено, яка відтворює поверхню
Лабораторна робота №3 ПРОЕКТУВАННЯ СИСТЕМ КЕРУВАННЯ НА ОСНОВІ АЛГОРИТМІВ
Основні поняття Одним з основних напрямів використання СНВ є розв’язування задач керування. Під системою керування [5] будемо розуміти з’єднання
Рис. 4.1 Функціональний блок системи керування
в єдину конфігурацію, яка забезпечує їм необхідну поведінку для досягнення поставленої цілі. Зв'язок між входом (вектор-функцією
Рис. 4.2. Загальна схема системи керування
СК поділяють на розімкнені і замкнені. В розімкненій системі існує елемент – виконуючий пристрій, який визначає необхідне значення вхідного сигналу
Рис. 4.3. Загальна схема розімкнутої системи керування
В СК елемент, який «приймає рішення» будемо називати активним. Якщо система представляє собою конфігурацію активних елементів, її називають організаційною системою управління (ОСУ). Тоді в систему може входити елемент – координатор, який визначає вхідні сигнали активних елементів.
В замкненій системі існує зворотній зв’язок. Окремі елементи вхідного вектора
Рис. 4.4. Система керування зі зворотнім зв’язком
В якості прикладу розімкненої СУ може служити електронагрівальний пристрій, який керується кнопками завдання бажаної інтенсивності нагріву кімнати. Тоді вхідним сигналом є натиснення відповідної кнопки, а виходом – температура нагріву. Як замкнену систему управління можна розглянути керування автомобілем на дорозі. Тут в якості вхідних елементів виступають кут повороту руля та сила натискання педалей, в якості вихідних елементів виступають швидкість та напрямок руху автомобіля, а в якості вимірювання в зворотньому зв’язку виступають органи зору водія, які спостерігають напрямок траси і дозволені швидкості. Під керуванням (управлінням ) системою будемо розуміти таке визначення вхідного сигналу Побудова нечіткої моделі системи керування базується на формальному представленні характеристик об’єкту в термінах лінгвістичних змінних. В системі керування в якості лінгвістичних змінних розглядаються змінні входу і виходу системи. Ціль керування полягає у визначенні значень керуючих змінних (вхідних) змінних, реалізація яких забезпечує бажану поведінку чи бажаний стан об’єкту керування. Вихідні змінні можуть знову поступати на вхід системи, утворюючи зворотній зв'язок, як показано на рис.4.5.
Рис 4.5. Архітектура компонентів процесу нечіткого керування
Таким чином, нечітка модель системи керування може бути описана за допомогою апарату системи нечіткого виводу.
4.2 Методика розробки та використання системи
Розглянемо етапи побудови системи нечіткого виводу на основі прикладу побудови системи нечіткого керування процесом прийому на роботу у фірму нових співробітників. Нехай, у фірми є дві вакансії: програміст і системний адміністратор. Тому СНВ має дві вихідні лінгвістичні змінні
Менеджер по кадрам даної фірми розробив такі прості правила прийому на роботу: 1. Якщо досвід роботи високий і професійна освіта висока, то ймовірність прийняття на посаду програміста висока 2. Якщо досвід роботи високий і ділові якості гарні, то ймовірність прийняття на посаду системного адміністратора висока 3. Якщо досвід роботи і освіта високі, а ділові якості гарні, то ймовірність прийняття на роботу даної особи висока на обидві посади 4. Якщо досвід роботи невеликий, але освіта та ділові якості високі, тоді можливо прийняти на роботу таку особу в якості системного адміністратора 5. Якщо особа не має освіти і досвіду роботи, тоді прийняття її на роботу малоймовірне на обидві посади 6. Якщо професійна освіта висока, але досвід роботи і ділові якості невеликі тоді можна прийняти цю особу на посаду програміста і малоймовірно її прийняти на посаду системного адміністратора 7. Якщо освіти у особи немає, тоді малоймовірне її прийняття на роботу 8. Якщо особа не має досвіду роботи і її ділові якості не високі, тоді малоймовірне її прийняття на роботу на обидві посади 9. Якщо освіта особи висока, досвід роботи невеликий, то можливо прийняття її на роботу на посаду програміста 10. Якщо особа не має освіті і ділових якостей, то прийняття її на роботу малоймовірне на обидві посади 11. Якщо особа не має освіти, досвід і її ділові якості невисокі, тоді малоймовірне її прийняття на роботу на обидві посади 12. Якщо ділові якості особи невеликі, освіта професійна і досвід роботи високі, тоді малоймовірно її прийняти на посаду системного адміністратора і можливо її прийняти на посаду програміста.
Для розробки системи слід виконати наступні кроки.
Крок 1. Визначити вхідні і вихідні змінні. Очевидно, що для СНВ у якості вхідних змінних потрібно взяти 1) досвід роботи 2) освіту особи 3) ділові якості Далі слід задати терми цих змінних. Наприклад, для вхідної змінної досіду роботи можуть бути задані наступні терми: «немає», «невеликий», «високий» Крок 2. Фазифікація вхідних змінних. На цьому кроці слід задати функції належності для всіх термів вхідних змінних, а в якості області визначення – їх множини-носії Крок 3. Задати функції належності термів вихідних змінних (ймовірність прийняття на посаду) Крок 4. Ввести правила у базу правил. Крок 5. Використання моделі. Для цього розглянути приклад роботи системи керування при різних значеннях вхідної змінної. Для цього слід відкрити вікно правил
Рис. 4.6. Приклад термів змінної
Рис 4.7. Вікно дії правил
Рис 4.8 Поверхня СНВ задачі прийняття на роботу особи.
4.3 Завдання для самостійної роботи Завдання 1. Побудова системи керування діями офіцера дорожньої служби За допомогою СНВ алгоритму Мамдані побудувати базу знань, яка б консультувала офіцера дорожньої міліції що робити з машиною, яка наближається до контрольного пункту (пропустити, зупинити, перевірити документи, штрафувати або забирати права) в залежності від швидкості автомобіля та погодних умов, які можна задати за допомогою лінгвістичних змінних.
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 681; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.7.190 (0.012 с.) |

 на відрізку
на відрізку  (рис.2.1). Відмінність СНВ алгоритму Сугено полягає у проектуванні вихідних змінних. Формування бази правил систем нечіткого виводу наступного формату:
(рис.2.1). Відмінність СНВ алгоритму Сугено полягає у проектуванні вихідних змінних. Формування бази правил систем нечіткого виводу наступного формату: »
» »
»





 . Для лінгвістичної оцінки цієї змінної будемо використовувати 3 терми з трикутними функціями належності, які встановлені за замовченням. Задамо найменування термів змінної
. Для лінгвістичної оцінки цієї змінної будемо використовувати 3 терми з трикутними функціями належності, які встановлені за замовченням. Задамо найменування термів змінної 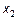 . Для лінгвістичної оцінки цієї змінної будемо використовувати 4 терми з трикутними функціями належності. Для цього активізуємо змінну
. Для лінгвістичної оцінки цієї змінної будемо використовувати 4 терми з трикутними функціями належності. Для цього активізуємо змінну  . Для цього надрукуємо 0 4 в полі Range і натиснемо <Enter>. Задамо найменування 4 термів (наприклад, L Низький, A Середній, HA Вище середнього, H Високий).
. Для цього надрукуємо 0 4 в полі Range і натиснемо <Enter>. Задамо найменування 4 термів (наприклад, L Низький, A Середній, HA Вище середнього, H Високий).





 при
при  .
. при
при 
 при
при  елементів
елементів  виду
виду

 ) і виходом (вектор-функцією
) і виходом (вектор-функцією  ) в елементі системи (функціональному блоці) – це перетворення одного сигналу (причини) в інший (наслідок). Вся система керування (СК) теж може бути представлення аналогічною схемою:
) в елементі системи (функціональному блоці) – це перетворення одного сигналу (причини) в інший (наслідок). Вся система керування (СК) теж може бути представлення аналогічною схемою:
 («приймає рішення» про необхідний вплив на систему) в залежності від бажаного (необхідного) значення виходу
(«приймає рішення» про необхідний вплив на систему) в залежності від бажаного (необхідного) значення виходу  :
:
 , які можна назвати керуючими змінними, залежать від різниці між бажаним значенням вихідних величин і їх реальним значенням
, які можна назвати керуючими змінними, залежать від різниці між бажаним значенням вихідних величин і їх реальним значенням  (негативний зворотній зв’язок) або від суми цих значень
(негативний зворотній зв’язок) або від суми цих значень  (позитивний зворотній зв’язок):
(позитивний зворотній зв’язок):
 ) системи для досягнення бажаних значень
) системи для досягнення бажаних значень  .
.
 з множинами-носіями у вигляді відрізків
з множинами-носіями у вигляді відрізків  , які інтерпретується як імовірність прийняття деякої особи на роботу відповідно на першу чи другу посаду. Вхідні змінні мають характеризувати особу, яка подала резюме про себе в фірми з метою влаштуватися на роботу. Наприклад,
, які інтерпретується як імовірність прийняття деякої особи на роботу відповідно на першу чи другу посаду. Вхідні змінні мають характеризувати особу, яка подала резюме про себе в фірми з метою влаштуватися на роботу. Наприклад,  - ділові якості спілкування.
- ділові якості спілкування. ;
; .
. і переглянути можливі значення вихідної змінної прийняття рішення про прийом на роботу в залежності від зміни значень вхідних змінних.
і переглянути можливі значення вихідної змінної прийняття рішення про прийом на роботу в залежності від зміни значень вхідних змінних.





