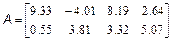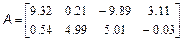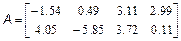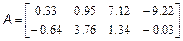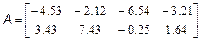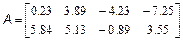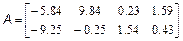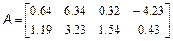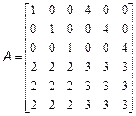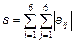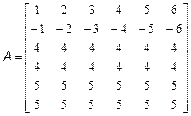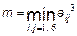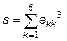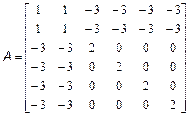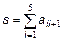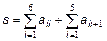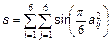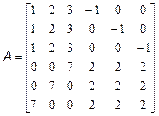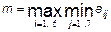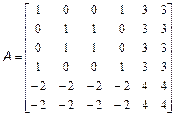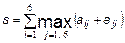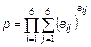Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вектор-рядки і вектор-стовпціСодержание книги
Поиск на нашем сайте До особливостей роботи з масивами в MatLab відноситься те, що одновимірний масив може бути вектор-рядком або вектор-стовпця. Якщо спосіб представлення масиву важливий, то ми підкреслюватимемо, про рядок або про стовпець йдеться. Якщо ж це несуттєво, то говоритимемо про вектор-рядки і вектор-стовпців просто як про вектори або одновимірні масиви (одновимірний масив в MatLab є двовимірний, у якого один з розмірів рівний одиниці). Для введення вектора використовуються квадратні дужки, елементи вектора відокремлюються один від одного: · крапкою з комою, якщо потрібно отримати вектор-стовбець; · пропуском або комою, якщо необхідно розмістити елементи у вектор-рядку. Наприклад, щоб занести вектор-стовпці і вектор-рядки
у відповідні масиви, слід набрати в командному рядку: >> a=[0.2; -3.9; 4.6]; >> b=[7.6; 0.1; 2.5]; >> u=[0.1 0.5 -3.7 8.1]; >> v=[5.2 9.7 3.4 –0.2]; Крапка з комою в кінці кожного рядка поставлена для придушення висновку на екран, вона ніяк не пов'язана з крапкою з комою, яка є роздільником елементів у вектор-стовпцях. Виведіть в командне вікно значення змінних а, b, u, v і побачите, як MatLab відображає вміст вектор-рядків і вектор-стовпців. Отримаєте інформацію про змінних за допомогою команди whos. Для отримання довжини вектора призначена функція length, вектор вказується як її вхідний аргумент: >> L=length(a) L = Вектор-стовпці з однаковим числом елементів можна складати і віднімати один з одного за допомогою знаків "+" і "–". Аналогічне вірно і для вектор-рядків: >> с=a+b; >> w=u-v; Складання і віднімання вектор-рядка і вектор-стовпця або векторів різних розмірів приводить до помилки. Операція * призначена для множення векторів за правилом матричного множення. Оскільки MatLab розрізняє вектор-рядки і вектор стовпці, то допустимо або множення вектор-рядка на такій же по довжині вектор-стовпець (скалярний добуток), або множення вектор-стовпця на вектор-рядок (зовнішній добуток, в результаті якого виходить прямокутна матриця). Скалярний добуток двох векторів повертає функція dot, а векторне — cross: >> s=dot(а,b) >> c=cross(а,b) Зрозуміло, векторний добуток визначений тільки для векторів з трьох елементів. Для операції транспонування зарезервований апостроф '. Якщо вектор містить комплексні числа, то операція ' призводить до комплексно-зв'язаного вектора. При обчисленні скалярного і векторного добутків функціями cross і dot не обов'язково стежити за тим, щоб обидва вектори були або стовпцями, або рядками. Результат виходить вірний, наприклад, при зверненні c=cross(а,b'), лише із стає вектор-рядком. MatLab підтримує по-елементні операції з векторами. Разом з множенням за правилом матричного множення, існує операція по-елементного множення.* (крапка із зірочкою). Дана операція застосовується до векторів однакової довжини і приводить до вектора тієї ж довжини, що вихідний, елементи якого рівні добутку відповідних елементів початкових векторів. Наприклад, для векторів а і b, введених вище, по-елементне множення дає слідуючий результат: >> c=a.*b c = 1.5200 -0.3900 11.5000 Аналогічним чином працює по-елементне ділення./ (крапка з косою межею). Крім того, операція.\ (крапка із зворотною косою межею) здійснює зворотне по-елементне ділення, тобто вирази а./b і b.\a еквівалентні. Зведення елементів вектора а в ступені, рівні відповідним елементам b, проводиться з використанням.^. Для транспонування вектор-рядків або вектор-стовпців призначено поєднання.' (крапка з апострофом). Операції ' і.' для речовинних векторів приводять до однакових результатів. Не обов'язково застосовувати по-елементні операції при множенні вектора на число і числа на вектор, діленні вектора на число, складанні і відніманні вектора і числа. При виконанні, наприклад, операції a*2, результат є вектор того ж розміру, що і а, з подвоєними елементами. Вектори можуть бути аргументами вбудованих математичних функцій, таких, як sin, cos і т.д. В результаті виходить вектор з елементами, рівними значенню функції, що викликається, від відповідних елементів початкового вектора, наприклад: >> q=sin([0 pi/2 pi]) q = 0 1.0000 0.0000 Однак для обчислення складнішої функції від вектора значень, скажімо
слід записати >> f=(v.*sin(v)+v.^2)./(v+1) Часто потрібно обчислити функцію від вектора значень аргументу, що відрізняються один від одного на постійний крок. Для створення таких вектор-рядків передбачена двокрапка. Послідовність команд >> x=-1.2:0.5:1.8; >> f=(x.*sin(x)+x.^2)./(x+1); Призводить до заповнення наступних векторів: >> x x = -1.2000 -0.7000 -0.2000 0.3000 0.8000 1.3000 1.8000 >> f f = -12.7922 3.1365 0.0997 0.1374 0.6744 1.2794 1.7832 Крок може бути негативним, в цьому випадку початкове значення повинне бути більше, або рівно кінцевому для отримання не порожнього вектора. Якщо крок рівний одиниці, то його можна не вказувати, наприклад: >> n=-3:4 n = -3 -2 -1 0 1 2 3 4 Ясно, що для заповнення вектор-стовпця елементами з постійним кроком слід транспонувати вектор-рядок. Створення векторів за допомогою двокрапки і уміння проводити по-елементні операції необхідне для візуалізації масивів даних, про що буде сказано в наступних розділах. MatLab володіє великим набором вбудованих функцій для обробки векторних даних, частина з них приведена в табл. 2.1. Повний список наявних функцій виводиться в командне вікно за допомогою help datafun. Звернете увагу на те, що ряд функцій допускає звернення до них як з одним, так і з двома вихідними аргументами. У разі декількох вихідних аргументів вони полягають в квадратні дужки і відділяються один від одного коми. Дуже часто потрібно обробити тільки частину вектора, або звернутися до деяких його елементам. Розберемо правила MatLab, по яких проводиться індексація векторних даних. Для доступу до елементу вектора необхідно вказати його номер в круглих дужках відразу після імені змінної, в якій міститься вектор. Наприклад, сума першого і третього елементів вектора v знаходиться за допомогою виразу >> s=v(1)+v(3); Звернення до останнього елементу вектора можна провести з використанням end, тобто v(end) і v(length(v)) приводять до однакових результатів.
Таблиця. Д2.1 Функції обробки даних
Вказівку номерів елементів вектора можна використовувати і при введенні векторів, послідовно додаючи нові елементи (не обов'язково в порядку зростання їх номерів). Команди: >> h=10; >> h(2)=20; >> h(4)=40; приводять до утворення вектора: >> h h = 10 20 0 40 Зауважте, що для введення першого елементу h не обов'язково вказувати його індекс, оскільки при виконанні оператора h=1 створюється вектор (масив розміру один на один). Наступні оператори привласнення приводять до автоматичного збільшення довжини вектора h, а пропущені елементи (у нашому випадку h(3)) набувають значення нуль. Індексація двокрапкою дозволяє виділити що йдуть підряд елементи в новий вектор. Початковий і кінцевий номери вказуються в круглих дужках через двокрапку, наприклад: >> z=[0.2 -3.8 7.9 4.5 7.2 -8.1 3.4]; >> znew=z(3:6) znew = 7.9000 4.5000 7.2000 -8.1000 Індексація вектором служить для виділення елементів із заданими індексами в новий вектор. Індексний вектор повинен містити номери необхідних елементів, наприклад: >> ind=[3 5 7]; >> znew=z(ind) znew = 7.9000 7.2000 3.4000 Конструювання нових векторів з елементів наявних векторів проводиться за допомогою квадратних дужок. Наступний оператор призводить до утворення вектора, в якому пропущений п'ятий елемент вектора z >> znew=[z(1:4) z(6:end)] znew = 0.2000 -3.8000 7.9000 4.5000 -8.1000 3.4000 Завдання для самостійної роботи Для заданих векторів а і b довжини n: 1. обчислити їх суму, різницю і скалярний добуток; 2. утворити вектор 3. упорядкувати вектор за збільшенням і убуванню; 4. переставити елементи вектора в зворотному порядку і записати результат в новий вектор; 5. знайти векторний добуток Варіанти
Обчислити значення функції на відрізку в заданому числі N, рівномірно віддалених один від одного точок. Варіанти
Матриці Матриці невеликих розмірів зручно вводити з командного рядка. Існує три способи введення матриць. Наприклад, матрицю
можна ввести таким чином: набрати в командному рядку (розділяючи елементи рядка матриці пропусками): A=[0.7 2.5 9.1 і натиснути <Enter>. Курсор переміщається в наступний рядок (символ запрошення командного рядка >> відсутній). Елементи кожного наступного рядка матриці набираються через пропуск, а введення рядка завершується натисненням на <Enter>. При введенні останнього рядка в кінці ставиться закриваюча квадратна дужка: >> A=[0.7 -2.5 9.1 8.4 0.3 1.7 -3.5 6.2 4.7] Якщо після закриваючої квадратної дужки не ставити крапку з комою для придушення висновку в командне вікно, то матриця виведеться у вигляді таблиці. Інший спосіб введення матриці заснований на тому, що матрицю можна розглядати як вектор-стовпець, кожен елемент якого є рядком матриці. Оскільки крапка з комою використовується для розділення елементів вектор-стовпця, то введення, наприклад, матриці
здійснюється оператором привласнення: >> B=[6.1 0.3; -7.9 4.4; 2.5 -8.1]; Введіть матрицю B і відобразіть її вміст в командному вікні, набравши в командному рядку B і натиснувши <Enter>. Очевидно, що допустиме таке трактування матриці, при якій вона вважається вектор-рядком, кожен елемент якого є стовпцем матриці. Отже, для введення матриці
досить скористатися командою: >> C=[[0.4; 0.1] [-7.2; -2.1] [5.3; -9.5]] Звернете увагу, що внутрішні квадратні дужки дійсно потрібні. Оператор C=[0.4; 0.1 -7.2; -2.1 5.3; -9.5] є неприпустимим і приводить до повідомлення про помилку, оскільки виявляється, що в першому рядку матриці міститься тільки один елемент, в другій і третій по два, а в четвертій — знову один. Скористайтеся командою whos для отримання інформації про змінних A, B і C робочого середовища. У командне вікно виводиться таблиця з інформацією про розміри масивів, пам'ять, необхідну для зберігання кожного з масивів, і тип — double array. Функція size дозволяє встановити розміри масивів, вона повертає результат у вигляді вектора, перший елемент якого рівний числу рядків, а другою стовпців: >> s=size(B) s = 3 2 Складання і віднімання матриць однакових розмірів проводиться з використанням знаків +, -. Зірочка * служить для обчислення матричного добутку, причому відповідні розміри матриць повинні збігатися, наприклад: >> P=A*B P = 46.7700 -84.5000 53.1200 -9.9300 -58.5800 -11.8400 Допустиме множення матриці на число і числа на матрицю, при цьому відбувається множення кожного елементу матриці на число і результатом є матриця тих же розмірів, що і вихідна. Апостроф ' призначений для транспонування речовинної матриці або знаходження зв'язаною до комплексної матриці. Для піднесення квадратної матриці до ступеня застосовується знак ^. Наприклад, обчислення матричного виразу >> R=(A-B*C)^3+A*B*C R = 1.0e+006 * -0.0454 0.1661 -0.6579 0.0812 -0.2770 1.2906 -0.0426 0.1274 -0.7871 MatLab володіє різноманіттям різних функцій і способів для роботи з матричними даними. Для звернення до елементу двовимірного масиву слід вказати його рядковий і стовпцеві індекси в круглих дужках після імені масиву, наприклад: >> C(1,2) ans = -7.2000 Індексація двокрапкою дозволяє отримати частину матриці — рядок, стовпець або блок, наприклад: >> c1=A(2:3,2) c1 = 0.3000 6.2000 >> r1=A(1,1:3) r1 = 0.7000 -2.5000 9.1000 Для звернення до всього рядка або всього стовпця не обов'язково указувати через двокрапку початковий (перший) і кінцевий індекси, тобто оператори r1=A(1,1:3) і r1=A(1:) еквівалентні. Для доступу до елементів рядка або стовпця від заданого до останнього можна використовувати end, так само як і для векторів: A(1,2:end). Виділення блоку, що складається з декількох рядків і стовпців, вимагає індексації двокрапкою як по першому вимірюванню, так і по другому. Нехай в масиві T зберігається матриця:
Для виділення її елементів з другого рядка по третю і з другого стовпця по четвертий досить використовувати оператор: >> T1=T(2:3,2:4) T1 = -5 -6 3 4 5 -1 Індексація двокрапкою так само дуже корисна при різних перестановках в масивах. Зокрема, для перестановки першого і останнього рядків в довільній матриці, що зберігається в масиві A, підійде послідовність команд: >> s=A(1:); >> A(1:)=A(end:); >> A(end:)=s; MatLab підтримує таку операцію, як викреслювання рядків або стовпців з матриці. Блоку, що достатньо віддаляється, привласнити порожній масив, що задається квадратними дужками. Наприклад, викреслювання другого і третього рядка з масиву T, запровадженого вище, проводиться наступною командою: >> T(2:3:)=[] T = 1 7 -3 2 4 9 -6 -4 7 2 6 1 Індексація двокрапкою спрощує заповнення матриць, що мають певну структуру. Припустимо, що потрібно створити матрицю
Перший крок полягає у визначенні нульової матриці розміру п'ять на п'ять, потім заповнюються перший і останній рядки і перший і останній стовпці: >> W(1:5,1:5)=0; >> W(1:)=1; >> W(end:)=1; >> W(:,1)=1; >> W(:,end)=1; Перевірте, що в результаті виходить необхідна матриця. Низка вбудованих функцій, приведених в табл.3.1, дозволяє ввести стандартні матриці заданих розмірів. Звернете увагу, що у всіх функціях, крім diag, допустимо вказувати розміри матриці наступними способами:
Останній варіант дуже зручний, коли потрібно створити стандартну матрицю тих же розмірів, що і деяка наявна матриця. Якщо, наприклад, A була визначена раніше, то команда I=eye(size(A)) призводить до появи по-одиночній матриці, розміри якої збігатися з розмірами A, оскільки функція size повертає розміри матриці у векторі. Розберемо, як отримати трьох-діагональну матрицю розміру сім на сім, приведену нижче, з використанням функцій MatLab.
Введемо вектор v з цілими числами від одного до семи і використаємо його для створення діагональної матриці і матриці із зміщеною на одиницю вгору діагоналлю. Вектор довжини шість, що містить п'ятірки, заповнюється, наприклад, так: 5*ones(1,6). Цей вектор вкажіть в першому аргументі функції diag, а мінус одиницю — в другому і отримаєте третю допоміжну матрицю. Тепер досить відняти з першої матриці другу і скласти з третьою: >> T=diag(v) -diag(v(1:6),1)+diag(5*ones(1,6)-1) Таблиця. 3.1 Функції для створення стандартних матриць
По-елементні обчислення з матрицями проводяться практично аналогічно як і для векторів з необхідністю, зрозуміло, стеження за збігом розмірів матриць: A.*B, A./B— по-елементне множення і ділення; A.^p — по-елементне піднесення до ступеня, p — число; A.^B — піднесення елементів матриці A до ступенів, рівних відповідним елементам матриці B; A.' — транспонування матриці (для речовинних матриць A' і A.' приводять до однакових результатів); Іноді потрібно не просто транспонувати матрицю, але і "розвернути" її. Розворот матриці на 90o проти годинникової стрілки здійснює функція rot90: >> Q=[1 2;3 4] Q = 1 2 3 4 >> R=rot90(Q) R = 2 4 1 3 Допустимо записувати суму і різницю матриці і числа, при цьому складання або віднімання застосовується, відповідно, до всіх елементів матриці. Виклик математичної функції від матриці призводить до матриці того ж розміру, на відповідних позиціях якої коштують значення функції від елементів початкової матриці. У MatLab визначені і матричні функції, наприклад, sqrtm призначена для обчислення квадратного кореня. Знайдіть квадратний корінь з матриці
і перевірте отриманий результат, звівши його в квадрат (за правилом матричного множення, а не по-елементно): >> K=[3 2; 1 4]; >> S=sqrtm(K) S = 1.6882 0.5479 0.2740 1.9621 >> S*S ans = 3.0000 2.0000 1.0000 4.0000 Матрична експонента обчислюється з використанням expm. Спеціальна функція funm служить для обчислення довільної матричної функції. Всі функції обробки даних, приведені в табл. 2.1, можуть бути застосовані і до двовимірних масивів. Основна відмінність від обробки векторних даних полягає в тому, що ці функції працюють з двовимірними масивами по стовпцях, наприклад, функція sum підсумовує елементи кожного із стовпців і повертає вектор-рядок, довжина якого рівна числу стовпців початкової матриці: >> M=[1 2 3; 4 5 6; 7 8 9] M = 1 2 3 4 5 6 7 8 9 >> s=sum(M) s = 12 15 18 Якщо як другий вхідний аргумент sum вказати 2, то підсумовування відбудеться по рядках. Для обчислення суми всіх елементів матриці потрібно двічі застосувати sum: >> s=sum(sum(M)) s = Дуже зручною можливістю MatLab є конструювання матриці з матриць менших розмірів. Нехай задані матриці:
Потрібно скласти блокову матрицю M: Можна вважати, що має розміри два на два, а кожен елемент є, відповідно, матрицею, або M4. Отже, для отримання в робочому середовищі MatLab масиву M з матрицею потрібно використовувати оператора: >> M=[M1 M2; M3 M4] Завдання для самостійної роботи 1. Введіть матриці
і знайдіть значення наступних виразів. Варіанти 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 2. За допомогою вбудованих функцій для заповнення стандартних матриць, індексації двокрапкою і, можливо, повороту, транспонування або викреслювання отримаєте наступні матриці: Варіанти
1. 2. 3. 4. 5. 6. 7. 8. 9. 10.
3. Обчислити значення функції для всіх елементів матриці і записати результат в матрицю того ж розміру, що і вихідна. Варіанти
4. Сконструювати блокові матриці (використовуючи функції для заповнення стандартних матриць) і застосувати функції обробки даних і по-елементні операції для знаходження заданих величин. Варіанти 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. .
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 2179; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.009 с.) |

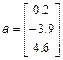
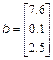
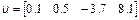

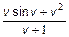
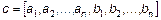 , визначити його максимальний і мінімальний елементи і поміняти їх місцями;
, визначити його максимальний і мінімальний елементи і поміняти їх місцями;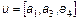 і
і  .
.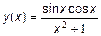
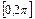
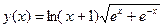
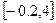
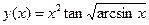
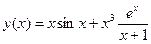
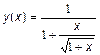
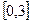
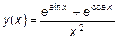
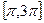

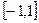
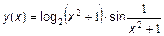

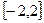
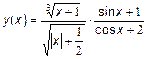
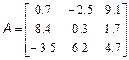
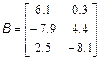

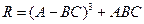 здійснується командою:
здійснується командою: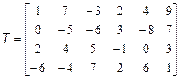
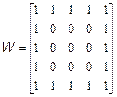
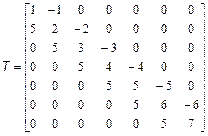
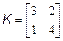

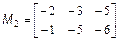
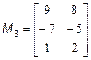
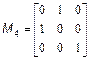
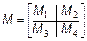
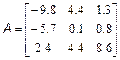
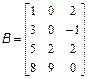
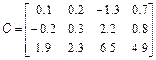

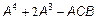
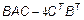
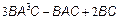
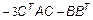
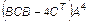
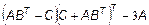
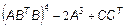
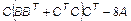
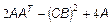

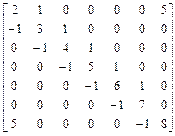

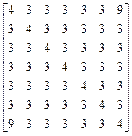
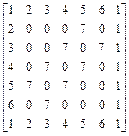


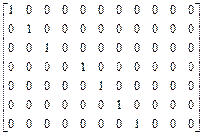
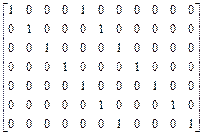
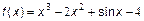 ;
2.
;
2. 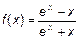 ;
3.
;
3. 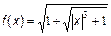 ;
4.
;
4. 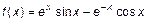 ;
5.
;
5. 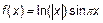 ;
6.
;
6. 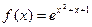 ;
7.
;
7.  ;
8.
;
8. 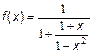 ;
9.
;
9.  ;
10.
;
10.  ;
;