Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Способи усунення та/або врахування нечіткості знаньСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Практична робота №17 Механізм висновку Мета роботи: Здобуття практичних навичок отримання висновків на нечітких даних про об’єкти і процеси інформаційної безпеки Теоретичні відомості Процедура обробки нечітких правил складається з 4 етапів. Етап 1. Обчислення значень функцій приналежності (істинності) для нечітких множин ЛП, що входить в ліві частини правил. Етап 2. Модифікація нечітких множин для ЛП, зазначеної в правій частині правил, відповідно до значень функції приналежності, отриманими на першому етапі. Етап 3. Об'єднання (суперпозиція) модифікованих множин. Етап 4. скаляризації результату суперпозиції - перехід від НМ до скалярним значенням. Приклад використання нечітких множин Розглянемо приклад того, як обробляються нечіткі правила виведення в системі, що управляє вентилятором кімнатного кондиціонера. Завдання кондиціонера - підтримувати оптимальну температуру повітря в кімнаті (t), охолоджуючи його, коли жарко, і нагріваючи, коли холодно. Нехай, змінюючи швидкість обертання вентилятора (V), що проганяє повітря через охолоджувальний елемент, ми можемо змінювати температуру повітря, тоді алгоритм роботи кондиціонера може бути заданий такими правилами: 1. ЯКЩО t = "висока", ТО V = "висока". 2. ЯКЩО t = "середня", ТО V = "середня". 3. ЯКЩО t = "низька", ТО V = "низька". Для того щоб система могла обробляти ці правила, треба задати функції належності для нечітких підмножин, визначених на значеннях температури і швидкості обертання вентилятора. Нехай температура повітря в кімнаті знаходиться в межах від 0 ° С до 60 ° С, а швидкість обертання вентилятора від 0 до 1000 об / хв. НМ для температури і швидкості обертання показані на ріс.3.6-3.11.
Рис.3.6. НМ «низька t»
Рис.3.7. НМ «середня t»
Рис.3.8. НМ «висока t»
Рис.3.9. НМ «низька V»
Рис.3.10. НМ «середня V»
Рис.3.11. НМ «висока V» Тепер розглянемо, як нечітка керуюча система визначає швидкість обертання вентилятора залежно від температури повітря в кімнаті. Припустимо, що початкова температура дорівнює 22 ° C. Етап 1. У лівих частинах правил вказані три НМ, заданих на інтервалі t. Знаходимо значення функції приналежності: m Tнізкая (22) = 0, m Tсредняя (22) = 0.8 і m Tвисокая (22) = 0.2. Етап 2. Отримані значення використовуємо для модифікації нечітких множин правих частин методом «множення».
Рис.3.12. Модифікація НМ Етап 3. Об'єднання (суперпозиція) результатів модифікації НМ.
Рис.3.13. Об'єднання результатів модифікації Етап 4. Для отримання скалярного значення, розраховують центр ваги отриманої фігури. Для зазначеної на рис.3.13 фігури центр знаходитися в точці V = 560.57 об / хв. Виникає питання, чи виправдана настільки складна система управління таким простим пристроєм? Практика показує, що виправдана. Так, наприклад, кондиціонери, засновані на нечіткій логіці, забезпечують менші в порівнянні з традиційними коливання температури, швидше пристосовуються до зовнішніх умов і дають істотну економію електроенергії. На рис.3.14 показані графіки зміни температури повітря в приміщенні при порівнянні системи, заснованої на нечіткій логіці, і традиційної системи.
Рис.3.14. Графіки зміни температури повітря - імовірнісний підхід на основі теореми Байєса; Нечіткі множини в системах керування Вдалим застосуванням теорії нечітких множин є контролери нечіткої логіки. Їх функціонування дещо відрізняється від роботи звичайних контролерів; для опису системи замість диференційних рівнянь використовуються знання експертів. Ці знання можуть бути виражені за допомогою лінгвістичних змінних, які описані нечіткими множинами. Таблиця нечітких правил
Кожний запис в даній таблиці відповідає своєму нечіткому правилу, наприклад: Якщо дистанція близько і напрямок правий, тоді рульовий кут різко вліво Таким чином, мобільний робот з нечіткою логікою буде працювати за наступним принципом: дані з сенсорів про відстань до перешкоди та напрямок до неї будуть фазіфіковані, оброблені згідно табличних правил, дефазіфіковані і отримані дані у вигляді керуючих сигналів надходять на приводи робота. Переваги нечітких систем · Можливість оперувати вхідними даними, заданими нечітко: наприклад, дані, які неперервно змінюються в часі (динамічні задачі), значення, що неможливо задати однозначно (результати статистичних опитувань, рекламні компанії); · Можливість нечіткої формалізації критеріїв оцінки і порівняння: оперування критеріями "більшість", "можливе", переважно" тощо.; · Можливість проведення якісних оцінок як вхідних даних, так і виведених результатів: значення даних, їх ступень достовірності (не плутати з імовірністю!) та її розподілом; · Можливість проведення швидкого моделювання складних динамічних систем та їх порівняльний аналіз із заданим ступенем точності: оперуючи принципами поведінки системи, описаними fuzzy-методами: o можна швидко з'ясувати точні значення змінних і скласти правила, що їх описують, o можна оцінити різні варіанти вихідних значень. Проектування модуля нечіткого управління
Визначення універсумів
Модуль нечіткого управління повинен моделювати невідому нам математичну залежність Y=F(X), Y={y1, y2,…, yi,…, ym} - вектор оптимальних виходів (вектор функцій мети); X={ x1, x2,…, xj,…, xn } – вектор вхідних змінних; i=1,2,…,m – порядковий номер елементів вектору Y; j=1, 2, …, n - порядковий номер елементів вектору Х.
Нечітка база знань може мати різні виходи: у вигляді термів (модель Мамдані) та у вигляді лінійної математичної функції залежності від змінних входу (модель Такагі-Сугено). Розглянемо спочатку модель Мамдані. ELSE
OR …
ELSE
OR …
OR …
ELSE (11.8)
OR …
Подібну систему логічних висловлень, яку називають нечіткою базою знань, можна компактно записати як
Тут записане одне р -те об’єднане логічне висловлювання із (11.8) з використанням операцій Таким чином, невідома залежність Y=F(X) формально замінюється нечіткими логічними висловлюваннями (11.9), які базуються на створеній експертом матриці знань табл. 11.5. Формування системи нечітких логічних рівнянь для моделі Мамдані Для отримання висновку за Мамдані при формуванні системи нечітких логічних рівнянь система логічних висловлювань (11.9) перетворюється наступним чинам: 1. Вхідні лінгвістичні оцінки (терми) 2. Вагові коефіцієнти 3. Логічне AND замінюється знаком 4. Вихідна лінгвістична оцінка (терм bр) змінної виходу у замінюється відповідною функцією належності В результаті отримуємо систему логічних рівнянь:
………………………………………………………
………………………………………………………
………………………………………………………
………………………………………………………
…………………………………………………………………………….
………………………………………………………
………………………………………………………
…………………………………………………………………………….
………………………………………………………
………………………………………………………
За аналогією з (11.9) систему логічних рівнянь (11.10) можна компактно записати як
Тут записане одне р -те об’єднане логічне рівняння із (11.10) з використанням операцій Таким чином, невідома нам залежність Y=F(X) формально замінюється нечіткими логічними рівняннями (11.11), які базуються на створеній експертом матриці знань табл.11.5. Робота блоку дефаззифікації при отриманні висновку за моделлю Мамдані Основне призначення блоку дефаззифікації – видати на виході нечіткої системи управління числовий сигнал виходу 1. Блок нечіткого логічного висновку для кожного k– ого правила бази нечітких знань визначає вигляд вихідної функції належності а) метод дефаззифікації по середньому центру (англ.. center average defuzzification), за яким числове значення у* розраховується за формулою
де yk* - точка у вигляді числового значення, в якій функція належності μk(у) отримує максимальне числове значення на універсумі виходу Uy;
Перевагою методу є те, що отримане рішення у вигляді числа не залежить від форми функції μk (у) та нечіткої множини
б) метод дефаззифікації по сумі центрів (англ.. center of sums defuzzification), за яким числове значення у* розраховується по величинам інтегралів
Цей метод може використовуватися, якщо ФН 2. Блок нечіткого логічного висновку об’єднує висновки усіх правил: вихідні дані
б) за методом центру тяжіння (центру ваги, центру площини) (англ.. center of gravity method, center of area method), згідно з яким вихід нечіткої системи управління
Цей метод є найбільш розповсюдженим. Тут інтегрування по у може розглядатись у як у межах всього універсуму Uy, так і в межах носія НМ Океания И.Г., Филиппов А.В. Кременчугский университет экономики, информационных технологий и управления. Задача прийняття рішень - одна з найпоширеніших в будь-якій предметній області. Її рішення зводиться до вибору однієї або декількох кращих альтернатив з деякого набору. Для того, щоб зробити такий вибір, необхідно чітко визначити мету та критерії (показники якості), за якими буде проводитися оцінка деякого набору альтернативних варіантів. Вибір методу вирішення такого завдання залежить від кількості і якості доступної інформації. Дані, необхідні для здійснення обґрунтованого вибору, можна розділити на чотири категорії: інформація про альтернативні варіанти, інформація про критерії вибору, інформація про уподобання, інформація про оточення завдання. З множини відомих методів і підходів до прийняття рішень найбільший інтерес представляють ті, які дають можливість враховувати багатокритеріальність і невизначеність, а також дозволяють здійснювати вибір рішень з множин альтернатив різного типу при наявності критеріїв, що мають різні типи шкал вимірювання. Одним з таких методів є метод багатокритеріального вибору альтернатив на основі композиційного правила агрегування альтернатив з інформацією про уподобання особи, що приймає рішення, які задані у вигляді нечітких суджень. Як приклад розглянемо задачу вибору співробітника служби безпеки з Придатність претендента на посаду оцінюється за системою правил Наприклад,
В словесній формі ці правила мають наступний вигляд:
Спочатку кожний претендент
Припустимо, що для п’яти претендентів
Нехай U - множина елементів, А - її нечітка підмножина, ступінь належності елементів до якої є числом з одиничного інтервалу [0, 1]. Елементи підмножини А є значеннями лінгвістичної змінної X. Припустимо, що множина рішень характеризується набором критеріїв xj, х 2,..., xn, тобто лінгвістичних змінних, заданих на базових множинах Uj, U 2,..., Un. Набір з декількох критеріїв з відповідними значеннями ФН характеризує уявлення особи, що приймає рішення, про якість альтернативи. Для осмислення задовільності кожної з альтернатив застосуємо правило композиційного виведення Е, = G, ° D, де Е, - ступінь задоволення альтернативи до, G, - відображення альтернативи до у вигляді нечіткого підмножини на U, D - загальне функціональне рішення. Тоді /(а(.*) = тах (ГШП (/ (а (і), кол (і))). Зіставлення альтернатив відбувається на основі точкових оцінок. Для нечіткої множини С з 1 визначаємо а- уровневое множина (<Х? [0, 1]) С "= {и | / ІЕ (і) га, іє7}. Кращою вважається альтернатива з найбільшим значенням точкової оцінки. Операції перетину нечітких множин відповідає знаходження мінімуму їх функцій належності де V = UlxU2x... xUp, v = (ul, u1,..., up), iiA (Uj) -значення функції приналежності елемента ut нечіткій множині Аг Для додання спільності судженням позначимо базові множини І / і Гчерез Ж Тоді А - нечітке підмножина W, в той час як В-нечітке підмножина одиничного інтервалу І. Для представлення правил використовується операція імплікації, для якої запропоновані різні способи нечіткої реалізації, наприклад, нечітка імплікація Лукасевича у вигляді / (ц (№, /) = тіп (і, (й-, ід (і>))) Висловлювання di, d1,..., ^ перетворюються в нечіткі множини Н,, Ні,..., НЧ- Їх перетином є множина П.... пН (і для кожного (w, i) eWxf Розглянутий метод прийняття рішень з використанням правил нечіткого виводу є адаптацією нечіткої логіки до процесів прийняття рішень з вихідними даними у вигляді точкових оцінок. Из множества известных методов и подходов к принятию решений наибольший интерес представляют те, которые дают возможность учитывать многокритериальность и неопределенность, а также позволяют осуществлять выбор решений из множеств альтернатив различного типа при наличии критериев, имеющих разные типы шкал измерения. В рамках данной работы рассматривается метод многокритериального выбора альтернатив на основе композиционного правила агрегирования альтернатив с информацией о предпочтениях лица, принимающего решение, которые заданы в виде нечетких суждений.
Пусть U — множество элементов, А - его нечеткое подмножество, степень принадлежности элементов к которому есть число из единичного интервала [0, 1]. Элементы подмножества А являются значениями лингвистической переменной X, Допустим, что множество решений характеризуется набором критериев xj, х2,...,*„ т.е. лингвистических переменных, заданных на базовых множествах и;, ц^,.., щ соответственно. Набор из нескольких критериев с соответствующими значениями характеризует представление лица, принимающего решение, об удовлетворительности альтернативы. Операции пересечения нечетких множеств соответствует нахождение минимума их функций принадлежности
где V = UlxU2x...xUp,v = (ul,u1,...,up),iiA (Uj) -значение функции принадлежности элемента ut нечеткому множеству Аг Для придания общности суждениям обозначим базовые множества І/ и Гчерез Ж Тогда А - нечеткое подмножество W, в то время как В-
нечеткое подмножество единичного интервала І. Для представления правил используется операция импликации, для которой предложены различные способы нечеткой реализации, например, нечеткая импликация Лукасевича в виде /(ц(№,/)=тіп(і,(і-,ид(и>)))
Высказывания di,d1,..., ^преобразуются в нечеткие множества
Н,,Ні,...,НЧ- Их пересечением является множество П....пН(и для каждого (w,i)eWxf
Для осмысления удовлетворительности каждой из альтернатив применим правило композиционного вывода Е, = G, ° D, где Е, - степень удовлетворения альтернативы к, G, - отображение альтернативы к в виде нечеткого подмножества на U, D - общее функциональное решение. Тогда /(а(.*) = тах(гшп(/(а(и), цв(и))). Сопоставление альтернатив
происходит на основе точечных оценок. Для нечеткого множества С с 1 определяем а- уровневое множество (<Х? [0, 1]) С„ ={і|/іе(і)га,іє7}. Лучшей считается альтернатива с наибольшим значением точечной оценки. Рассмотренный метод принятия решений с использованием правил нечеткого вывода является адаптацией нечеткой логики к процессам принятия решений с исходными данными в виде точечных оценок.
Зінченко Є. Г. Кременчуцький університет економіки, інформаційних технологій і управління. Однією з невід'ємних складових маркетингової діяльності є широке використання різних математичних методів і моделей [І]. Вони активно застосовуються при обробні зібраної маркетингової Інформації; без їх допомоги неможливо вирішувати завдання планування, аналізу та прогнозування діяльності підприємств [2]. Як показус практика, найбільш зручним і коректним методом вирішення проблем при плануванні рекламної діяльності стає методологія, що реалізується апаратом нечіткої математики. Для вирішення задачі вибору найбільш ефективного друкованого видання при плануванні рекламної кампанії пропонується застосовувати методику, яка використовується у системах типу «якщо - то», з певними модифікаціями. Множину можливих рекламних носіїв розглянемо як аналог набору еталонних ситуацій, які для кожного видання описують необхідні для аналізу параметри. Такими показниками можуть бути «розмір підприємства», «тираж видання» і «вартість розміщення рекламного блоку». При необхідності вибору одного або декількох рекламних носіїв рекламодавець визначає необхідні йому значення критеріїв відбору, які будуть описувати нечітку «робочу» ситуацію. Далі робимо її порівняння з кожним елементом з бази друкованих видань, після чого вони ранжуються в порядку їх ступеня близькості до «робочої» ситуації [3]. Наприклад, підприємство планує провести рекламну кампанію в друкованих засобах масової інформації (видання А, видання В, видання С). Видання будемо описувати в базі знань за допомогою ступенів відповідності «Понністю відповідає» (ступінь відповідності дорівнює 1), «Відповідає» (0,7), «Погано відповідає» (0,2) і «Не відповідає» (0). У формі опису нечітких ситуацій ці видання можуть бути описані наступним чином: Sa = {«1/Мале>,<0,7/Середнє>,<0/Велике>/Розмір підприємства^ «0,7/Не вели кий>,<1 /Сере дній>,<О/Великий>/Тираж видання>, <<0Д/Низька>,<0,7/Середня>,<0/Висока>/Вартістьрозміщення>}; Sb = {<<0,7/Мале>,<0.2/Середнє>,<0,7/Велике>/Розмір підприємства^ «О/Не великий>,<0,7/Середній>,<1/Великий>/Тираж видання>, «0,2/Низька>,<0,7/Серсдня>,<0,7/Висока>/Вартість розміщенні}; Sc = {«0/Мале>,<0,2/Середнє>,<0,7/Велнке>/Розмір підприємстві, «0,7/Не великий>,<0,7/Середній>,<0/ВеликиЙ>/Тираж видання>, «0/Низька>,<0,2/Середня>,<0,7/Висока>/ВаргістьрозмІщення>(. Ми плануємо провести рекламну кампанію в друкованих засобах масової інформації, причому нашою цільовою аудиторією є середні за розміром підприємства. Виходячи з наявного бюджету, нас цікавлять видання середнього тиражу, з середніми розцінками на розміщення рекламних блоків. Нечітка ситуація, що формалізує опис «еталонного видання» («робоча ситуація»), описується наступним чином:
Sc = {«0,7/Мале>,<1/Середнє>,<0/Велике>/Розмір підприємства^ «0,7/Не іеликий>,<1/Середній>,<0,2/ВеликиЙ>/Тираж видання>, <<0,7/Низька>,<0,7/Середня>,<0/Висока>/Вартістьрозміщення>}.
Визначимо ступені близькості видання, що описується нечіткою ситуацією So, до кожного з видань, які присутні в нашій базі даних. Ступінь близькості будемо оцінювати за допомогою відстані ХеммІнга [3] між Поточною ситуацією Sa до S,, je {А, В, CJ, що визначається за формулою: , ш де г, - і-й компонент вектора г : що описує видання *. Наприклад,
для гот = (0,7, 1, 0, 0,7, 1, 0,2, 0,7, 0,7, 0), Т - символ транспонування. Найбільш прийнятний варіант видання визначається за правилом: МЕТІТ-4 О Третя секція j j Маємо: D(Sa, SA) = 0,8; D{Sa, SB) = 4,5; ДЗр, Sc) = 4,6. Таким чином видання А с найбільш «близьким» до «еталонного видання», тому при проведенні рекламної кампанії найбільш економічно доцільним є розміщення реклами у виданні А. Запропонована методика дозволяє за заданими критеріями швидко відбирати видання з об'смної бази даних. Крім того, видання можуть бути різним чином класифіковані, до них можуть бути прив'язані інші чіткі і нечіткі, кількісні і якісні ознаки, за якими може проводитися попередній відбір, або вони можуть бути включені в процедуру ранжиру -вапня. Управління зарядом батареї. Акумуляторна батарея використовує джерело заряду від сонячних батарей і розряджається на навантаження. Напруга джерела заряду дозволяє заряджати батарею, у той час як навантаження р
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-24; просмотров: 416; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.225.188 (0.022 с.) |


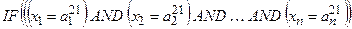 (з вагою w 21)
(з вагою w 21)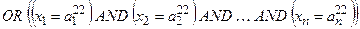 (з вагою w 22)
(з вагою w 22)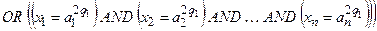 (з вагою
(з вагою 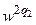 )
)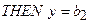
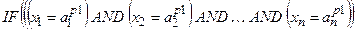 (з вагою wp 1)
(з вагою wp 1)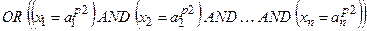 (з вагою w p 2)
(з вагою w p 2)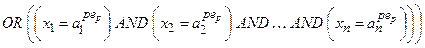 (з вагою
(з вагою 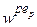 )
) (з вагою
(з вагою  )
)
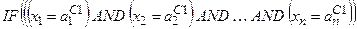 (з вагою wC 1)
(з вагою wC 1) (з вагою w С 2)
(з вагою w С 2)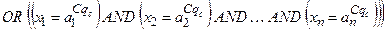 (з вагою
(з вагою 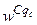 )
)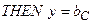 .
.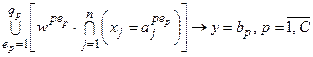 . (11.9)
. (11.9)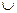 (OR) й
(OR) й 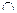 (AND); перелік цих об’єднаних правил при
(AND); перелік цих об’єднаних правил при  складає усю множину об’єднаних правил (11.8).
складає усю множину об’єднаних правил (11.8).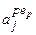 змінних
змінних 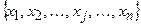 , які входять в логічні висловлювання (11.8), замінюють на відповідні функції належності
, які входять в логічні висловлювання (11.8), замінюють на відповідні функції належності 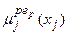 .
. , а логічне OR – знаком
, а логічне OR – знаком 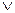 .
.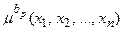 до даного терму вектора вхідних змінних
до даного терму вектора вхідних змінних  .
.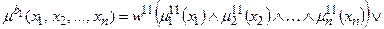

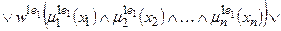
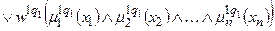 ;
;
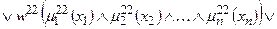
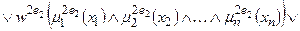
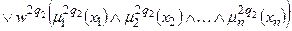 ;
; (11.10)
(11.10)

 ;
;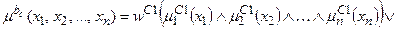
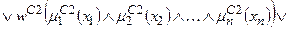
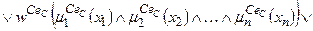
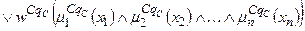 .
.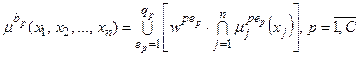 . (11.11)
. (11.11)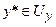 (чіткий числовий сигнал управління у* на універсумі Uy). При цьому на вхід блоку дефаззифікації можуть надходити два типи сигналів від блоку нечіткого логічного висновку:
(чіткий числовий сигнал управління у* на універсумі Uy). При цьому на вхід блоку дефаззифікації можуть надходити два типи сигналів від блоку нечіткого логічного висновку: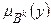 відповідної нечіткої множини
відповідної нечіткої множини 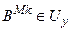 . Усього отримуємо N таких функцій належності – по загальній кількості правил. Усі вони безпосередньо передаються на дефаззифікатор. Числове значення виходу
. Усього отримуємо N таких функцій належності – по загальній кількості правил. Усі вони безпосередньо передаються на дефаззифікатор. Числове значення виходу 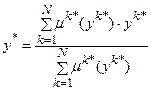 , (11.12)
, (11.12)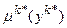 – розраховане числове значення функції належності μk (у) в точці yk* згідно відповідного правила.
– розраховане числове значення функції належності μk (у) в точці yk* згідно відповідного правила. Для двох правил (N =2) ідея методу показана на рис. 11.29, де рішення y* показане чорною точкою.
Для двох правил (N =2) ідея методу показана на рис. 11.29, де рішення y* показане чорною точкою. (11.13)
(11.13)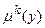 є неперервною.
є неперервною.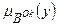 на відповідній нечіткій множині
на відповідній нечіткій множині 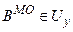 , і після цього дані передаються на дефаззифікатор. В цьому випадку числове значення сигналу управління
, і після цього дані передаються на дефаззифікатор. В цьому випадку числове значення сигналу управління 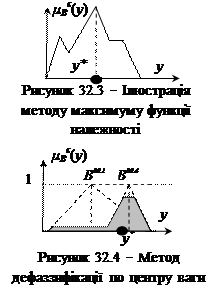 а)за методом максимуму функції належності, згідно з яким вихід нечіткої системи управління
а)за методом максимуму функції належності, згідно з яким вихід нечіткої системи управління  . (11.14)
. (11.14)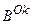 , бо функція належності
, бо функція належності  претендентів
претендентів 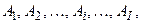
 за
за  критеріями
критеріями 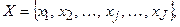
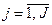 . Наприклад,
. Наприклад,  ,
,  – здатність розв’язувати задачі управління інформаційною безпекою;
– здатність розв’язувати задачі управління інформаційною безпекою; 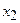 – виробничий досвід з інформаційних технологій,
– виробничий досвід з інформаційних технологій,  – досвід роботи з технічними засобами захисту інформації;
– досвід роботи з технічними засобами захисту інформації;  – досвід проведення комплексних досліджень захищеності приміщень;
– досвід проведення комплексних досліджень захищеності приміщень;  – досвід розробки КСЗІ.
– досвід розробки КСЗІ. як належність сукупності його характеристик до термів лінгвістичної змінної
як належність сукупності його характеристик до термів лінгвістичної змінної  . Наприклад,
. Наприклад,  , Р ={
, Р ={  =«не придатний»,
=«не придатний»,  =«задовільний»,
=«задовільний»,  =«умовно придатний»,
=«умовно придатний»,  =«придатний»,
=«придатний», 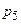 =«бездоганний»}. Кількість правил
=«бездоганний»}. Кількість правил  . Якщо кількість правил точно дорівнює
. Якщо кількість правил точно дорівнює  , то висновок щодо належності претендента до терму
, то висновок щодо належності претендента до терму  отримується за одним правилом, а якщо
отримується за одним правилом, а якщо  , то – за декількома. Універсумом лінгвістичної змінної P є інтервал
, то – за декількома. Універсумом лінгвістичної змінної P є інтервал  , на якому ФН нечітких множин
, на якому ФН нечітких множин  визначаються наступним чином
визначаються наступним чином  ;
;  ,
,  ;
;  ;
; 
 і правила мають вигляд:
і правила мають вигляд: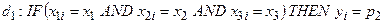 ;
; ;
; ;
; ;
; ;
; .
. : Якщо претендент має «здатність розв’язувати задачі управління інформаційною безпекою» і «виробничий досвід з інформаційних технологій», і «досвід роботи з технічними засобами захисту інформації», то він є «задовільний».
: Якщо претендент має «здатність розв’язувати задачі управління інформаційною безпекою» і «виробничий досвід з інформаційних технологій», і «досвід роботи з технічними засобами захисту інформації», то він є «задовільний». : Якщо претендент має «здатність розв’язувати задачі управління інформаційною безпекою» і «виробничий досвід з інформаційних технологій», і «досвід роботи з технічними засобами захисту інформації», і «досвід проведення комплексних досліджень захищеності приміщень», то він є «умовно придатний».
: Якщо претендент має «здатність розв’язувати задачі управління інформаційною безпекою» і «виробничий досвід з інформаційних технологій», і «досвід роботи з технічними засобами захисту інформації», і «досвід проведення комплексних досліджень захищеності приміщень», то він є «умовно придатний».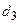 : Якщо претендент має «здатність розв’язувати задачі управління інформаційною безпекою» і «виробничий досвід з інформаційних технологій», і «досвід роботи з технічними засобами захисту інформації», і «досвід проведення комплексних досліджень захищеності приміщень», і «досвід розробки КСЗІ», то він є «бездоганний».
: Якщо претендент має «здатність розв’язувати задачі управління інформаційною безпекою» і «виробничий досвід з інформаційних технологій», і «досвід роботи з технічними засобами захисту інформації», і «досвід проведення комплексних досліджень захищеності приміщень», і «досвід розробки КСЗІ», то він є «бездоганний». : Якщо претендент має «здатність розв’язувати задачі управління інформаційною безпекою» і «виробничий досвід з інформаційних технологій», і «досвід роботи з технічними засобами захисту інформації», і «досвід розробки КСЗІ», то він є «придатний».
: Якщо претендент має «здатність розв’язувати задачі управління інформаційною безпекою» і «виробничий досвід з інформаційних технологій», і «досвід роботи з технічними засобами захисту інформації», і «досвід розробки КСЗІ», то він є «придатний». : Якщо претендент має дуже велику «здатність розв’язувати задачі управління інформаційною безпекою» і не має «виробничий досвід з інформаційних технологій», і має «досвід роботи з технічними засобами захисту інформації» і «досвід розробки КСЗІ», то він є «задовільний».
: Якщо претендент має дуже велику «здатність розв’язувати задачі управління інформаційною безпекою» і не має «виробничий досвід з інформаційних технологій», і має «досвід роботи з технічними засобами захисту інформації» і «досвід розробки КСЗІ», то він є «задовільний». : Якщо претендент не має «здатність розв’язувати задачі управління інформаційною безпекою» або не має «досвід роботи з технічними засобами захисту інформації», то він є «не придатний».
: Якщо претендент не має «здатність розв’язувати задачі управління інформаційною безпекою» або не має «досвід роботи з технічними засобами захисту інформації», то він є «не придатний». оцінюється на відповідність кожному критерію
оцінюється на відповідність кожному критерію  оцінками
оцінками  в межах інтервалу
в межах інтервалу  . Потім, використовуючи отримані
. Потім, використовуючи отримані  ,
,  в тому, що придатність претендента
в тому, що придатність претендента  ;
;  ;
;  ;
; ;
;  ;
;  .
. шляхом аналізу документів, тестування та співбесід визначено міри впевненості у їх відповідності критеріям
шляхом аналізу документів, тестування та співбесід визначено міри впевненості у їх відповідності критеріям