Нечіткі множини в системах керування

Вдалим застосуванням теорії нечітких множин є контролери нечіткої логіки. Їх функціонування дещо відрізняється від роботи звичайних контролерів; для опису системи замість диференційних рівнянь використовуються знання експертів. Ці знання можуть бути виражені за допомогою лінгвістичних змінних, які описані нечіткими множинами.

Загальна структура нечіткого мікроконтролера

Загальна структура мікроконтролера, що використовує нечітку логіку, показана на рис. Вона містить у своєму складі наступні складові:

· Блок фазіфікації.

· База знань.

· Блок рішень.

· Блок дефазіфікації.

Блок фазіфікації перетворює чіткі величини, які виміряні на виході об'єкта керування у нечіткі величини, що описані лінгвістичними змінними в базі знань.

Блок рішень використовує нечіткі умовні (if - then) правила, що закладено в базу знань, для перетворення нечітких вхідних даних в керуючі впливи, які мають також нечіткий характер.

Блок дефазіфікації перетворює нечіткі дані з виходу блоку рішень в чіткі величини, які використовуються для керування об'єктом.

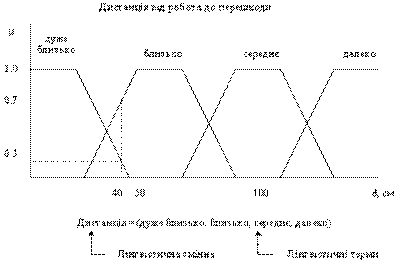
Рис. 1. Загальна структура нечіткого мікроконтролера

Всі системи з нечіткою логікою функціонують за одним принципом: показники вимірювальних приладів фазіфікуються (перетворюються в нечіткий формат), обробляються, дефазіфікуються й у вигляді звичайних сигналів подаються на виконавчі пристрої.

Розглянемо випадок керування мобільним роботом, задачею якого є об'їзд перешкод. Введемо дві лінгвістичні змінні: ДИСТАНЦІЯ (відстань від робота до перешкоди) і НАПРЯМОК (кут між подовжньою віссю робота та напрямком до перешкоди).

Розглянемо лінгвістичну змінну ДИСТАНЦІЯ. Значеннями її можна визначити терми ДАЛЕКО, СЕРЕДНЬО, БЛИЗЬКО і ДУЖЕ БЛИЗЬКО. Для фізичної реалізації лінгвістичної змінної необхідно визначити точні фізичні значення термів цієї змінної. Нехай змінна ДИСТАНЦІЯ може приймати будь-які значення з діапазону від нуля до нескінченності. Відповідно до теорії нечітких множин, в такому випадку кожному значенню відстані із зазначеного діапазону може бути поставлене у відповідність деяке число від нуля до одиниці, що визначає ступінь приналежності даної фізичної відстані (припустимо 40 см) до того чи іншого терму лінгвістичної змінної ДИСТАНЦІЯ.

Ступінь приналежності визначаємо функцією приналежності М(d), де d-відстань до перешкоди. В нашому випадку відстань 40 см. Можна задати ступінь приналежності до терму ДУЖЕ БЛИЗЬКО, що дорівнює 0,7, а до терму БЛИЗЬКО - 0,3 (рис. 2.). Конкретне визначення ступеня приналежності визначається експертами.

Рис. 2. Лінгвістична змінна і функція приналежності

Змінній НАПРЯМОК, яка може приймати значення в діапазоні від 0 до 360 градусів, задамо терми ВЛІВО, ПРЯМО і ВПРАВО.

Тепер необхідно задати вихідні змінні. У даному прикладі достатньо однієї, яку назвемо РУЛЬОВИЙ КУТ. Вона може містити терми: РІЗКО ВЛІВО, ВЛІВО, ПРЯМО, ВПРАВО, РІЗКО ВПРАВО. Зв'язок між входом та виходом запам'ятовується в таблиці нечітких правил.

Таблиця нечітких правил

Кожний запис в даній таблиці відповідає своєму нечіткому правилу, наприклад: Якщо дистанція близько і напрямок правий, тоді рульовий кут різко вліво

Таким чином, мобільний робот з нечіткою логікою буде працювати за наступним принципом: дані з сенсорів про відстань до перешкоди та напрямок до неї будуть фазіфіковані, оброблені згідно табличних правил, дефазіфіковані і отримані дані у вигляді керуючих сигналів надходять на приводи робота.

Переваги нечітких систем

· Можливість оперувати вхідними даними, заданими нечітко: наприклад, дані, які неперервно змінюються в часі (динамічні задачі), значення, що неможливо задати однозначно (результати статистичних опитувань, рекламні компанії);

· Можливість нечіткої формалізації критеріїв оцінки і порівняння: оперування критеріями "більшість", "можливе", переважно" тощо.;

· Можливість проведення якісних оцінок як вхідних даних, так і виведених результатів: значення даних, їх ступень достовірності (не плутати з імовірністю!) та її розподілом;

· Можливість проведення швидкого моделювання складних динамічних систем та їх порівняльний аналіз із заданим ступенем точності: оперуючи принципами поведінки системи, описаними fuzzy-методами:

o можна швидко з'ясувати точні значення змінних і скласти правила, що їх описують,

o можна оцінити різні варіанти вихідних значень.