Ідентифікація на основі моделі Мамдані

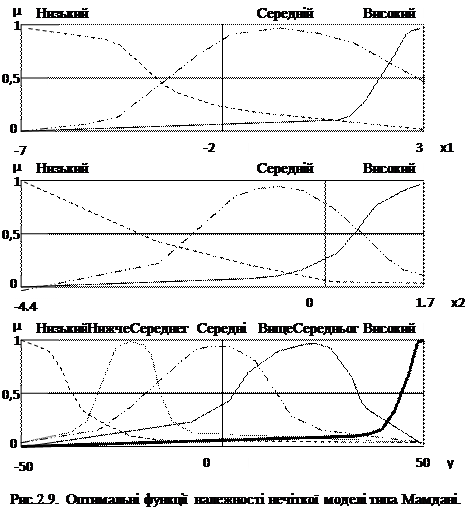
Входи і вихід моделі будемо розглядати як лінгвістичні змінні, значення яких визначаються з наступних термів-множин:

- для x₁ і x₂ - {«Низький», «Средний», «Высокий»};

- для у -{«Низкий», «Ниже Среднего», «Средний», «Выше Среднего», «Высокий»}.

Формализацію тер­мів виконаємо за симетричною гаусівською функцією надлежності (gaussmf):

,

де х — елемент універсальної множини;

h -параметр функції належності (координа­та максимума);

с — параметр функції надлежності (коефіцієнт концентрації).

Вибір такого типа функції надлежності пояснюється Ії простотою— вона задається лише двома параметрами, скорочує размірність задачі оптимі­зації на этапі параметричної ідентифікації.

В результаті візуального спостереження графі­ка ідентифікованої залежності, сформулюємо сім правил бази знань (табл. 1). На цьому етап структурної ідентифікації завершується.

 

 

 

Для проведення параметричної ідентифі­кації будемо використовувати програму, наведену в Придатку 2. Вона складається з m-cценарія, що викликає функцію нелінійної оптиміза­ції constr, і m-функції goal_fun, яка розраховує нев´язку при заданних значеннях керованих змінних. Кількість керованих змінних дорівнює шестнадцаті:

- одиннадцять коефіцієнтів концентрацій функцій належностей термів вхідних і вихідної змінних;

- дві координати максимумів центрів функцій належностей термів «Середний» вхід­ніх змінних;

- три координати максимумів центрів функцій належностей некрайніх термів вихідної змінної (тобто термів «Нижче Середнього», «Середній» і «Вище Середнього»). Коор­динати максимумів функцій належностей крайніх термів («Низький» та «Високий») не налагоджуються, тому що немає ніяких логичних міркувань, що вони будуть відрізнятись від границь диапазонів зміни змінних.

В результаті навчання знайдені оптимальні функції належності нечітких термів (рис. 2.9). Поверхня «входи-вихід», яка відповідає налагодженій нечіткої моделі типа Мамдані, показана на рис. 2.8, b. Нечітка модель оптимізована по навчальній виборці із 20 пар «входи-вихід». Средня квадратична похибка ідентифікації цієї моделі на контрольній виборці із 1000 точок складає 4.61.

 

Ідентифікація на основе моделі Сугено

По рис. 2.8, а візуально тящко оцінити кое­фіцієнти лінійних функцій, що пов´язують входи і вихід залежності (6) для конкретної підобласті. Тому базу знань згенеруемо безпосередньо з навчальної виборки. Навчальна выборка являє собою набор випадково згенерованих точок факторного про­стору, тому немає причин для використання кластеризації при синтезі бази знань. Бу­демо використовувати алгоритм решіточного разділу з параметрами по замовчуванню, — по два терми для оцінки кажної вхідної змінної с узагальненою дзвоноподібною функцією належності

 

де с — коефіцієнт концентрації функції належності; ν — коефіцієнт крутизни функції належності; h — координата мак­симума функції належності.

Пакет Fuzzy Logic Toolbox дозволяє синтезувати модель типу Сугено і навчити ії шляхом виклику однієї функції anfis в форматі:

fuzzy_model = anfis (traning_data, [],... number_of_iterations).

При навчанні налагоджувались 24 параметри нечіткої моделі — по 3 коефіцієнти в лінійній функції для кожного из 4-х правил бази знань і по 3 параметри для кожного з 4-х термів вхідних змінних. Така кількість налагоджуваних параметрів є мінімальною для нечіткої моделі типа Сугено з двома входами і одним виходом.

На рис. 2.8, бнаведена Поверхня «входи-вихід», що відповідає налагодженій нечіткій моделі типа Сугено. Нечітка модель оптимізована по навчальній виборці із 100 пар «вхо­ди—вихід». Середня квадратична похибка ідентифікації цієї моделі на контрольній виборці із 1000 точок складає 1.81. Графіки функцій належностей вхідних змінних показані на рис. 2.10; нечітка база знань для цієї моделі наведена в табл. 2.3.

 

 

Таблица 2 Нечітка база знань моделі типа Сугэно

Таблиця 2.3. Нечітка база знань моделі типу Сушеною

x1	x1	у
inlmfl	in2mfl	3.9 + 94.8 x1+696.2 x2
inlmfl	in2mf2	-1.8 + 118.6x1-249x2
inlmf2	in2mfl	0.7 -46.2 x1- 341.l x2
in1mf2	in2mf2	-0.6-58.5 x1+121.7х2