
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нечіткі моделі бази знань в системі matlabСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
[Штовба С. Д. Ідентифікація нелінійных зависимостей с помощью нечеткого логического вывода в системе MATLAB // Exponenta, #2/2003, c. 9 – 15].
В MatLab у пакеті Fuzzy Logic Toolbox реализовані два типи нечітких моделей (типа Мамдані і типа Сугэно), які відрізняються форматом бази знань та процедурою дефаззификації Модель типа Мамдані. В моделі типа Мамдані взаємний зв´язок між входами X = (x1,x2,...,xn) і выходом у визначається нечіткою базою знаньу вигляді сукупності логічних виразів: ЯКЩО (x1 =a1,j1) І (х2 =а2,j1) І...І (xn =an,j1) АБО (x1 =a1,j2) І (х2 =а2,j2) І...І (xn =an,j2) … АБО (x1 =a1,jkj) І (х2 =а2,jkj) І...І (xn =an,jkj) ТО y = dj, де i = n - загальна кількість змінних xi; j= m - загальна кількість лінгвістичних вихідних термів di для лінгвістичної оцінки вихідної змінної у(Х); jp = kj - загальна кількість рядків-кон´юнкцій для j-го правила, у якому вихід у оцінюється лінгвістичним термом di; аi,jp — лінгвістичний терм, яким оцінюється змінна xi в рядку з номером jp (p = За допомогою операцій
Введемо позначення: 1.
2.
3. Степень належності вхідного вектора X* = (х1*, х2*,... хn*) нечітким термам dj із бази знань (1) визначається наступною системою нечітких логічних рівнянь:
де Нечітка множина
де imp — імплікація (звичайно реализується як операція знаходження мінімума); agg — агрегировання нечітких множин (звичайно реализується як операція знаходження максимума). Чіткє значенння виходу у, відповідного вхідному вектору X*, визнчається в результаті дефаззифікації нечіткої множини
М одель типа Сугено (Sugeno) В моделі типа Сугено зв´язок між входами X = (х1, х2,... хn) та виходом у задається нечіткою базою знань у вигляді сукупності поліномів першої степені:
де b j,i — константи. База знань (3) аналогична системі логічних виразів (1) за вилученням висновків правил dj, які задаються не нечіткими термами, а чисельною лінійною функциею від входів:
Таким чином, база знань в моделі Сугено є гібридною — ії правила вміщують посилання у вигляді нечітких множин і висновок у вигляді чіткої лінійної функції. База знань (3) может трактуватись як розділ простору вхідних факторів на нечіткі підобласті, в кажній із яких значення функції відгуку розраховується як лінійна комбиінация входів. Правила є своєрідними перемикачами з одного лінійного закона «входи-вихід» на інший, теж лінійний. Границі підобластей розмиті, і тому одночасно можуть виконуватись кілька лінійних законів, але з різними вагами. Результуюче значенння виходу у визначається як суперпозиція лінійних залежностей для данної точки X* n-мірного факторного простору. Це може бути як середнє взважене
або як взважена сума
Значення Моделі типа Мамдані і типа Сугено будуть ідентичними, коли висновки правил задані чіткими числами, тобто у випадку, коли: 1) терми dj вихідної змінної в моделі типа Мамдані задаються синглтонами — нечіткими аналогами чітких чисел. В цьому випадку степені належності для усіх елементів універсальної множини дорівнюють нулю, за вилученням одного зі степеню належности равній одиниці; 2) висновки правил в базі знань моделі типу Сугено задані функціями, в яких усі коеффициєнти при вхідних змінних дорівнюють нулю.
|
||||
|
Последнее изменение этой страницы: 2016-06-24; просмотров: 590; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.45.82 (0.012 с.) |

 - порядковий номер змінної xi;
- порядковий номер змінної xi; - порядковий номер лінгвістичного вихідного терму di для лінгвістичної оцінки вихідної змінної у(Х);
- порядковий номер лінгвістичного вихідного терму di для лінгвістичної оцінки вихідної змінної у(Х);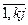 - порядковий номер рядка для j-го правила, у якому вихід у оцінюється лінгвістичним термом di;
- порядковий номер рядка для j-го правила, у якому вихід у оцінюється лінгвістичним термом di;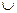 (АБО) і
(АБО) і 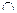 (І) нечітку базу знань перепишемо у більш компактному вигляді:
(І) нечітку базу знань перепишемо у більш компактному вигляді: (1)
(1) — функція належності входа хi нечіткому терму ai,jp. Тут i =
— функція належності входа хi нечіткому терму ai,jp. Тут i = 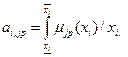
 .
. — функція належности вихода у до нечіткого терму dj, j=
— функція належности вихода у до нечіткого терму dj, j= 
 ;
; j=
j=  — операція із s-нормы (t-нормы), тобто із множини реализацій логічних операцій АБО (І). Найчастіше використовуються такі реалізації: для операції АБО — нахождення максимума, для операції І — нахождення мінімума.
— операція із s-нормы (t-нормы), тобто із множини реализацій логічних операцій АБО (І). Найчастіше використовуються такі реалізації: для операції АБО — нахождення максимума, для операції І — нахождення мінімума. , якавідповідає вхідному вектору X*, визначається наступним чином:
, якавідповідає вхідному вектору X*, визначається наступним чином:

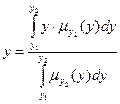 .
. , (3)
, (3) .
. ,
, .
. (X*) розраховується як і для моделі типу Мамдані, тобто за формулою (2). В моделі Сугено в якості операцій
(X*) розраховується як і для моделі типу Мамдані, тобто за формулою (2). В моделі Сугено в якості операцій 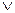 та
та  звичайно використовується відповідне ймовірносне АБО чи множення. В цьому випадку нечітка модель типа Сугено може розглядатись як особливий клас багатошарових нейронних мереж прямого розповсюдження сигнала, структура якої ізоморфна базі знань.Такі мережі отримали назву нейро-нечітких.
звичайно використовується відповідне ймовірносне АБО чи множення. В цьому випадку нечітка модель типа Сугено може розглядатись як особливий клас багатошарових нейронних мереж прямого розповсюдження сигнала, структура якої ізоморфна базі знань.Такі мережі отримали назву нейро-нечітких.


