
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Отримання висновку на нечіткій базі знань типу МамданіСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Формування нечіткої бази знань типу Мамдані На першому етапі проводиться структурна ідентифікація - формується нечітка база знань у вигляді сукупності лінгвістичних правил, які або задаються експертом, або отримуються з експериментальних даних. При цьому ми вважаємо, що визначені: універсуми вхідних і вихідних змінних; вектори нечітких множин, вектори лінгвістичних змінних та вектори функцій належності. Модуль нечіткого управління повинен моделювати невідому нам математичну залежність
де
Кожне правило складається з частини IF, яка зветься передумовою або антецедентом (англ. antecedent) і частини THEN, яка зветься наслідком або консеквентом (англ. consequent). Введення окремих позначень вхідних При виконанні подальших дій вважається: - якщо вхідна або вихідна змінна є якісною, то вона може бути використана в моделі, бо числові значення факторів все одно замінюються на якісні показники у вигляді термів; - виходи
{з вагою де вагові коефіцієнти - загальний висновок отримується за окремим правилом, в якому висновки з усіх правил Rk і вхідні дані Правила у вигляді (11.7) та відповідні їм логічні вирази часто використовуються у фаховій літературі при розгляді загальних питань, але практикою встановлено, що багато правил мають однаковий вихід. Такі правила доцільно об’єднувати, отримуючи тим самим об’єднані правила з однаковим загальним виходом. Тоді замість нумерації правил за верхніми індексами - - - Після замін k на pеp кожне правило використовується з відповідною вагою Базу нечітких знань виконують у вигляді таблиці (табл.32.1), яка відповідає таким вимогам:
1. В рядках записуються правила за їх порядковими номерами р та ер (або за номером - одна колонка - номера рядка правила pеp; - n колонок - позначення термів вхідних змінних - одна колонка - ваговий коефіцієнт - одна колонка виходу у - позначення термів вихідних змінних. Таким чином, розмірність таблиці дорівнює 2. Комірки таблиці, які відповідають колонкам входів 3. На початку роботи системи вважають усі ваги 4. Отриману базу знань перевіряють на наявність тотожних та протилежних за змістом рядків. База знань відображує знання у вигляді логічних висловлювань типу IF … THEN …, OR, які пов’язують значення вхідних змінних
OR …
ELSE
OR …
ELSE
OR …
OR …
ELSE (11.8)
OR …
Подібну систему логічних висловлень, яку називають нечіткою базою знань, можна компактно записати як
Тут записане одне р -те об’єднане логічне висловлювання із (11.8) з використанням операцій Таким чином, невідома залежність Y=F(X) формально замінюється нечіткими логічними висловлюваннями (11.9), які базуються на створеній експертом матриці знань табл. 11.5. Формування системи нечітких логічних рівнянь для моделі Мамдані Для отримання висновку за Мамдані при формуванні системи нечітких логічних рівнянь система логічних висловлювань (11.9) перетворюється наступним чинам: 1. Вхідні лінгвістичні оцінки (терми) 2. Вагові коефіцієнти 3. Логічне AND замінюється знаком 4. Вихідна лінгвістична оцінка (терм bр) змінної виходу у замінюється відповідною функцією належності В результаті отримуємо систему логічних рівнянь:
………………………………………………………
………………………………………………………
………………………………………………………
………………………………………………………
…………………………………………………………………………….
………………………………………………………
………………………………………………………
…………………………………………………………………………….
………………………………………………………
………………………………………………………
За аналогією з (11.9) систему логічних рівнянь (11.10) можна компактно записати як
Тут записане одне р -те об’єднане логічне рівняння із (11.10) з використанням операцій Таким чином, невідома нам залежність Y=F(X) формально замінюється нечіткими логічними рівняннями (11.11), які базуються на створеній експертом матриці знань табл.11.5. Робота блоку дефаззифікації при отриманні висновку за моделлю Мамдані Основне призначення блоку дефаззифікації – видати на виході нечіткої системи управління числовий сигнал виходу 1. Блок нечіткого логічного висновку для кожного k– ого правила бази нечітких знань визначає вигляд вихідної функції належності а) метод дефаззифікації по середньому центру (англ.. center average defuzzification), за яким числове значення у* розраховується за формулою
де yk* - точка у вигляді числового значення, в якій функція належності μk(у) отримує максимальне числове значення на універсумі виходу Uy;
Перевагою методу є те, що отримане рішення у вигляді числа не залежить від форми функції μk (у) та нечіткої множини
б) метод дефаззифікації по сумі центрів (англ.. center of sums defuzzification), за яким числове значення у* розраховується по величинам інтегралів
Цей метод може використовуватися, якщо ФН 2. Блок нечіткого логічного висновку об’єднує висновки усіх правил: вихідні дані
б) за методом центру тяжіння (центру ваги, центру площини) (англ.. center of gravity method, center of area method), згідно з яким вихід нечіткої системи управління
Цей метод є найбільш розповсюдженим. Тут інтегрування по у може розглядатись у як у межах всього універсуму Uy, так і в межах носія НМ
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-24; просмотров: 443; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.194.225 (0.01 с.) |

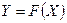 , де
, де 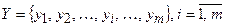 – вектор оптимальних виходів (вектор функцій мети), а
– вектор оптимальних виходів (вектор функцій мети), а 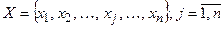 – вектор вхідних змінних, сукупністю логічних висловлень IF-THEN, яка грубо (дискретно) відображає шляхом апроксимації зв´язок між входами та виходами і має вигляд нечітких лінгвістичних правил
– вектор вхідних змінних, сукупністю логічних висловлень IF-THEN, яка грубо (дискретно) відображає шляхом апроксимації зв´язок між входами та виходами і має вигляд нечітких лінгвістичних правил 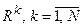 , де
, де 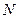 – загальна кількість правил, у вигляді:
– загальна кількість правил, у вигляді: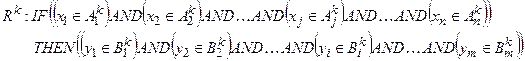 (11.6)
(11.6)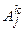 – терми лінгвістичних змінних вхідних даних для k -го правила, які нумеруються окремо для кожного k –ого правила і стосуються вхідної числової змінної xj;
– терми лінгвістичних змінних вхідних даних для k -го правила, які нумеруються окремо для кожного k –ого правила і стосуються вхідної числової змінної xj;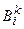 – терми лінгвістичних змінних вихідних даних для k -ого правила, які нумеруються окремо для кожного k –го правила і стосуються вихідної числової змінної уі.
– терми лінгвістичних змінних вихідних даних для k -ого правила, які нумеруються окремо для кожного k –го правила і стосуються вихідної числової змінної уі.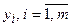 є взаємно незалежними, тому можна використовувати правила (11.6) лише для одного виходу:
є взаємно незалежними, тому можна використовувати правила (11.6) лише для одного виходу: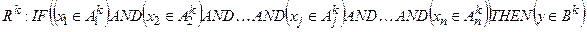
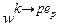 }, (11.7)
}, (11.7)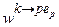 відображують впевненість експерта щодо впливу правила на роботу системи;
відображують впевненість експерта щодо впливу правила на роботу системи;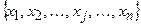 виступають як складові антецеденту і пов’язані між собою оператором OR.
виступають як складові антецеденту і пов’язані між собою оператором OR.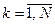 використовується нумерація з подвійними верхніми індексами заміною k на pеp, де:
використовується нумерація з подвійними верхніми індексами заміною k на pеp, де: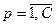 – порядковий номер об’єднаних правил: кілька правил з однаковим виходом bp об’єднуються в одне об’єднане правило навколо вихідного терму bp. Тому при заповненні таблиці спочатку групують правила, що мають однакові терми виходу,в об’єднані правила;
– порядковий номер об’єднаних правил: кілька правил з однаковим виходом bp об’єднуються в одне об’єднане правило навколо вихідного терму bp. Тому при заповненні таблиці спочатку групують правила, що мають однакові терми виходу,в об’єднані правила;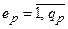 – порядковий номер правила в р -ому об’єднаному правилі для вихідного терму bp;
– порядковий номер правила в р -ому об’єднаному правилі для вихідного терму bp;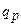 – загальна кількість правил в р -ому об’єднаному правилі для вихідного терму bp.
– загальна кількість правил в р -ому об’єднаному правилі для вихідного терму bp. .
.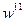
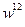
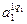
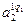
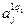
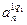
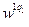
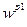

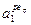
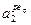
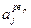

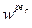


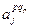
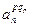
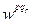
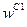
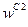
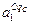
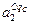

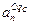

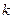 ). Загальна кількість рядків дорівнює
). Загальна кількість рядків дорівнює 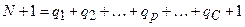 (один рядок додано для заголовків колонок). Загальна кількість колонок таблиці дорівнює (n+3):
(один рядок додано для заголовків колонок). Загальна кількість колонок таблиці дорівнює (n+3):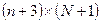 .
.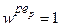 . Потім їх значення уточнюють в процесі накопичення даних експериментів. Вагові коефіцієнти
. Потім їх значення уточнюють в процесі накопичення даних експериментів. Вагові коефіцієнти  (з вагою w 11)
(з вагою w 11)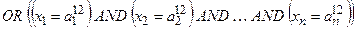 (з вагою w 12)
(з вагою w 12)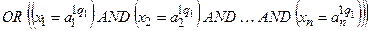 (з вагою
(з вагою  )
)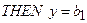
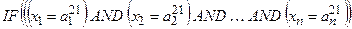 (з вагою w 21)
(з вагою w 21)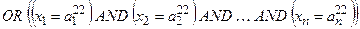 (з вагою w 22)
(з вагою w 22)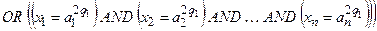 (з вагою
(з вагою 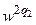 )
)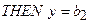
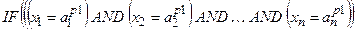 (з вагою wp 1)
(з вагою wp 1)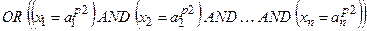 (з вагою w p 2)
(з вагою w p 2)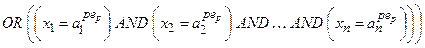 (з вагою
(з вагою 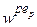 )
) (з вагою
(з вагою  )
)
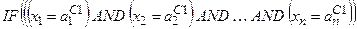 (з вагою wC 1)
(з вагою wC 1) (з вагою w С 2)
(з вагою w С 2)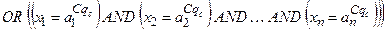 (з вагою
(з вагою 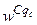 )
)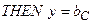 .
.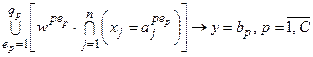 . (11.9)
. (11.9)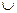 (OR) й
(OR) й 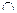 (AND); перелік цих об’єднаних правил при
(AND); перелік цих об’єднаних правил при  складає усю множину об’єднаних правил (11.8).
складає усю множину об’єднаних правил (11.8).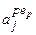 змінних
змінних 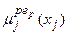 .
. , а логічне OR – знаком
, а логічне OR – знаком 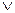 .
.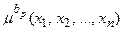 до даного терму вектора вхідних змінних
до даного терму вектора вхідних змінних  .
.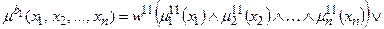

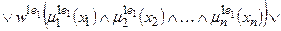
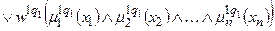 ;
;
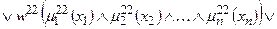
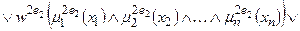
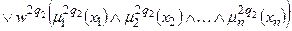 ;
; (11.10)
(11.10)

 ;
;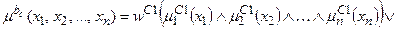
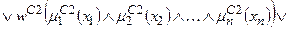
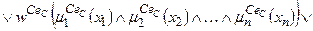
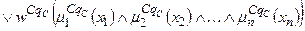 .
.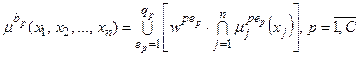 . (11.11)
. (11.11)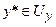 (чіткий числовий сигнал управління у* на універсумі Uy). При цьому на вхід блоку дефаззифікації можуть надходити два типи сигналів від блоку нечіткого логічного висновку:
(чіткий числовий сигнал управління у* на універсумі Uy). При цьому на вхід блоку дефаззифікації можуть надходити два типи сигналів від блоку нечіткого логічного висновку: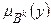 відповідної нечіткої множини
відповідної нечіткої множини 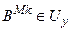 . Усього отримуємо N таких функцій належності – по загальній кількості правил. Усі вони безпосередньо передаються на дефаззифікатор. Числове значення виходу
. Усього отримуємо N таких функцій належності – по загальній кількості правил. Усі вони безпосередньо передаються на дефаззифікатор. Числове значення виходу 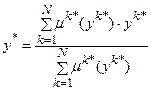 , (11.12)
, (11.12)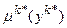 – розраховане числове значення функції належності μk (у) в точці yk* згідно відповідного правила.
– розраховане числове значення функції належності μk (у) в точці yk* згідно відповідного правила. Для двох правил (N =2) ідея методу показана на рис. 11.29, де рішення y* показане чорною точкою.
Для двох правил (N =2) ідея методу показана на рис. 11.29, де рішення y* показане чорною точкою. (11.13)
(11.13)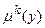 є неперервною.
є неперервною.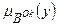 на відповідній нечіткій множині
на відповідній нечіткій множині 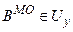 , і після цього дані передаються на дефаззифікатор. В цьому випадку числове значення сигналу управління
, і після цього дані передаються на дефаззифікатор. В цьому випадку числове значення сигналу управління 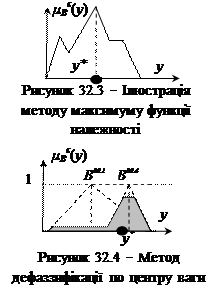 а)за методом максимуму функції належності, згідно з яким вихід нечіткої системи управління
а)за методом максимуму функції належності, згідно з яким вихід нечіткої системи управління  . (11.14)
. (11.14)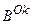 , бо функція належності
, бо функція належності 


