Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Отримання висновку на нечіткій базі знань типу Такагі – СугеноСодержание книги
Поиск на нашем сайте
Формування нечіткої бази знань типу Такагі – Сугено Розглянута модель Мамдані використовує нечітку базу правил, в яких частини IF та THEN мають нечіткий характер. В моделі Такагі-Сугено правила мають нечіткий характер лише в розділі IF, а в розділі THEN вони містять чіткі функціональні залежності від вхідних змінних
OR …
OR …
У лінійному випадку вихід р -ого об’єднаного правила можна записати у вигляді
де b 0, b 1, b 2, …, bn – деякі постійні коефіцієнти. Подібну систему логічних висловлень, яку називають нечіткою базою знань моделі Такагі-Сугено, можна компактно записати як
Формування системи нечітких логічних рівнянь для моделі Такагі-Сугено З нечітких правил (11.16) отримуємо відповідну систему логічних виразів:
……………………………………………………… (11.17)
………………………………………………………
Систему логічних виразів (11.17) компактно можна записати у вигляді
Отримана система логічних виразів Такагі-Сугено (11.18) аналогічна системі логічних рівнянь (11.10) за винятком отримуваного висновку, який відповідає консеквентам відповідних правил і задається не нечіткими термами, а жорсткою функціональною залежністю, наприклад, лінійною залежністю, від входів. Таким чином, ліва частина логічного виразу (11.18) для деякого р -ого об’єднаного правила діє наче перемикач, що ставить у відповідність заданій сукупності нечітких множин входу (тобто заданій нечіткій підобласті існування виходу) однозначну чітку функцію виходу, визначену з експериментальних даних або з досвіду експерта. Таким чином, база знань моделі типу Такагі-Сугено є гібридною: посилки її правил використовують нечіткі множини, а висновок має вигляд чіткої лінійної функції. Оскільки області існування чіткої функції виходу є розмитими, то чіткий числовий результат виходу у* визначається як суперпозиція рішень ряду об’єднаних правил. Моделі типу Мамдані та типу Такагі-Сугено стають ідентичними, якщо в моделі Мамдані вихідні терми задаються синглтонами (нечіткими аналогами чітких чисел), а в моделі типу Такагі-Сугено вихідна функція являє собою ті ж самі постійні числа (при цьому усі коефіцієнти при змінних дорівнюють нулю).
Розглянемо приклад модуля управління Такагі – Сугено. База правил, яка видає сигнал управління на поворотний пристрій відеокамери містить два правила
де
Відповідні функції належності моделі наведені на рис. 11.32. Вважаємо, що на вхід подані змінні із заданими числовими значеннями Із рис. 11.32 для З кожного правила розраховується відповідна ФН у вигляді
Крім того,
МНОГОКРИТЕРИАЛЬНЫЙ ВЫБОР АЛЬТЕРНАТИВ С ИСПОЛЬЗОВАНИЕМ МЕТОДА НЕЧЕТКОГО ВЫВОДА Океания И.Г., Филиппов А.В. Кременчугский университет экономики, информационных технологий и управления. Задача прийняття рішень - одна з найпоширеніших в будь-якій предметній області. Її рішення зводиться до вибору однієї або декількох кращих альтернатив з деякого набору. Для того, щоб зробити такий вибір, необхідно чітко визначити мету та критерії (показники якості), за якими буде проводитися оцінка деякого набору альтернативних варіантів. Вибір методу вирішення такого завдання залежить від кількості і якості доступної інформації. Дані, необхідні для здійснення обґрунтованого вибору, можна розділити на чотири категорії: інформація про альтернативні варіанти, інформація про критерії вибору, інформація про уподобання, інформація про оточення завдання. З множини відомих методів і підходів до прийняття рішень найбільший інтерес представляють ті, які дають можливість враховувати багатокритеріальність і невизначеність, а також дозволяють здійснювати вибір рішень з множин альтернатив різного типу при наявності критеріїв, що мають різні типи шкал вимірювання. Одним з таких методів є метод багатокритеріального вибору альтернатив на основі композиційного правила агрегування альтернатив з інформацією про уподобання особи, що приймає рішення, які задані у вигляді нечітких суджень.
Як приклад розглянемо задачу вибору співробітника служби безпеки з Придатність претендента на посаду оцінюється за системою правил Наприклад,
В словесній формі ці правила мають наступний вигляд:
Спочатку кожний претендент
Припустимо, що для п’яти претендентів
Нехай U - множина елементів, А - її нечітка підмножина, ступінь належності елементів до якої є числом з одиничного інтервалу [0, 1]. Елементи підмножини А є значеннями лінгвістичної змінної X. Припустимо, що множина рішень характеризується набором критеріїв xj, х 2,..., xn, тобто лінгвістичних змінних, заданих на базових множинах Uj, U 2,..., Un. Набір з декількох критеріїв з відповідними значеннями ФН характеризує уявлення особи, що приймає рішення, про якість альтернативи. Для осмислення задовільності кожної з альтернатив застосуємо правило композиційного виведення Е, = G, ° D, де Е, - ступінь задоволення альтернативи до, G, - відображення альтернативи до у вигляді нечіткого підмножини на U, D - загальне функціональне рішення. Тоді /(а(.*) = тах (ГШП (/ (а (і), кол (і))). Зіставлення альтернатив відбувається на основі точкових оцінок. Для нечіткої множини С з 1 визначаємо а- уровневое множина (<Х? [0, 1]) С "= {и | / ІЕ (і) га, іє7}. Кращою вважається альтернатива з найбільшим значенням точкової оцінки. Операції перетину нечітких множин відповідає знаходження мінімуму їх функцій належності де V = UlxU2x... xUp, v = (ul, u1,..., up), iiA (Uj) -значення функції приналежності елемента ut нечіткій множині Аг Для додання спільності судженням позначимо базові множини І / і Гчерез Ж Тоді А - нечітке підмножина W, в той час як В-нечітке підмножина одиничного інтервалу І. Для представлення правил використовується операція імплікації, для якої запропоновані різні способи нечіткої реалізації, наприклад, нечітка імплікація Лукасевича у вигляді / (ц (№, /) = тіп (і, (й-, ід (і>))) Висловлювання di, d1,..., ^ перетворюються в нечіткі множини Н,, Ні,..., НЧ- Їх перетином є множина П.... пН (і для кожного (w, i) eWxf Розглянутий метод прийняття рішень з використанням правил нечіткого виводу є адаптацією нечіткої логіки до процесів прийняття рішень з вихідними даними у вигляді точкових оцінок.
Из множества известных методов и подходов к принятию решений наибольший интерес представляют те, которые дают возможность учитывать многокритериальность и неопределенность, а также позволяют осуществлять выбор решений из множеств альтернатив различного типа при наличии критериев, имеющих разные типы шкал измерения. В рамках данной работы рассматривается метод многокритериального выбора альтернатив на основе композиционного правила агрегирования альтернатив с информацией о предпочтениях лица, принимающего решение, которые заданы в виде нечетких суждений.
Пусть U — множество элементов, А - его нечеткое подмножество, степень принадлежности элементов к которому есть число из единичного интервала [0, 1]. Элементы подмножества А являются значениями лингвистической переменной X, Допустим, что множество решений характеризуется набором критериев xj, х2,...,*„ т.е. лингвистических переменных, заданных на базовых множествах и;, ц^,.., щ соответственно. Набор из нескольких критериев с соответствующими значениями характеризует представление лица, принимающего решение, об удовлетворительности альтернативы. Операции пересечения нечетких множеств соответствует нахождение минимума их функций принадлежности
где V = UlxU2x...xUp,v = (ul,u1,...,up),iiA (Uj) -значение функции принадлежности элемента ut нечеткому множеству Аг Для придания общности суждениям обозначим базовые множества І/ и Гчерез Ж Тогда А - нечеткое подмножество W, в то время как В-
нечеткое подмножество единичного интервала І. Для представления правил используется операция импликации, для которой предложены различные способы нечеткой реализации, например, нечеткая импликация Лукасевича в виде /(ц(№,/)=тіп(і,(і-,ид(и>)))
Высказывания di,d1,..., ^преобразуются в нечеткие множества
Н,,Ні,...,НЧ- Их пересечением является множество П....пН(и для каждого (w,i)eWxf
Для осмысления удовлетворительности каждой из альтернатив применим правило композиционного вывода Е, = G, ° D, где Е, - степень удовлетворения альтернативы к, G, - отображение альтернативы к в виде нечеткого подмножества на U, D - общее функциональное решение. Тогда /(а(.*) = тах(гшп(/(а(и), цв(и))). Сопоставление альтернатив
происходит на основе точечных оценок. Для нечеткого множества С с 1 определяем а- уровневое множество (<Х? [0, 1]) С„ ={і|/іе(і)га,іє7}. Лучшей считается альтернатива с наибольшим значением точечной оценки. Рассмотренный метод принятия решений с использованием правил нечеткого вывода является адаптацией нечеткой логики к процессам принятия решений с исходными данными в виде точечных оценок.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-24; просмотров: 435; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.206.240 (0.01 с.) |

 . Для деякого р -ого об’єднаного правила з виходом yр застосовується логічне висловлювання
. Для деякого р -ого об’єднаного правила з виходом yр застосовується логічне висловлювання (з вагою wp 1)
(з вагою wp 1)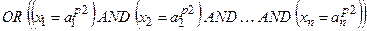 (з вагою wp 2)
(з вагою wp 2)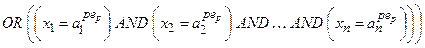 (з вагою
(з вагою 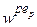 ) (11.15)
) (11.15) (з вагою
(з вагою  )
)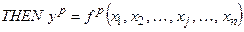 .
.  ,
, , (11.16)
, (11.16)


 .
.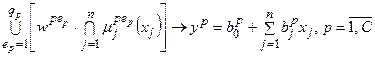 . (11.18)
. (11.18)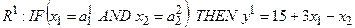 ;
; ,
, =«Повільно»,
=«Повільно»,  =«Швидко» - терми лінгвістичної змінної «Швидкість пересування об’єкта»={«Повільно», «Швидко»};
=«Швидко» - терми лінгвістичної змінної «Швидкість пересування об’єкта»={«Повільно», «Швидко»}; =«Малий»,
=«Малий»,  =«Середній» - терми лінгвістичної змінної «Відносний розмір об’єкта в кадрі»={«Малий», «Середній», «Великий»}.
=«Середній» - терми лінгвістичної змінної «Відносний розмір об’єкта в кадрі»={«Малий», «Середній», «Великий»}. . Необхідно визначити
. Необхідно визначити  - числовий вихід системи управління.
- числовий вихід системи управління. ;
;  ;
;  ;
;  .
. . У даному випадку:
. У даному випадку:
 .
. ;
; .
. В результаті використання формули (11.21) отримуємо
В результаті використання формули (11.21) отримуємо  .
. претендентів
претендентів 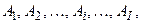
 за
за  критеріями
критеріями 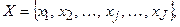
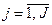 . Наприклад,
. Наприклад,  ,
,  – здатність розв’язувати задачі управління інформаційною безпекою;
– здатність розв’язувати задачі управління інформаційною безпекою; 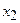 – виробничий досвід з інформаційних технологій,
– виробничий досвід з інформаційних технологій,  – досвід роботи з технічними засобами захисту інформації;
– досвід роботи з технічними засобами захисту інформації;  – досвід проведення комплексних досліджень захищеності приміщень;
– досвід проведення комплексних досліджень захищеності приміщень;  – досвід розробки КСЗІ.
– досвід розробки КСЗІ. як належність сукупності його характеристик до термів лінгвістичної змінної
як належність сукупності його характеристик до термів лінгвістичної змінної  . Наприклад,
. Наприклад,  , Р ={
, Р ={  =«не придатний»,
=«не придатний»,  =«задовільний»,
=«задовільний»,  =«умовно придатний»,
=«умовно придатний»,  =«придатний»,
=«придатний», 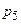 =«бездоганний»}. Кількість правил
=«бездоганний»}. Кількість правил  . Якщо кількість правил точно дорівнює
. Якщо кількість правил точно дорівнює  , то висновок щодо належності претендента до терму
, то висновок щодо належності претендента до терму  отримується за одним правилом, а якщо
отримується за одним правилом, а якщо  , то – за декількома. Універсумом лінгвістичної змінної P є інтервал
, то – за декількома. Універсумом лінгвістичної змінної P є інтервал  , на якому ФН нечітких множин
, на якому ФН нечітких множин  визначаються наступним чином
визначаються наступним чином  ;
;  ,
,  ;
;  ;
; 
 і правила мають вигляд:
і правила мають вигляд: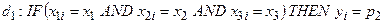 ;
; ;
; ;
; ;
; ;
; .
. : Якщо претендент має «здатність розв’язувати задачі управління інформаційною безпекою» і «виробничий досвід з інформаційних технологій», і «досвід роботи з технічними засобами захисту інформації», то він є «задовільний».
: Якщо претендент має «здатність розв’язувати задачі управління інформаційною безпекою» і «виробничий досвід з інформаційних технологій», і «досвід роботи з технічними засобами захисту інформації», то він є «задовільний». : Якщо претендент має «здатність розв’язувати задачі управління інформаційною безпекою» і «виробничий досвід з інформаційних технологій», і «досвід роботи з технічними засобами захисту інформації», і «досвід проведення комплексних досліджень захищеності приміщень», то він є «умовно придатний».
: Якщо претендент має «здатність розв’язувати задачі управління інформаційною безпекою» і «виробничий досвід з інформаційних технологій», і «досвід роботи з технічними засобами захисту інформації», і «досвід проведення комплексних досліджень захищеності приміщень», то він є «умовно придатний».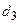 : Якщо претендент має «здатність розв’язувати задачі управління інформаційною безпекою» і «виробничий досвід з інформаційних технологій», і «досвід роботи з технічними засобами захисту інформації», і «досвід проведення комплексних досліджень захищеності приміщень», і «досвід розробки КСЗІ», то він є «бездоганний».
: Якщо претендент має «здатність розв’язувати задачі управління інформаційною безпекою» і «виробничий досвід з інформаційних технологій», і «досвід роботи з технічними засобами захисту інформації», і «досвід проведення комплексних досліджень захищеності приміщень», і «досвід розробки КСЗІ», то він є «бездоганний». : Якщо претендент має «здатність розв’язувати задачі управління інформаційною безпекою» і «виробничий досвід з інформаційних технологій», і «досвід роботи з технічними засобами захисту інформації», і «досвід розробки КСЗІ», то він є «придатний».
: Якщо претендент має «здатність розв’язувати задачі управління інформаційною безпекою» і «виробничий досвід з інформаційних технологій», і «досвід роботи з технічними засобами захисту інформації», і «досвід розробки КСЗІ», то він є «придатний». : Якщо претендент має дуже велику «здатність розв’язувати задачі управління інформаційною безпекою» і не має «виробничий досвід з інформаційних технологій», і має «досвід роботи з технічними засобами захисту інформації» і «досвід розробки КСЗІ», то він є «задовільний».
: Якщо претендент має дуже велику «здатність розв’язувати задачі управління інформаційною безпекою» і не має «виробничий досвід з інформаційних технологій», і має «досвід роботи з технічними засобами захисту інформації» і «досвід розробки КСЗІ», то він є «задовільний». : Якщо претендент не має «здатність розв’язувати задачі управління інформаційною безпекою» або не має «досвід роботи з технічними засобами захисту інформації», то він є «не придатний».
: Якщо претендент не має «здатність розв’язувати задачі управління інформаційною безпекою» або не має «досвід роботи з технічними засобами захисту інформації», то він є «не придатний». оцінюється на відповідність кожному критерію
оцінюється на відповідність кожному критерію  оцінками
оцінками  в межах інтервалу
в межах інтервалу  . Потім, використовуючи отримані
. Потім, використовуючи отримані  ,
,  в тому, що придатність претендента
в тому, що придатність претендента  ;
;  ;
;  ;
; ;
;  ;
;  .
. шляхом аналізу документів, тестування та співбесід визначено міри впевненості у їх відповідності критеріям
шляхом аналізу документів, тестування та співбесід визначено міри впевненості у їх відповідності критеріям