
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Переваги використання нечіткої логіки
Оператори нечіткої логіки дуже схожі зі звичайними булевыми операторами. Функції належності і правила нечіткої логіки, піддані лінгвістичної модифікації, дозволяють значно розширити можливості системних операторів. Розроблювачі можуть набагато спростити складність систем, використовуючи нечітку логіку, оскільки вона дозволяє моделювати комплексні програми з великою кількістю входів і виходів. За допомогою нечіткої логіки можна домогтися зниження системних вимог, а виходить, скоротити витрати на апаратні засоби. У багатьох випадках складне математичне моделювання переважніше замінити функціями належності і правилами нечіткої логіки і з їхньою допомогою керувати системою. При скороченні обсягів інформації розміри коду зменшуються, тому система працює швидше. Крім того, це дозволяє використовувати менш зроблені апаратні засоби.
Інші області застосування Нечітка логіка використовується в найрізноманітніших додатках. Найбільш очевидна область її застосування - системи керування, яким нечітка' логіка вже забезпечили комерційний успіх. Нечітка логіка використовується в пристрої відеокамер і фотоапаратів з автофокусом, системах змішування це- -мента, автомобільних системах (наприклад, системах АБС) і навіть системах, заснованих на правилах. Напевно, самі корисні області застосування усе ще залишаються неизвест-' ными. Сама назва «нечітка логіка» не вселяє особливої довіри, хоча давно I відомо, що це надійний метод. Як і багато інших методик ИИ, нечітка логіка в даний час усі частіше використовується в пристроях повсякденного застосування, де вона більше не асоціюється зі штучним інтелектом. Деякі з методів Врахуванняу недетермірованності були приведені при розгляді продукційних систем (пошук в глибину, пошук в ширину, принцип метапродукцій і т.д.). Отримання висновку в логіці У логіці використовуються два загальних методи отримання висновків: дедукція та індукція. Деду́кція — процес виведення висновку, що гарантовано випливає, якщо вхідні припущення істинні то висновок на їх підставі є чинним (дійсним, правильним). Висновок повинен базуватись винятково на основі попередньо наведених доказів, аксіом, постулатів, законів та не повинен містити нової інформації про предмет, що досліджується. Дедукція була вперше описана у працях давньогрецьких філософів, таких як Аристотель. Процес виведення дедуктивно правильний тоді і лише тоді, коли з точки зору логіки за умови істинності вхідних припущень висновки також істинні, тобто логічно неможливі хибні висновки за правильних припущень.
Дедукційна система Інду́кція — це процес судження, котрий досягає висновку, що при наявному стані знань є напевно істинний, але не гарантує його. Індуктивний висновок може бути спростований або узагальнений при наявності додаткових фактів. Інакше, індукція полягає у формулюванні закону, ґрунтуючись на обмеженому об'ємі спостережень повторюваних подій. Прикладами індуктивних висновків є, наприклад, такі пари спостереження/висновок: - Цей лебідь білий. - Всі лебеді білі. Головною відмінністю індукції є те що для її застосування не вимагається знати усі факти до того як зробити висновок. Оскільки на практиці неможливо з'ясувати все перед тим як робити умовивід, дедукція не має широкого застосування у реальному світі, окрім математики й природничих наук, які використовують математичні методи. Індукція, натомість, оперує набором неповних фактів, та на їх основі робить висновок який напевно випливає, не даючи жодних гарантій щодо його істинності. Попри це, індукція дає можливість набувати нових знань, котрі не є очевидними при розгляді вихідних тверджень. Часто зустрічається помилкова думка, що дедукція рухається від загального до окремого та що індукція - це рух у зворотному напрямку. Деякі філософи вважають термін «індуктивна логіка» непорозумінням, оскільки істинність індуктивного висновку не залежить від законів формальної логіки, котрі є за означенням дедуктивними. На противагу дедукції, індуктивні висновки не мають того ж ступеня достовірності що і вихідні твердження. Наприклад, у наведеному вище прикладі висновок про те що всі лебеді білі міг вважатись істинним у Європі поки не було відкрито Австралію. Індуктивне судження ніколи не є зобов'язуючим, але є обґрунтованим. Індуктивне судження є також дедуктивно некоректним. Проблема індукції, що полягає у пошуку обґрунтування індуктивного судження, вперше була формально розглянута Давидом Юмом.
Виокремлюють різні типи індуктивного судження: - передбачення; - узагальнення; - за аналогією; - посилання на авторитет; - причинно-наслідкове. Для раціонального обґрунтування індукції використовується Байєсівський вивід Теорема Байєса використовується для обчислення ступеня довіри до гіпотези при отриманні нових фактів. Modus ponens
Modus ponens (Латиною: метод що підтверджує) це коректна, проста форма аргументації (інколи використовується скорочення MP): Якщо P, то Q. P. Звідси Q. або у логіко-операторному записі:
де Приклад твердження у формі modus ponens: Якщо демократія є найкращою системою урядування, то кожен повинен голосувати. Демократія є найкращою системою урядування. Отже, кожен повинен голосувати. Той факт, що вивід є коректним не ґарантує істиності вихідних тверджень. Коректність modus ponens каже нам тільки те, що висновок є істинним тоді і тільки тоді, коли всі вихідні твердження є істинними. Слід нагадати, що коректний логічний вивід, у якому одне або більше вихідних тверджень не є істинними, називають необґрунтованим, інакше, якщо усі твердження є істинними, такий аргумент називають обґрунтованим. У більшості логічних систем Modus ponens вважається коректним, хоча кожен окремий випадок застосування може бути або обґрунтованим або ні. Вивід логіки висловлювань із використанням modus ponens є дедуктивним. Правило виведення (Перенаправлено з Правило виводу)
У логіці правило виведення, правило виводу або правило перетворення — це логічна форма[en], що складається з функції, яка отримує передумови, аналізує їхній синтаксис[en] і повертає висновок (або висновки[en]). Наприклад, правило виведення, що називається modus ponens, отримує дві передумови, одну у формі «Якщо p тоді q», а другу у формі «p», і повертає висновок «q». Це правило є чинним відносно семантики класичної логіки (як і відносно семантик багатьох інших некласичних логік), у тому сенсі що якщо передумови є істинними (в межах інтерпретації), то істинним є і висновок.
Зазвичай правило виведення зберігає істинність, семантичну властивість. У багатозначній логіці воно зберігає узагальнене значення. Але дія правила виведення є винятково синтаксичною, і не потребує зберігання ніякої семантичної властивості: будь-яка функція з множин формул до формул вважається правилом виведення. Зазвичай важливими є лише рекурсивні правила, тобто такі, що існує ефективна процедура[en] визначення, чи є будь-яка задана формула висновком заданої множини формул відповідно до цього правила. Прикладом правила, що не є ефективним у цьому сенсі, є нескінченномісне ω-правило[en].[1] Популярні правила виведення у логіці висловлювань включають modus ponens, modus tollens та контрапозицію. Предикатна логіка першого порядку використовує правила виведення для обходження з логічними кванторами. Зміст
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-24; просмотров: 409; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.124.40 (0.009 с.) |
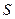 може складатись з переліку аксіом та правил виведення. Нехай
може складатись з переліку аксіом та правил виведення. Нехай  - множина формул, а
- множина формул, а 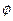 - одна формула формальної мови. Твердження
- одна формула формальної мови. Твердження 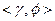 формальною мовою дедуктивно правильне, якщо існує послідовність формул в формальній мові, що завершується
формальною мовою дедуктивно правильне, якщо існує послідовність формул в формальній мові, що завершується 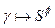 , або просто
, або просто 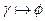 .
.
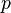
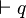
 означає логічний вивід.Аргумент має два вихідних твердження. Перше це умова «якщо-то» або «умовне» твердження, а саме що із P слідує Q. Друге твердження це те що P, умовна частина першого твердження, є істиною. Із цих двох умов логічно слідує що Q, висновок першого твердження, мусить бути істиною також.
означає логічний вивід.Аргумент має два вихідних твердження. Перше це умова «якщо-то» або «умовне» твердження, а саме що із P слідує Q. Друге твердження це те що P, умовна частина першого твердження, є істиною. Із цих двох умов логічно слідує що Q, висновок першого твердження, мусить бути істиною також.


