Приклад нечіткого управління

 

Контролери нечіткої логіки – найбільш важлива область застосування теорії нечітких множин. Їх функціонування відрізняється від роботи звичайних контролерів: для опису роботи використовуються знання експертів замість диференційних рівнянь. Ці знання мають вигляд лінгвістичних змінних, які описуються нечіткими множинами. Розглянемо ці поняття на прикладі "Перевернутого маятника".

Щоглу (рис.11.15), яка закріплена нерухомо у нижньому кінці на візку, потрібно підтримувати вертикальною за рахунок регулювання вихідної змінної - руху візка ліворуч або праворуч зі швидкістю V =-5…+5 м/сек в залежності від вхідних змінних: кутавідхиленнящогли ±α= -45…+45⁰ та кутової швидкості відхиленнящогли ω=dα/dt= -15… +15 (⁰/сек.) (тут знак "-" відноситься до руху ліворуч, а знак "+" - до руху праворуч).

 

 

 

Для початку ми повинні суб’єктивно визначити такі лінгвістичні змінні для універсума швидкості переміщення V=-5…+5 м/сек. (рис. 11.16):

§ ±В (+V=+1…+∞ м/ сек.; -V= -1…-∞ м/ сек. – штрих-пунктирна лінія) - позитивна/негативна велика швидкість;

§ ±М (+V=0…+2 м/сек.; -V=0…-2 м/сек. – безперервна товста лінія) - позитивна/негативна мала швидкість;

§ О (V=-1…+1 м/сек. – штрихова лінія) - нульова швидкість.

 

 

 

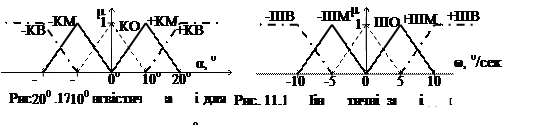
Аналогічні лінгвістичні змінні визначаються для вхідних універсумів:

а) кута між вертикальною віссю та щоглою маятника α =-45…+45⁰ (рис. 11.17):

§ ±КВ (+α=+10…+45⁰; - α= -10…-45 ⁰ – штрих-пунктирна лінія) - позитивний/негативний великий кут;

§ ±КМ (+α=0…+20⁰; - α= -20…0 ⁰ – безперервна товста лінія) - позитивний/негативний малий кут;

§ КО (+α=-10…+10 ⁰ – штрихова лінія) - нульовий кут;

 

 

б) кутова швидкість переміщення щогли маятника ω =dα/dt=-15…+15 (⁰/сек.) (рис. 11.18):

§ ± ШВ (+ω =+5…+45 ⁰/сек.; - ω = -5…-45 ⁰/сек. – штрих-пунктирна лінія) - позитивна/негативна велика швидкість;

§ ±ШМ (+ω =0…+10 ⁰/сек.; - ω = -10…0 ⁰/сек – безперервна товста лінія) - позитивна/негативна мала швидкість;

§ КО (+α= -5…+5 ⁰/сек. – штрихова лінія) - нульовий кут.

Розглянемо, як приклад, чим керується експерт при визначенні правил, які у даному випадку потрібно використовувати для керування рухом візка.

1. Припустимо, що щогла знаходиться близько до центру (кут щогли КО, α =0⁰), кутова швидкість щогли дорівнює нулю (кутова швидкість ШО, ω=0). Це – мета роботи схеми і тому нічого не потрібно змінювати. Тому візок не рухається (лінгвістична швидкість руху візка О, V = 0 м/сек.). В результаті отримуємо правило:

ЯКЩО "α =КО" І " ω=ШО", ТОДІ V =О.

2. Введемо в попередні умови зміну: щогла рухається праворуч (позитивний напрямок) з низькою кутовою швидкістю +ШМ. Природно, що при цьому, щоб збалансувати вертикальне положення щогли, треба переміщувати возик у тому ж напрямі з малою швидкістю +М. В результаті отримуємо правило:

ЯКЩО "α =КО" І " ω=+ШМ", ТОДІ V=+М.

Зведемо усі отримані експертом правила у табл. 11.4. Як бачимо, правила не охоплюють усі їх можливі комбінації.

Таблиця 11.4. Правила визначення експертом швидкості руху візка V в залежності від кута α та кутової швидкості ω.

Кутова швидкість ω	Кут α:
-КВ	-КМ	КО	+КМ	+КВ
-ШВ			-В
-ШМ			-М	О
ШО	-В	-М	О	+М	+В
+ШМ		О	+М
+ШВ			+В

Тепер перейдемо до користування правилами табл. 11.4 при умові, що нам задані вхідні дійсні числові значення кута α та кутової швидкості ω щогли (вони помічені на рис. 11.19 та рис. 11.20. пунктирними лініями). Метою розрахунків є отримання виходу – напрямку та швидкості переміщення візка V. Отримані чотири точки пересічення реальних даних з функціями належності відповідних лінгвістичних змінних КО, +КМ та ШО, -ШМ допускають існування чотирьох правил: для пар КО / ШО, КО / -ШМ, +КМ / ШО, +КМ / -ШМ. Для визначення швидкості візка (–В, -М, О, +М, +В) використовуються для усіх вказаних пар наведені в табл.11.4 лінгвістичні правила визначення швидкості руху візка V в залежності від кута α та кутової швидкості ω.

 

 

1. Для пари КО / ШО використаємо з табл. 11.4 правило " ЯКЩО " α =КО" І " ω=ШО", ТОДІ V=О ". Із рис. 11.19 випливає, що реальне значення кута α належить нечіткій множині КО зі степеню 0,75, а із рис. 11.20 випливає, що реальне значення кутової швидкості ω належить нечіткій множині ШО зі степеню 0,4. Дві частки умови правила об’єднуються логічною умовою " І "; тому з виразу min (0,75; 0,4) отримуємо мінімальний рівень 0,4 для вихідної лінгвістичної змінної "швидкість візка" О (рис. 11.21).

 

Ми виявили вплив на поведінку візка лише одного правила - для пари КО / ШО. Далі ми повинні найти рішення для усіх правил (усіх пар) іоб’єднати їх в одне рішення для визначення швидкості переміщення візка.

2. Для пари КО / -ШМ діє правило " ЯКЩО ((α =КО) І (ω=-ШМ)), ТОДІ (V=-M) ". Із рис. 11.19 та рис. 11.20 визначаємо: реальний кут α відноситься до лінгвістичної змінної КО зі степеню 0,75; кутова швидкість ω відноситься до лінгвістичної змінної -ШМ зі степеню 0,6. З виразу min (0,75; 0,6) отримуємо нечітку множину -М для змінної "швидкість візка" з найменшим рівнем 0,6 (рис. 11.22).

 

 

3. Для пари +КМ / ШО діє правило " ЯКЩО ((α =+КМ) І (ω=ШО)), ТОДІ (V=+М) ". Із рис. 11.19 та рис. 11.20 визначаємо: кут α відноситься до лінгвістичної змінної +КМ зі степеню 0,25; кутова швидкість ω відноситься до лінгвістичної змінної ШО зі степеню 0,4. З виразу min (0,25; 0,4) отримуємо нечітку множину +М для змінної "швидкість візка" з найменшим рівнем 0,25 (рис. 11.23).

	Рис. 11.23. Результат використання правила " ЯКЩО ((α =+КМ) І (ω=ШО)), ТОДІ (V=+М) ".

 

 

4. Для пари +КМ / -ШМ діє правило " ЯКЩО ((α =+КМ) І (ω=-ШМ)), ТОДІ (V=О) ". Із рис. 11.13 та рис. 11.14 визначаємо: кут α відноситься до лінгвістичної змінної +КМ зі степеню 0,25; кутова швидкість ω відноситься до лінгвістичної змінної -ШМ зі степеню 0,6. З виразу min (0,25; 0,6) отримуємо нечітку множину О для змінної "швидкість візка" з найменшим рівнем 0,25 (рис. 11.24).

 

 

 

 

Таким чином, можна указати на такі особливості використання будь-якого правила IF-THEN:

- кожне із правил в частині THEN визначає своє лінгвістичне значення терму виходу з властивою цьому термові логічною функцією належності;

- логічна ступень істинності функції належності терму виходу визначається мінімумом логічної ступені істинності серед усіх термів вхідних даних лівої частини правила IF;

- логічні ступені істинності серед термів вхідних даних лівої частини правила IF визначаються по числових вхідних даних з використанням відповідних функцій належності вхідних термів.

Об’єднання результатів чотирьох правил дає загальне рішення V₁ у вигляді рис. 11.19. При накладанні двох рішень по режиму О (рис.11.21 та рис. 11.24) обирається рішення рис.11.21 з більшим рівнем 0,4.

 

 

Ми отримали для контролера нечітку множину для швидкості. Далі потрібно обрати одне значення для представлення кінцевого вихідного значення, тобто потрібно виконати дефаззіфікацію. Існує кілька евристичних методів дефазіфікації, один з яких, наприклад, пропонує обрати в якості кінцевого значення центр тяжіння нечіткої множини (рис. 11.25).

Така процедура отримання рішення зветься контролером Мамдані (Mamdani controller). Процес навчання контролера полягає у коригуванні функцій належності для отримання вірного виходу V₁ по введеним числовим значенням вхідних змінних α та ω.