
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Работа с окнами системы matlab.Содержание книги Поиск на нашем сайте
Порядок выполнения. 1. Упражнения выполняются параллельно с изучением теоретического материала из параллельного курса «Линейная алгебра и аналитическая геометрия», см. приложения, лекции и другую литературу. 2. Большинство упражнений необходимо предварительно решать в тетради. 3. При выполнении упражнений в случае появления сообщения об ошибке рекомендуется сначала самостоятельно выяснить, чем оно вызвано, и исправить команду; если многократные попытки устранить ошибку не привели к успеху, - проконсультироваться с преподавателем. 4. Дома доделать примеры и упражнения, которые Вы не успели выполнить во время занятия; выполнить дополнительные упражнения для самостоятельной работы и ответить на контрольные вопросы. 5. Подготовить отчёт, в который включить результаты по упражнениям и развернутые ответы на контрольные вопросы. Отчёт представить · № упражнения; текст упражнения; · команды, скопированные из командного окна, с комментариями к ним · результаты их выполнения, включая построенные графики; · выводы и комментарии к полученным результатам. *Без предъявления письменных решений электронный отчет не рассматривается. **При проверке решений и отчета у преподавателя не должно возникать необходимости обращаться к источнику задания. Работа с системой MATLAB. Работа с окнами системы MATLAB. MATLAB (MATrix LABoratory) - интерактивный матрично- ориентированный пакет, предназначенный для выполнения научных и инженерных расчетов. После запуска пакета появляется рабочий стол (Desktop), состоящий из строки заголовка, строки главного меню, панели инструментов и комбинированного окна. Горячие клавиши переключения между окнами Ctrl+F6 или на панели задач нажатием правой кнопкой мыши выберете удобный для вас режим работы с окнами, например, режим «окна сверху вниз», тогда вы будете видеть сразу оба документа. Комбинированное окно (Desktop) включает четыре панели: Command Window (Окно команд) - самое используемое окно. В нем набирают команды пользователя, подлежащие немедленному исполнению. Здесь же выдаются результаты выполненных команд.
Command History (История команд) хранит все команды, набираемые пользователем, однако в отличие от содержимого Command Window (Окно команд) сюда не попадают сообщения системы и результаты вычислений.
Workspace (Рабочее пространство) отображает текущий набор переменных, заведенных пользователем в командном окне. Current Directory (Текущий каталог) является аналогом известной программы Проводник, но имеет для MATLAB свое особое предназначение. Дело в том, что, кроме работы с математическими выражениями из командного окна, пользователь также может работать с файлами.
Переключение между окнами MATLAB реализуется с помощью щелчка левой кнопки мыши в области соответствующего окна или на одной из вкладок, если нужное окно полностью закрыто другим окном. Конфигурацию окон на экране можно менять, используя вертикальные и горизонтальные разделители. Можно изменять размер окон в пределах рабочего стола, перемещать окна по экрану с помощью перетаскивания строки заголовка соответствующего окна, закрывать их (крестик) и отделять от рабочего стола (стрелочка). Чтобы в точности восстановить исходную конфигурацию нужно пройти путь: Desktop (команда Рабочий стол в строке главного меню) → Desktop Layout (разметка рабочего стола) → Default (по умолчанию). Для сохранения собственной конфигурации выберите Save Layout. Упражнение 1. Работа с окнами системы MATLAB. 1. Последовательно переключитесь между окнами Command Window, Command History, Current Directory, Workspace, Command Window. 2. С помощью вертикального разделителя уменьшите вдвое ширину Command Window, увеличив при этом ширину окон Workspace и Command History. 3. Отсоедините окно Current Directory с помощью стрелочки Undock Current Directory в правом верхнем углу окна Current Directory слева от крестика Close Current Directory и перенесите его в правый нижний угол рабочего стола МАТЛАБ, после чего сверните его. 4. Присоедините к рабочему столу Current Directory, нажав на стрелочку Dock Current Directory в правом верхнем углу окна Current Directory 5. Удалить с рабочего стола Current Directory, нажав на крестик Close Current Directory в правом верхнем углу этого окна. 6. Перетащите Command History в левый верхний угол рабочего стола, с помощью перетаскивания за строку с названием окна, дождитесь пока в левом верхнем углу появиться контур нового положения окна. В результате выполнения команд окно Current Directory должно оказаться под окном Workspace. 7. Удалите с рабочего стола Command History. Вернуть его, с помощью последовательности команд: Desktop ( команда Рабочий стол в строке главного меню ) → Workspace (поставить галочку). 8. С помощью горизонтального разделителя увеличить примерно на треть высоту Workspace. 9. Удалить с рабочего стола Workspace, с помощью последовательности команд: Desktop( команда Рабочий стол в строке главного меню ) → Workspace ( убрать галочку ). Вернуть его, с помощью последовательности команд: Desktop → Workspace (поставить галочку). 10. Восстановить исходную конфигурацию рабочего стола: Desktop → Desktop Layout → Default (по умолчанию). 11. Выберете для себя наиболее удобную конфигурацию расположения окон и сохраните ее: Desktop → Save Layout Command Window. Как уже говорилось выше Command Window – командное окно -самое используемое окно. Знак «>>» символизирует начало текущей строки. В этой строке можно набирать формулы или команды, удовлетворяющие синтаксису языка MATLAB. Если все составляющие (операнды) формулы известны, то после нажатия клавиши «Enter» MATLAB вычисляет значение выражения. Если в выражении указан операнд, значение которого неизвестно, MATLAB выдает сообщение об ошибке. В таблице 1 представлены основные горячие клавиши:
Строка главного меню. Меню Edit (Правка) содержит команды по вырезанию (Cut - вырезать), копированию (Copy - копировать), вставке (Paste - вставить), удалению (Delete - удалить) выделенных фрагментов текстов или графических объектов. Команда Select All (выделить все) выделяет весь текст командного окна, который можно копировать. Еще одна группа команд позволяет очистить соответствующие окна (Clear Command Window - очистить окно команд, Clear Command History - очистить окно истории команд, Clear Workspace - очистить переменные рабочего пространства). Строка главного меню работает для активного окна. Переключая окна, мы делаем какое-то из них активными. Вычисления в МАТЛАБ. Все операции в MATLAB реализуются посредством функций. Например, для выполнения операции сложения MATLAB вызывает стандартную функцию plus(), для выполнения операции вычитания - функцию minus(). При этом команды для вычисления выражений имеют вид, свойственный всем языкам программирования высокого уровня: «+», «−», «*», «/», «^», «sqrt», «nthroot», см. в help MATLAB раздел Arithmetic Operators, а также. Л.1 стр. 27.
Примеры. Вычислений в МАТЛАБ. Операция сложение. Наберите в командной строке 1+2 и нажмите <Enter>. В результате в командном окне МАТЛАБ отображается следующее: >> 1+2 ans = >> Что сделала программа МАТЛАБ? Сначала она вычислила сумму 1+2, затем записала результат в специальную переменную ans и вывела ее значение, равное 3, в командное окно. Ниже ответа расположена командная строка с мигающим курсором, обозначающая, что МАТЛАБ готова к дальнейшим вычислениям. Можно набирать в командной строке новые выражения и находить их значения. Если требуется продолжить работу с предыдущим выражением, например, вычислить (1+2)/4.5, то проще всего воспользоваться уже имеющимся результатом, который хранится в переменной ans. Наберите в командной строке ans/4.5 (при вводе десятичных дробей используется точка) и нажмите <Enter>, получается: >> ans/4.5 ans = 0.6667
В именах переменных можно использовать латинские буквы, цифры и символ подчеркивания; большие и малые буквы в именах различаются; имя должно начинаться с буквы; длина имени не должна превышать 63 символа. >> s=1+2 s = >> d= s/4.5 d = 0.6667 Замечание. Есть целый ряд системных числовых констант, которые нельзя портить, то есть использовать для обозначения переменных: pi - число realmax - наибольшее положительное число с плавающей запятой; realmin - наименьшее положительное число с плавающей запятой; eps - относительная погрешность при вычислениях с плавающей запятой Пример. Точка с запятой. Введите. >> a=5, b=3; c=6; h1=(a+b)*c; h2=a-b+c a = 5 h2 = 8 Мы не подавили вывод переменных а и h2. Для того чтобы узнать чему все же равна переменная h1, вызовем ее: >> h1 h1 = 48 Пример. Переменные рабочего пространства. >> whos a b h1 h2 Name Size Bytes Class Attributes
a 1x1 8 double b 1x1 8 double h1 1x1 8 double h2 1x1 8 double
Name - имя переменой, Size - размерность, Bytes - количество занятых байтов, Class - класс объектов, представляющих соответствующий тип данных. Команда whos без параметров выдает информацию обо всех переменных. Если в дальнейших вычислениях переменная a, к примеру, не понадобится, ее можно убрать из рабочего пространства, набрав в командном окне clear a. Команда clear без параметров удаляет все переменные.
Пример. Работа с алгебраическими выражениями, с символьными переменными. Введите >> clear all >> f=(x+1)*(x-1) ??? Undefined function or variable 'x'. МАТЛАБ выдал сообщение об ошибке. Теперь введите >> syms x >> f=(x+1)*(x-1) f = (x - 1)*(x + 1) МАТЛАБ вывел алгебраическое выражение. Посмотрите в help команды-simplifications (упрощения): как делать различные преобразования в алгебраических выражениях. Введите >> f=collect(f) f = x^2 - 1 Ответьте в отчете на вопрос, что сделала команда «collect» с выражением f? Пример. Работа с алгебраическими выражениями. Подстановка чисел. Теперь присвоим x какое-нибудь число: >>x = 2 снова вызовем f >> f f = (x+1)*(x-1) ничего не изменилось, но если набрать заново алгебраическое выражение f=(x+1)*(x-1) (можно просто выбрать данную команду при помощи стрелок) >> f=(x+1)*(x-1) f = 3 Мы получим значение функции f=3, при x = 2.
Пример. Упрощение алгебраических выражений. При помощи различных команд simplifications (упрощения) записать различные формулы сокращенного умножения: разность квадратов; квадрат суммы, разности; куб суммы, разности; разность кубов, сумма кубов. В качестве символьных переменных можно выбрать не только буквы, но и числа. Например, если нужно раскрыть скобки в выражении >> (sqrt(2)+sqrt(6))^2 ans = 14.9282 вычисляет значение выражения Теперь введем >> a=sym(sqrt(6)) a = 6^(1/2) >> b=sym(sqrt(2)) b = 2^(1/2) >> (a+b)^2 ans = (2^(1/2) + 6^(1/2))^2
>> w=simple(ans) w = 4*3^(1/2) + 8 Теперь мы раскрыли скобки и привели подобные слагаемые и получили ответ в радикалах: А для того чтобы узнать его примерное значение введем >> 4*3^(1/2) + 8 ans = 14.9282
Посмотрите через help функцию sym. Команда sym позволяет вводить ограничения на свойства переменных: Решим уравнение: >> clear all solve('x^4-1=0') ans = -1 -i i
Уравнение имеет действительные и комплексные корни. Теперь введем ограничение на переменную: x – вещественное (действительное) число. >> x = sym('x', 'real') x = x >> solve('x^4-1=0') ans = -1 Выведены только вещественные значения корней уравнения.
Массивы в MATLAB. Примеры. Задание матриц. 1. Для задания вектора - строки (т.е. матрицы размера >> str1 = [3 4 9 2] str1 = 3 4 9 2 >> str2 = [5, 3, 3, 2] str2 = 5 3 3 2 >> 2. Для задания вектор- столбца (т.е. матрицы размера >> st = [1.2; 5.3; 6.4] a = 1.2000 5.3000 6.4000 >> 3. Комбинируя оба варианта разделителя, можно задать матрицу, число строк и столбцов которой больше одного (двумерный массив): >> A=[1 2 3 4;0 -1 -3 -2] A = 1 2 3 4 0 -1 -3 -2 4. Любое число рассматривается в MATLAB как матрица размера >> n=3 n = 3 >> m=[3] m = 3 5. Снова просмотрите каждую переменную в окне Workspace. >> whos str1 str2 st A n m Name Size Bytes Class Attributes A 2x4 64 double m 1x1 8 double n 1x1 8 double st 3x1 24 double str1 1x4 32 double str2 1x4 32 double 6. Узнайте n-мерность (измерение) и размерность переменных str1, str2, st, A, n, m, при помощи встроенных функций ndims и size, сделайте выводы: >> ndims(A) ans = >> size(A) ans = 2 4 Матрица A хранится в двумерном (ndims(A)) массиве размерностью (size(A)) 3х1 (три на один): вектор-столбец A состоит из трех строк и одного столбца. Упражнение 3. Проделайте аналогичные операции для остальных переменных str1, str2, st, n, m,. Сделайте выводы.
Итак, важно понять, что число, вектор-строка, вектор-столбец или матрица являются математическими объектами, которые представляются двумерными массивами. N-мерные массивы данных Приведем примеры массивов другой размерности. Примеры. N-мерные массивы Команда rand(k,l,n,m) позволяет создавать матрицу с произвольными числами (от 0 до 1) размерности k x l (k строк, l столбцов), n, m - добавляют единицы измерения, например >> E1=rand(1,4) %создаем матрицу размерности 1x4 E1 = 0.7922 0.9595 0.6557 0.0357 >> ndims(E1) % увидим, что E1 - двумерный массив ans = >> E2=rand(size(st)) %создаем матрицу той же размерности, что и st, 3x1 E2 = 0.9340 0.6787 0.7577 >> ndims(E2) % убедимся: E2 - двумерный массив ans = 2 Заметим следующее: >> n1=size(E1) n1 = 1 4 >> size(n1) % это тоже, что и size(size(E1)) ans = 1 2 >> length(n1) ans = 2 >> length(size(E1)) ans = >> ndims(E1) ans = length() – возвращает наибольшее из чисел размерности-size массива То есть ndims(E1)=length(size(E1))
Проверьте этот факт для остальных переменных рабочего пространства. >> E3=rand(3,2,2) % создадим трехмерный массив E3(:,:,1) = 0.0046 0.8687 0.7749 0.0844 0.8173 0.3998 E3(:,:,2) = 0.2599 0.9106 0.8001 0.1818 0.4314 0.2638 Образно говоря, мы получили «многоэтажный дом». Теперь, чтобы обратиться к элементам трехмерного массива, нужно задать номера строки, столбца и «этажа». В данном массиве два этажа, «в каждом этаже» по три строки и по два столбца. >> ndims(E3) ans = 3 E3(:,:,1) – выводит первую матрицу 3х2, E3(:,:,2) –выводит вторую матрицу 3х2 Роль символа двоеточия «:» интуитивно понятен, позже будет объяснение и плотная работа с этим символом. >> E4=rand(1,2,3,2) %создадим четырехмерный массив E4(:,:,1,1) = 0.3692 0.1112 E4(:,:,2,1) = 0.7803 0.3897 E4(:,:,3,1) = 0.2417 0.4039 E4(:,:,1,2) = 0.0965 0.1320 E4(:,:,2,2) = 0.9421 0.9561 E4(:,:,3,2) = 0.5752 0.0598 Мы получили «улицу» из «одинаково этажных домов». Теперь, чтобы обратиться к элементам четырехмерного массива, нужно задать номера строки, столбца, «этажа» и «номер дома». В данном массиве два дома, по три этажа в каждом, на каждом «этаже» одна строка и три столбца. E4(:,:,3,1) - выводит третий массив первого уровня, E4(:,:,2,2) – выводит второй массив второго уровня. >> ndims(E4) ans = 4 И мы снова видим: ndims(A)=length(size(A)) >> n3=size(E3) n3 = 3 2 2 >> length(n3) ans = >> n4=size(E4) n4 = 3 2 2 2 >> length(n4) ans = 4
Итак, все данные в MATLAB представляются в виде массивов. Очень важно правильно понять, как устроены массивы. Без этого невозможна эффективная работа в MATLAB, в частности построение графиков, решение задач линейной алгебры, обработки данных, статистики и многих других. Массив - упорядоченная, пронумерованная совокупность однородных данных. У массива должно быть имя. Массивы различаются по числу размерностей или измерений. Доступ к элементам осуществляется при помощи индекса. Еще раз: число, вектор-строка, вектор-столбец или матрица являются математическими объектами, массивы - способы хранения этих объектов в компьютере. Всюду дальше чаще будут использоваться слова «вектор» и «матрица», так как для нас больший интерес представляет сам объект, чем способ его хранения. Слово «массив» будет использоваться и для вектора, и для матрицы, когда их различие будет несущественным.
3. Различные способы задания массивов. Матрицы Матрица - математический объект, записываемый в виде прямоугольной таблицы чисел, которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы. Если у матрицы количество строк m совпадает с количеством столбцов n, то такая матрица называется квадратной, а число m = n называется размером квадратной матрицы или её порядком.
Примеры. Задание матрицы в MATLAB: Основной способ: с помощью оператора квадратные скобки: [ ] >> A = [1 3; 2 4] A = 1 3 2 4 >> B = [1:3;4:6;7:9] B = 1 2 3 4 5 6 7 8 9 >> C = [B(1:2,:); A(1:3)] C = 1 2 3 4 5 6 1 2 3 Особые матрицы: Матрица из единиц: ones(…) Матрица из нулей: zeros(…) Единичная матрица: eye(…) – на главной диагонали стоят единицы, на остальных местах нули.
>> eye(2,2) ans = 1 0 0 1 >> eye(2,3) ans = 1 0 0 0 1 0 >> eye(3,2) ans = 1 0 0 1 0 0 >> eye(3) ans = 1 0 0 0 1 0 0 0 1
Векторы Матрица из одной строки называется вектор-строкой, из одного столбца – вектор-столбцом, такие матрицы мы будем называть просто векторами.
Упражнение 4.. Различные способы задания векторов. 1) Задать вектор-строку a) ввода чисел c пробелами; b) ввода чисел с запятыми; c) стандартной функцией horzcat(,,,) d) двоеточия «:» с шагом можно задать те же числа от 1 до 6 с шагом 1 2)Задать вектор- столбец a) точки запятой «;»; b) транспонировав вектор-строку, с помощью символа «'» -одинарная кавычка (буква э в латинском регистре) с) стандартной функцией vertcat(,,,) d) двоеточия «:» с шагом и транспонирования «'». Сцепление векторов. 1. Из нескольких вектор-столбцов можно составить один, используя квадратные скобки и разделяя исходные вектор-столбцы точкой с запятой: >> v1 = [1; 2]; v2 = [3; 4; 5]; v = [v1; v2] v = >> 2. Для сцепления вектор-строк также применяются квадратные скобки, но сцепляемые вектор-строки отделяются пробелами или запятыми: >> w1 = [1 2]; w2 = [3 4 5]; w = [w1 w2] w = 1 2 3 4 5
Операции над векторами Упражнение 5. 1. Вычислите сумму массивов a = [1.2; 5.3; 6.4]; b = [7.83; 8.72; 9.61]; 2. Найдите разность b и a, результат запишите в c2 и выведите его в командное окно. Поэлементное умножение (операция «.*») и поэлементное возведение в степень (операция «.^»). 1. Операторам «*» и «.*» соответствуют встроенные в MATLAB в ядро функции mtimes() и times(). Первая функция выполняет матричное умножение входных параметров, а вторая их поэлементное умножение. При умножении вектора на скаляр обе функции вернут одинаковый результат. К матричному умножению мы обратимся в последующих модулях. Операция «.*» (не вставляйте пробел между точкой и звездочкой!) приводит к поэлементному умножению векторов одинаковой длины. В результате получается вектор с элементами, равными произведению соответствующих элементов исходных векторов: Введем две вектор–строки и перемножим их: >> u1=[2 -3 4 1]; u2 = [7 5 -6 9];u=u1.*u2 u = 14 -15 -24 9 Проверьте, использование оператора «*» приведет к сообщению об ошибке. 2. При помощи «.^» осуществляется поэлементное возведение в степень: >> p=u1.^2 p = 4 9 16 1 Проверьте, использование оператора «^» приведет к сообщению об ошибке.
Операции над матрицами Умножение матрицы на число. Умножение матрицы A на число λ заключается в построении матрицы B, элементы которой получены путём умножения каждого элемента матрицы A на это число λ. Сложение матриц Сложение матриц A и B есть операция нахождения матрицы C, все элементы которой равны попарной сумме всех соответствующих элементов матриц A и B. Комплексное сопряжение Если элементами матрицы являются комплексные числа, то комплексно сопряжённая матрица состоит из комплексно сопряженных чисел. Транспонирование матрицы При транспонировании матрицы строки становятся столбцами. Эрмитово сопряжение – комплексное сопряжение и транспонирование: Для матрицы, заданной действительными числами, не комплексными!, операция сопряжения и транспонирования совпадают)
>> A=[2,1] A = 2 1 >> A.' ans = >> A' ans = >> A=[1-i*2,1] A = 1.0000 - 2.0000i 1.0000 >> A' % 'эрмитово сопряжение, превратит строку в столбец и "сопряжет" комплексное число ans = 1.0000 + 2.0000i 1.0000 >> B=[1-i*2 1-i*3;1+i*4,1+i*5;2,3] B = 1.0000 - 2.0000i 1.0000 - 3.0000i 1.0000 + 4.0000i 1.0000 + 5.0000i 2.0000 3.0000 >> B.' ans = 1.0000 - 2.0000i 1.0000 + 4.0000i 2.0000 1.0000 - 3.0000i 1.0000 + 5.0000i 3.0000 >> B' ans = 1.0000 + 2.0000i 1.0000 - 4.0000i 2.0000 1.0000 + 3.0000i 1.0000 - 5.0000i 3.0000 Умножение матриц Умножение матриц A и B – есть операция вычисления матрицы C=AB, элементы которой равны сумме произведений элементов в соответствующей строке первого множителя и столбце второго. Количество столбцов в матрице A должно совпадать с количеством строк в матрице B. Если матрица A имеет размерность m x n, матрица B имеет размерность n x p, то размерность их произведения, матрицы C=AB, будет m x p. Операция матричного умножения «*» двух матриц выполнима только в том случае, если число столбцов в первом сомножителе равно числу строк во втором; в этом случае говорят, что форма матриц согласована. В частности, умножение всегда выполнимо, если оба сомножителя - квадратные матрицы одного и того же порядка. Следует заметить, что из существования произведения AB вовсе не следует существование произведения BA.
Упражнение 6. Выполнить в тетради + MATLAB. Для матриц A' % эрмитово сопряжение A.' % транспонирование B' % эрмитово сопряжение B.' % транспонирование % умножение на число: A1 = 2*A, A2=A*3, A3=4.*A, A4=A*.5 % сложение матриц: C1 = A+B, C2=A+D2, C3=B+D1, C4=A+E2, C5=B+C1 %умножение матриц: % что меняет умножение квадратной матрицы на единичную E? F1 = A*B, F2=B*A, F3=B' *A'б F4=E2*B, F5=A*E1, F=F1*F1*F1 F6=F1*E3, F7=E3*F1 % поэлементное умножение матриц: C = A.*D2 % возведение матрицы А в степень, (то же что и B=A*A, выполнимо только для квадратных матриц) A^2 % невыполнимо F1^2 % выполнимо A.^2 % возведение каждого элемента матрицы А в степень
Упражнение 7. 1) Проверить на примерах 10 свойств операций над матрицами 2) Ввести матрицы
2) Выполнить операции (или убедиться, что их выполнить нельзя):
Примеры. 1. Доступ к элементам вектор–столбца или вектор–строки осуществляется при помощи индекса, заключаемого в круглые скобки после имени массива, в котором хранится вектор. Если среди переменных рабочей среды есть массив v, определенный вектор–строкой >> v = [1.3 3.6 7.4 8.2 0.9]; то для вывода, например его четвертого элемента, используется индексация: >> v(4) ans = 8.2000 2. Появление элемента массива в левой части оператора присваивания приводит к изменению в массиве >> v(2)=-55 v = 1.3000 -55.0000 7.4000 8.2000 0.9000 3. Из элементов массива можно формировать новые массивы, например >> u = [v(3); v(2); v(1)] u = 7.4000 -55.0000 1.3000 4. Для помещения определенных элементов одного вектора в другой вектор в заданном порядке служит индексация при помощи вектора. Запись в массив w четвертого, второго и пятого элементов v производится следующим образом: >> w=v([4,2,5]) w = 8.2000 -55.0000 0.9000 >> w=v([3,1,3,1,1]) w = 7.4000 1.3000 7.4000 1.3000 1.3000 >> v=v' v = 1.3000 -55.0000 7.4000 8.2000 0.9000 >> w=v([3,1,3]) w = 7.4000 1.3000 7.4000 5. MATLAB предоставляет удобный способ обращения к блокам последовательно расположенных элементов вектора. Для этого служит индексация при помощи знака двоеточия. Предположим, что в массиве w, соответствующем вектор–строке из семи элементов, требуется заменить нулями элементы со второго по шестой. Индексация при помощи двоеточия позволяет просто и наглядно решить поставленную задачу: >> w = [0.1 2.9 3.3 5.1 2.6 7.1 9.8]; >> w(2:5) = 0; >> w w = 0.1000 0 0 0 0 7.1000 9.8000 Присваивание w(2:5) = 0 эквивалентно последовательности команд Можем изменять элементы через определенный шаг: >> w(1:2:7) = -1; >> w w = -1.0000 0 -1.0000 0 -1.0000 7.1000 -1.0000
6. Индексация при помощи двоеточия оказывается удобной при выделении части из большого объема данных в новый массив: >> w = [0.1 2.9 3.3 5.1 2.6 7.1 9.8]; >> w1=w(1:2:7) w1 = 0.1000 3.3000 2.6000 9.8000 Упражнение 8. Составьте массив w2, содержащий элементы w кроме четвертого. В этом случае удобно использовать двоеточие и сцепление строк:
8. Элементы массива могут входить в выражения. Нахождение, например среднего геометрического из элементов массива u, можно выполнить следующим образом: >> gm = (u(l)*u(2)*u(3))^(l/3) Данная запись равносильна выражению gm = 17.4779 Число (1/3) необходимо взять в скобки, иначе мы получим выражение Команда >> gm = (u(1)*u(2)*u(3))^1/3 дает совсем другой ответ: gm = 1.7797e+003
Упражнение 9. Создать с помощью специальных символов вектор–строку
Примеры. Для доступа к отдельным элементам матриц указываются их индексы: 1. Например, А(1,3) - элемент матрицы А, стоящий в 1-й строке и 3-м столбце А(2,1) - элемент матрицы А, стоящий во 2-й строке и 1-м столбце >> A A = 1 2 3 4 0 -1 -3 -2 >> A(1,3) ans = >> A(2,1) ans = 0 2. Элементы матрицы A можно вызвать иначе >> A(5) ans = >> A(2) ans =
А(1,3) - пятый элемент матрицы А, А(2,1) - второй элемент матрицы А. МАТЛАБ «считает» элементы матрицы сверху вниз по столбцам:
Список рекомендуемой литературы 1. А. Кривелёв. Основы компьютерной математики с использованием системы MatLab. М, 2005. 2. В.А.Ильин, Э.Г.Позняк. Аналитическая геометрия. М.,Наука,2001, Шифр - 514.12(075.8) И-46. 3. Ржавинская Е.В., Соколова Т.В., Олейник Т.А. Лекции по линейной алгебре и аналитической геометрии, М.,МИЭТ. 2007. 4. Сборник задач по математике для втузов под редакцией А.В.Ефимова, А.С.Поспелова. В 4 частях. Часть 1.(4-е изд. перераб. и доп.)2001, 2004.
Порядок выполнения. 1. Упражнения выполняются параллельно с изучением теоретического материала из параллельного курса «Линейная алгебра и аналитическая геометрия», см. приложения, лекции и другую литературу. 2. Большинство упражнений необходимо предварительно решать в тетради. 3. При выполнении упражнений в случае появления сообщения об ошибке рекомендуется сначала самостоятельно выяснить, чем оно вызвано, и исправить команду; если многократные попытки устранить ошибку не привели к успеху, - проконсультироваться с преподавателем. 4. Дома доделать примеры и упражнения, которые Вы не успели выполнить во время занятия; выполнить дополнительные упражнения для самостоятельной работы и ответить на контрольные вопросы. 5. Подготовить отчёт, в который включить результаты по упражнениям и развернутые ответы на контрольные вопросы. Отчёт представить · № упражнения; текст упражнения; · команды, скопированные из командного окна, с комментариями к ним · результаты их выполнения, включая построенные графики; · выводы и комментарии к полученным результатам. *Без предъявления письменных решений электронный отчет не рассматривается. **При проверке решений и отчета у преподавателя не должно возникать необходимости обращаться к источнику задания. Работа с системой MATLAB. Работа с окнами системы MATLAB. MATLAB (MATrix LABoratory) - интерактивный матрично- ориентированный пакет, предназначенный для выполнения научных и инженерных расчетов. После запуска пакета появляется рабочий стол (Desktop), состоящий из строки заголовка, строки главного меню, панели инструментов и комбинированного окна. Горячие клавиши переключения между окнами Ctrl+F6 или на панели задач нажатием правой кнопкой мыши выберете удобный для вас режим работы с окнами, например, режим «окна сверху вниз», тогда вы будете видеть сразу оба документа. Комбинированное окно (Desktop) включает четыре панели: Command Window (Окно команд) - самое используемое окно. В нем набирают команды пользователя, подлежащие немедленному исполнению. Здесь же выдаются результаты выполненных команд.
Command History (История команд) хранит все команды, набираемые пользователем, однако в отличие от содержимого Command Window (Окно команд) сюда не попадают сообщения системы и результаты вычислений.
Workspace (Рабочее пространство) отображает текущий набор переменных, заведенных пользователем в командном окне. Current Directory (Текущий каталог) является аналогом известной программы Проводник, но имеет для MATLAB свое особое предназначение. Дело в том, что, кроме работы с математическими выражениями из командного окна, пользователь также может работать с файлами.
Переключение между окнами MATLAB реализуется с помощью щелчка левой кнопки мыши в области соответствующего окна или на одной из вкладок, если нужное окно полностью закрыто другим окном. Конфигурацию окон на экране можно менять, используя вертикальные и горизонтальные разделители. Можно изменять размер окон в пределах рабочего стола, перемещать окна по экрану с помощью перетаскивания строки заголовка соответствующего окна, закрывать их (крестик) и отделять от рабочего стола (стрелочка). Чтобы в точности восстановить исходную конфигурацию нужно пройти путь: Desktop (команда Рабочий стол в строке главного меню) → Desktop Layout (разметка рабочего стола) → Default (по умолчанию). Для сохранения собственной конфигурации выберите Save Layout.
|
|||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 4984; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.237.52 (0.013 с.) |

 ;
;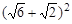 , то ввод
, то ввод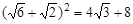 .
.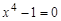 .
. ) используются квадратные скобки, в которых числовые данные отделяются друг от друга пробелами или запятыми:
) используются квадратные скобки, в которых числовые данные отделяются друг от друга пробелами или запятыми: ) используются квадратные скобки, в которых числовые данные отделяются друг от друга точкой с запятой:
) используются квадратные скобки, в которых числовые данные отделяются друг от друга точкой с запятой: .
. с помощью
с помощью с помощью
с помощью и
и  , запишите результат в массив с1, и выведите все векторы в командное окно.
, запишите результат в массив с1, и выведите все векторы в командное окно. ,
,  , c=2, D1=ones(2,3), D2=ones(3,2),E1=eye(2,3), E2=eye(3,2), E3=eye(3), (ввести символьно соответствующие элементы: syms a11 a12 итд.), осуществить операции:
, c=2, D1=ones(2,3), D2=ones(3,2),E1=eye(2,3), E2=eye(3,2), E3=eye(3), (ввести символьно соответствующие элементы: syms a11 a12 итд.), осуществить операции: ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
. ,
, 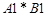 ,
,  ,
,  ,
,  ,
, 
 ,
,  ,
,  ,
, 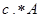 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 
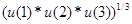
 ,
, и вектор–столбец
и вектор–столбец  . Изменить значение второй координаты вектора
. Изменить значение второй координаты вектора  на -5, значение третьей координаты вектора
на -5, значение третьей координаты вектора 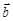 - на сумму первой и второй координаты вектора
- на сумму первой и второй координаты вектора 


