
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Матричное представление данныхСодержание книги Поиск на нашем сайте
Матрицей размерности Если матрица имеет размер Если матрица имеет размер В MATLAB все числовые данные представляются в виде матриц. Поэтому любое число тоже рассматривается как матрица размера Рассмотрим способы задания матриц в MATLAB. Примеры. Задание матриц. 1. Для задания вектора - строки (т.е. матрицы размера >> str1 = [3 4 9 2] str1 = 3 4 9 2 >> str2 = [5, 3, 3, 2] str2 = 5 3 3 2 >> 2. Для задания вектор- столбца (т.е. матрицы размера >> st = [1.2; 5.3; 6.4] a = 1.2000 5.3000 6.4000 >> 3. Комбинируя оба варианта разделителя, можно задать матрицу, число строк и столбцов которой больше одного (двумерный массив): >> A=[1 2 3 4;0 -1 -3 -2] A = 1 2 3 4 0 -1 -3 -2 4. Любое число рассматривается в MATLAB как матрица размера >> n=3 n = 3 >> m=[3] m = 3 5. Снова просмотрите каждую переменную в окне Workspace. >> whos str1 str2 st A n m Name Size Bytes Class Attributes A 2x4 64 double m 1x1 8 double n 1x1 8 double st 3x1 24 double str1 1x4 32 double str2 1x4 32 double 6. Узнайте n-мерность (измерение) и размерность переменных str1, str2, st, A, n, m, при помощи встроенных функций ndims и size, сделайте выводы: >> ndims(A) ans = >> size(A) ans = 2 4 Матрица A хранится в двумерном (ndims(A)) массиве размерностью (size(A)) 3х1 (три на один): вектор-столбец A состоит из трех строк и одного столбца. Упражнение 3. Проделайте аналогичные операции для остальных переменных str1, str2, st, n, m,. Сделайте выводы.
Итак, важно понять, что число, вектор-строка, вектор-столбец или матрица являются математическими объектами, которые представляются двумерными массивами. N-мерные массивы данных Приведем примеры массивов другой размерности. Примеры. N-мерные массивы Команда rand(k,l,n,m) позволяет создавать матрицу с произвольными числами (от 0 до 1) размерности k x l (k строк, l столбцов), n, m - добавляют единицы измерения, например
>> E1=rand(1,4) %создаем матрицу размерности 1x4 E1 = 0.7922 0.9595 0.6557 0.0357 >> ndims(E1) % увидим, что E1 - двумерный массив ans = >> E2=rand(size(st)) %создаем матрицу той же размерности, что и st, 3x1 E2 = 0.9340 0.6787 0.7577 >> ndims(E2) % убедимся: E2 - двумерный массив ans = 2 Заметим следующее: >> n1=size(E1) n1 = 1 4 >> size(n1) % это тоже, что и size(size(E1)) ans = 1 2 >> length(n1) ans = 2 >> length(size(E1)) ans = >> ndims(E1) ans = length() – возвращает наибольшее из чисел размерности-size массива То есть ndims(E1)=length(size(E1))
Проверьте этот факт для остальных переменных рабочего пространства. >> E3=rand(3,2,2) % создадим трехмерный массив E3(:,:,1) = 0.0046 0.8687 0.7749 0.0844 0.8173 0.3998 E3(:,:,2) = 0.2599 0.9106 0.8001 0.1818 0.4314 0.2638 Образно говоря, мы получили «многоэтажный дом». Теперь, чтобы обратиться к элементам трехмерного массива, нужно задать номера строки, столбца и «этажа». В данном массиве два этажа, «в каждом этаже» по три строки и по два столбца. >> ndims(E3) ans = 3 E3(:,:,1) – выводит первую матрицу 3х2, E3(:,:,2) –выводит вторую матрицу 3х2 Роль символа двоеточия «:» интуитивно понятен, позже будет объяснение и плотная работа с этим символом. >> E4=rand(1,2,3,2) %создадим четырехмерный массив E4(:,:,1,1) = 0.3692 0.1112 E4(:,:,2,1) = 0.7803 0.3897 E4(:,:,3,1) = 0.2417 0.4039 E4(:,:,1,2) = 0.0965 0.1320 E4(:,:,2,2) = 0.9421 0.9561 E4(:,:,3,2) = 0.5752 0.0598 Мы получили «улицу» из «одинаково этажных домов». Теперь, чтобы обратиться к элементам четырехмерного массива, нужно задать номера строки, столбца, «этажа» и «номер дома». В данном массиве два дома, по три этажа в каждом, на каждом «этаже» одна строка и три столбца. E4(:,:,3,1) - выводит третий массив первого уровня, E4(:,:,2,2) – выводит второй массив второго уровня. >> ndims(E4) ans = 4 И мы снова видим: ndims(A)=length(size(A)) >> n3=size(E3) n3 = 3 2 2 >> length(n3) ans = >> n4=size(E4) n4 = 3 2 2 2 >> length(n4) ans = 4
Итак, все данные в MATLAB представляются в виде массивов. Очень важно правильно понять, как устроены массивы. Без этого невозможна эффективная работа в MATLAB, в частности построение графиков, решение задач линейной алгебры, обработки данных, статистики и многих других.
Массив - упорядоченная, пронумерованная совокупность однородных данных. У массива должно быть имя. Массивы различаются по числу размерностей или измерений. Доступ к элементам осуществляется при помощи индекса. Еще раз: число, вектор-строка, вектор-столбец или матрица являются математическими объектами, массивы - способы хранения этих объектов в компьютере. Всюду дальше чаще будут использоваться слова «вектор» и «матрица», так как для нас больший интерес представляет сам объект, чем способ его хранения. Слово «массив» будет использоваться и для вектора, и для матрицы, когда их различие будет несущественным.
3. Различные способы задания массивов. Матрицы Матрица - математический объект, записываемый в виде прямоугольной таблицы чисел, которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы. Если у матрицы количество строк m совпадает с количеством столбцов n, то такая матрица называется квадратной, а число m = n называется размером квадратной матрицы или её порядком.
Примеры. Задание матрицы в MATLAB: Основной способ: с помощью оператора квадратные скобки: [ ] >> A = [1 3; 2 4] A = 1 3 2 4 >> B = [1:3;4:6;7:9] B = 1 2 3 4 5 6 7 8 9 >> C = [B(1:2,:); A(1:3)] C = 1 2 3 4 5 6 1 2 3 Особые матрицы: Матрица из единиц: ones(…) Матрица из нулей: zeros(…) Единичная матрица: eye(…) – на главной диагонали стоят единицы, на остальных местах нули.
>> eye(2,2) ans = 1 0 0 1 >> eye(2,3) ans = 1 0 0 0 1 0 >> eye(3,2) ans = 1 0 0 1 0 0 >> eye(3) ans = 1 0 0 0 1 0 0 0 1
Векторы Матрица из одной строки называется вектор-строкой, из одного столбца – вектор-столбцом, такие матрицы мы будем называть просто векторами.
Упражнение 4.. Различные способы задания векторов. 1) Задать вектор-строку a) ввода чисел c пробелами; b) ввода чисел с запятыми; c) стандартной функцией horzcat(,,,) d) двоеточия «:» с шагом можно задать те же числа от 1 до 6 с шагом 1 2)Задать вектор- столбец a) точки запятой «;»; b) транспонировав вектор-строку, с помощью символа «'» -одинарная кавычка (буква э в латинском регистре) с) стандартной функцией vertcat(,,,) d) двоеточия «:» с шагом и транспонирования «'». Сцепление векторов. 1. Из нескольких вектор-столбцов можно составить один, используя квадратные скобки и разделяя исходные вектор-столбцы точкой с запятой: >> v1 = [1; 2]; v2 = [3; 4; 5]; v = [v1; v2] v = >> 2. Для сцепления вектор-строк также применяются квадратные скобки, но сцепляемые вектор-строки отделяются пробелами или запятыми: >> w1 = [1 2]; w2 = [3 4 5]; w = [w1 w2] w = 1 2 3 4 5
|
||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 667; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.198.214 (0.01 с.) |

 называется прямоугольная таблица, состоящая из n строк и m столбцов. Традиционно в математике эту таблицу заключают в круглые скобки. Например,
называется прямоугольная таблица, состоящая из n строк и m столбцов. Традиционно в математике эту таблицу заключают в круглые скобки. Например,  - матрица размерности
- матрица размерности  ;
; , т.е. состоит из одной строки и m столбцов, то ее называют вектор-строкой. Например,
, т.е. состоит из одной строки и m столбцов, то ее называют вектор-строкой. Например,  - матрица размерности
- матрица размерности  , т.е. вектор-строка.
, т.е. вектор-строка. , т.е. состоит n строк и одного столбца, то ее называют вектор-столбцом. Например,
, т.е. состоит n строк и одного столбца, то ее называют вектор-столбцом. Например,  - матрица размерности
- матрица размерности  , т.е. вектор - столбец.
, т.е. вектор - столбец.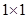 .
. с помощью
с помощью с помощью
с помощью


