
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Форматы вывода результата вычислений.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Встроенные математические функции MATLAB позволяют находить значения различных выражений. MATLAB предоставляет возможность управления форматом вывода результата. Вид, в котором выводится результаты вычислений, зависит от формата вывода, установленного в MATLAB. Далее объяснено, как задать основные форматы вывода. Числовые данные, с которыми мы пока будем оперировать в MATLAB, в памяти компьютера представлены вещественными переменными класса double. Это означает, что каждое вещественное число занимает 8 байтов в оперативной памяти и принимает по модулю значения из диапазона В таблице 2 представлены основные форматы вывода числовых данных с фиксированной (первый столбец) и плавающей (второй столбец) запятой. Формат rational (третий столбец) позволяет отображать числовые значения в виде подходящих рациональных дробей с минимально возможными числителями и знаменателями. При этом значение переменной x, хранящееся в памяти компьютера, не зависит от установленного формата вывода.
По умолчанию система использует формат short (укороченный). Замечание. Все промежуточные вычисления МАТЛАБ производит с двойной точностью double, независимо от того, какой формат вывода установлен. Упражнение 2. Форматы вывода результата вычислений. 1) сложите два числа 1/2 и 2/3 и определите формат полученного ответа; 2) перейдите в формат format rational (Можно кратко в format rat) и сложите числа 1/2 и 2/3, а также числа 0.3 и 0.6, 3) выберите в меню File → Preferences → Command Window в открывшемся окне Command Window Preferences в разделе Text display выберите заголовок Numeric format и снова сложите числа 1/2 и 2/3, а также числа 0.3 и 0.6 затем снова через Preferences переведите вывод данных в формат short.
Символьные переменные. Работа с алгебраическими выражениями. Команда >> syms a b c d (переменные записываются через пробел) позволяет работать с символьными переменными как с числами, то есть мы можем работать с алгебраическими выражениями: Пример. Работа с алгебраическими выражениями, с символьными переменными. Введите >> clear all >> f=(x+1)*(x-1) ??? Undefined function or variable 'x'. МАТЛАБ выдал сообщение об ошибке. Теперь введите >> syms x >> f=(x+1)*(x-1) f = (x - 1)*(x + 1) МАТЛАБ вывел алгебраическое выражение. Посмотрите в help команды-simplifications (упрощения): как делать различные преобразования в алгебраических выражениях. Введите >> f=collect(f) f = x^2 - 1 Ответьте в отчете на вопрос, что сделала команда «collect» с выражением f?
Пример. Работа с алгебраическими выражениями. Подстановка чисел. Теперь присвоим x какое-нибудь число: >>x = 2 снова вызовем f >> f f = (x+1)*(x-1) ничего не изменилось, но если набрать заново алгебраическое выражение f=(x+1)*(x-1) (можно просто выбрать данную команду при помощи стрелок) >> f=(x+1)*(x-1) f = 3 Мы получим значение функции f=3, при x = 2.
Пример. Упрощение алгебраических выражений. При помощи различных команд simplifications (упрощения) записать различные формулы сокращенного умножения: разность квадратов; квадрат суммы, разности; куб суммы, разности; разность кубов, сумма кубов. В качестве символьных переменных можно выбрать не только буквы, но и числа. Например, если нужно раскрыть скобки в выражении >> (sqrt(2)+sqrt(6))^2 ans = 14.9282 вычисляет значение выражения Теперь введем >> a=sym(sqrt(6)) a = 6^(1/2) >> b=sym(sqrt(2)) b = 2^(1/2) >> (a+b)^2 ans = (2^(1/2) + 6^(1/2))^2
>> w=simple(ans) w = 4*3^(1/2) + 8 Теперь мы раскрыли скобки и привели подобные слагаемые и получили ответ в радикалах: А для того чтобы узнать его примерное значение введем >> 4*3^(1/2) + 8 ans = 14.9282
Посмотрите через help функцию sym. Команда sym позволяет вводить ограничения на свойства переменных: Решим уравнение: >> clear all solve('x^4-1=0') ans = -1 -i i
Уравнение имеет действительные и комплексные корни. Теперь введем ограничение на переменную: x – вещественное (действительное) число. >> x = sym('x', 'real') x = x >> solve('x^4-1=0') ans = -1 Выведены только вещественные значения корней уравнения.
Массивы в MATLAB.
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 3895; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.21.70 (0.009 с.) |

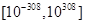 . Количество значащих цифр при этом достигает 16 - 17. Именно с такой точностью MATLAB выполняет все вычисления. Однако при отображении всех результатов на экране часть значащих цифр отбрасывается в соответствии с установленным форматом вывода. Отображаемые значения округляются по общепринятым в математике правилам.
. Количество значащих цифр при этом достигает 16 - 17. Именно с такой точностью MATLAB выполняет все вычисления. Однако при отображении всех результатов на экране часть значащих цифр отбрасывается в соответствии с установленным форматом вывода. Отображаемые значения округляются по общепринятым в математике правилам.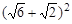 , то ввод
, то ввод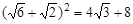 .
.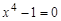 .
.


