Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Системы нечеткого логического выводаСодержание книги
Поиск на нашем сайте Нечеткая логика (НЛ) подразумевает проведение операции нечеткого логического вывода, основой которого является база правил, а также функция принадлежности лингвистических терм. Результатом является четкое значение переменной. Нечетким логическим выводом называется аппроксимация зависимости Для того что бы выполнить нечеткий логический вывод необходимы следующие условия: [53] - должно существовать как минимум одно правило для каждого лингвистического терма выходной переменной; - для любого терма входной переменной должно быть хотя бы одно правило, в которой этот терм используется в качестве предпосылки; - между правилами не должно быть противоречий и корреляции. На рисунке 1.7. изображена последовательность действий при использовании процесса нечеткого логического вывода.
Рисунок 1.7 – Последовательность действий при использовании процесса нечеткого логического вывода Нечеткий логический вывод занимает центральное место в нечеткой логике и системах нечеткого управления. Этот процесс представляет собой процедуру или алгоритм получения нечетких заключений на основе нечетких условий или предпосылок. Системы нечеткого логического вывода являются частным случаем продукционных нечетких систем, в которых условия и заключения, отдельных правил формулируются в форме нечетких высказываний относительно значений тех или иных лингвистических переменных. Разработка и применение систем нечеткого логического вывода включают в себя несколько этапов, реализация которых выполняется с помощью рассмотренных ранее основных положений нечетких множеств. Входные переменные, поступающие на вход системы нечеткого логического вывода, являются информацией, которая замеряется каким-либо образом. Эти переменные есть реальные переменные процесса управления. Управляющие переменные системы управления формируются на выходе системы нечеткого логического вывода.
ПРАВИЛО<#>: ЕСЛИ “β1 есть α1”,ТО “β2 есть α2” Здесь нечеткое высказывание “β1 есть α1” представляет собой условие данного правила нечеткой продукции, а нечеткое высказывание “β2 есть α2” – нечеткое заключение данного правила, которые сформулированы в терминах нечетких лингвистических высказываний. При этом считается, что β1 ≠ β2. Основные этапы нечеткого логического вывода и особенности каждого из них более подробно рассмотрены ниже: [50] 1) Формирование базы правил. База правил систем нечеткого логического вывода предназначена для формального представления эмпирических знаний или знаний экспертов в той или иной проблемной области и представляет собой совокупность правил нечетких продукций вида: ПРАВИЛО_1: ЕСЛИ “Условие _1”,ТО “Заключение_1”(F1)
… ПРАВИЛО_n: ЕСЛИ “Условие _n”,ТО “Заключение_n”(Fn) Здесь Fi (i принадлежит {1, 2, …, n}) есть коэффициенты определенности или весовые коэффициенты соответствующих правил, которые могут принимать значения из интервала [0;1]. Если не указано иначе, то Fi=1. Таким образом, база правил считается заданной, если для нее определено множество правил нечетких продукций, множество входных лингвистических переменных и множество выходных лингвистических переменных. 2) Фаззификация (введение нечеткости) является процессом и процедурой нахождения значений функций принадлежности нечетких множеств (термов) на основе обычных (четких) исходных данных. После завершения этого этапа для всех входных переменных должны быть определены конкретные значения функций принадлежности по каждому из лингвистических термов, которые используются в подусловиях базы правил системы нечеткого логического вывода. 3) Агрегирование представляет собой процедуру определения степени истинности условий по каждому из правил системы нечеткого логического вывода. Если условие правила имеет простую форму, то степень его истинности равна соответствующему значению принадлежности входной переменной к терму, используемому в данном условии. В том случае, когда условие состоит из нескольких подусловий вида:
ПРАВИЛО<#>: ЕСЛИ “β1 есть α1” ИЛИ “β2 есть α2”,,ТО “β3 есть ν”, то определяется степень истинности сложного высказывания на основе известных значений истинности подусловий. При этом используются соответствующие формулы для выполнения нечеткой конъюнкции и нечеткой дизъюнкции: §
§
4) Активизация есть процесс нахождения степени истинности каждого из подзаключений правил нечетких продукций. До начала этого этапа предполагаются известными степень истинности и весовой коэффициент (Fi) для каждого правила. Далее рассматривается каждое из заключений правил системы нечеткого логического вывода. Если заключение правила представляет собой одно нечеткое высказывание, то степень его истинности равна алгебраическому произведению соответствующей степени истинности условия на весовой коэффициент. Когда заключение состоит из нескольких подзаключений вида:
ПРАВИЛО<#>: ЕСЛИ “β1 есть α1” ТО “β2 есть α2” ИЛИ “β3 есть ν”, то степень истинности каждого из подзаключений равна алгебраическому произведению соответствующего значения степени истинности условия на весовой коэффициент. После нахождения множества Сi={c1, c2, …, cn} степеней истинности каждого из подзаключений определяются функции принадлежности каждого из них для рассматриваемых выходных лингвистических переменных. Для этого используется один из следующих методов: · Min-активизация: μ’(y)=min{Ci, μ(y)}; · Prod- активизация: μ’(y)=Ci*μ(y); · Average- активизация: μ’(y)=0.5*(Ci+μ(y)), где μ’(y) – функция принадлежности терма, который является значением некоторой выходной переменной yj, заданной на универсуме Y. 5) Аккумуляция является процессом нахождения функции принадлежности для каждой из выходных лингвистических переменных. Цель аккумуляции – объединить все степени истинности заключений (подзаключений) для получения функции принадлежности каждой из выходных переменных. Причина необходимости этого этапа заключается в том, что подзаключения, относящиеся к одной и той же выходной лингвистической переменной, принадлежат различным правилам системы нечеткого логического вывода. Объединение нечетких множеств Ci производят с помощью формулы:
где
6) Дефаззификация (приведение к четкости) представляет собой процедуру нахождения обычного (четкого) значения для каждой из выходных лингвистических переменных. Цель заключается в том, чтобы, используя результаты аккумуляции всех выходных лингвистических переменных, получить обычное количественное значение каждой из выходных переменных, которое может быть использовано специальными устройствами, внешними по отношению к системе нечеткого логического вывода. Для выполнения численных расчетов на завершающем данном этапе могут быть использованы следующие методы дефаззификации (рисунок 1.8):
Centroid - центр тяжести; Bisector - медиана; SOM (Smallest Of Maximums) - наименьший из максимумов; LOM (Largest Of Maximums) - наибольший из максимумов; MOM (Mean Of Maximums) - центр максимумов. Рисунок 1.8 – Основные методы дефаззификации
где Для дискретного варианта:
где
где
где 4. Метод “наименьший из максимумов” предполагает определение наименьшего значения, при котором достигается максимум нечеткого множества выходной переменной:
где 5. Метод “ наибольший из максимумов ”
где
|
||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1923; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.113 (0.007 с.) |

 с помощью нечеткой базы знаний и операций над нечеткими множествами.
с помощью нечеткой базы знаний и операций над нечеткими множествами.
 Таким образом, системы нечеткого логического вывода предназначены для преобразования значений входных переменных процесса управления в выходные переменные на основе использования нечетких правил продукций. Простейший вариант правила нечеткой продукции, который наиболее часто используется в системах нечеткого логического вывода, записывается в форме:
Таким образом, системы нечеткого логического вывода предназначены для преобразования значений входных переменных процесса управления в выходные переменные на основе использования нечетких правил продукций. Простейший вариант правила нечеткой продукции, который наиболее часто используется в системах нечеткого логического вывода, записывается в форме: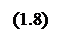 ПРАВИЛО_2: ЕСЛИ “Условие _2”,ТО “Заключение_2”(F2)
ПРАВИЛО_2: ЕСЛИ “Условие _2”,ТО “Заключение_2”(F2) ПРАВИЛО<#>: ЕСЛИ “β1 есть α1” И “β2 есть α2”,ТО “β3 есть ν”, или
ПРАВИЛО<#>: ЕСЛИ “β1 есть α1” И “β2 есть α2”,ТО “β3 есть ν”, или Нечеткая логическая конъюнкция (И)
Нечеткая логическая конъюнкция (И)
 Нечеткая логическая дизъюнкция (ИЛИ)
Нечеткая логическая дизъюнкция (ИЛИ)
 ПРАВИЛО<#>: ЕСЛИ “β1 есть α1” ТО “β2 есть α2” И “β3 есть ν”, или
ПРАВИЛО<#>: ЕСЛИ “β1 есть α1” ТО “β2 есть α2” И “β3 есть ν”, или
 ,
, – модальное значение (мода) нечеткого множества, соответствующего выходной переменной после аккумуляции, рассчитываемое по формуле:
– модальное значение (мода) нечеткого множества, соответствующего выходной переменной после аккумуляции, рассчитываемое по формуле:


 1. Метод центра тяжести (Centre of Gravity) считается одним из самых простых по вычислительной сложности, но достаточно точным методом. Расчет производится по формуле:
1. Метод центра тяжести (Centre of Gravity) считается одним из самых простых по вычислительной сложности, но достаточно точным методом. Расчет производится по формуле:
 - это результат дефаззификации (точное значение выходной переменной);
- это результат дефаззификации (точное значение выходной переменной);  – границы интервала носителя нечеткого множества выходной переменной;
– границы интервала носителя нечеткого множества выходной переменной;  - функция принадлежности нечеткого множества, соответствующего выходной переменной после этапа аккумуляции.
- функция принадлежности нечеткого множества, соответствующего выходной переменной после этапа аккумуляции.

 – число элементов
– число элементов  в области
в области  для вычисления «центра тяжести».
для вычисления «центра тяжести».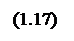 2. Метод центра площади (Centre of Area):
2. Метод центра площади (Centre of Area):
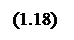 3. Метод “ центр максимумов ” вычисляется по формуле:
3. Метод “ центр максимумов ” вычисляется по формуле:
 - базовое пространство выходной переменной,
- базовое пространство выходной переменной,  ;
;