Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Квадратурний метод розв'язку інтегральних рівнянь ВольтерраСодержание книги
Поиск на нашем сайте
Оскільки лінійні інтегральні рівняння Вольтера мають єдиний безперервний розв'язок при будь-яких значеннях параметра Враховуючи, що рівняння Вольтера можна вважати рівнянням Фредгольма: с ядром Для знаходження розв'язку розглянутого рівняння скористаємося результатами підрозділу 5.3. Введемо в розгляд часову сітку
З (5.14) видно, що невідомі значення
Приклад 5.2. Інтегральне рівняння
Має точний розв'язок Знайдемо чисельний розв'язок цього рівняння, використовуючи метод трапецій, і порівняємо його з точним.
a=0; b=2.5; h=0.05; n=(b-a)/h+1; x(1)=a; y(1)=f(a); for i=2:n x(i)=a+(i-1)*h; g=f(x(i)); for j=1:i-1 if (j==1) c=0.5; else c=1; end; g=g+h*c*K(x(i),x(j))*y(j); end; y(i)=g/(1-h/2*K(x(i),x(i))); ty(i)=exp(x(i))*(cos(exp(x(i)))-p(x(i))*sin(exp(x(i)))); end; plot(x,y,x,ty,'.'); grid on; Функції: function y=f(x) y=(1-x*exp(2*x))*cos(1)-exp(2*x)*sin(1);
function z=K(x,t) z=1-(x-t)*exp(2*x);
Рисунок 5.1 – Точний й наближений розв'язок прикладу 5.2. Завдання до лабораторної роботи Завдання 5.1. Методом послідовних наближень (вручну й у пакеті MATLAB) і квадратурним методом знайти розв'язок рівнянь Фредгольма 2-го роду, попередньо переконавшись, що умова (7.6) виконана. Розрахунки квадратурним методом провести з двома різними кроками і отримати оцінку погрішності за правилом Рунге. 1. 3. 4. 6. 7. 8. 9. 10. Завдання 5.2. Методом послідовних наближень (вручну й у пакеті MATLAB) і квадратурним методом знайти розв'язок рівнянь Вольтерра 2-го роду. 1. 3. 5. 7. 9. 10.
5.8 Контрольні питання
МЕТОДИ АПРОКСИМУЮЧИХ ФУНКЦІЙ РОЗВ'ЯЗКУ ІНТЕГРАЛЬНИХ РІВНЯНЬ
Загальний підхід Розв'язок інтегрального рівняння
будемо шукати у вигляді розкладання в ряд по базисних функціях
тут Збіжність наближеного розв'язку Підставимо
Для визначення коефіцієнтів Метод колокацій Виберемо вузли
Розв'язавши систему, одержуємо шукані коефіцієнти Метод найменших квадратів Виберемо вузли
Відомо, що мінімум досягається в точці, у якій частинні похідні по
Підставимо в останнє рівняння вираз для нев’язки (8.2) і значення її похідної. Одержимо таку систему:
де
Система є лінійною алгебраїчною системою відносно невідомих коефіцієнтів
Метод Гальоркіна Відомо [6,8], що мінімум нев’язки досягається тоді, коли нев’язка ортогональна координатним функціям. Звідси одержуємо систему рівнянь для невідомих коефіцієнтів розкладання (6.1):
Підставивши вираження для нев’язки (8.2), одержимо
Приведемо останню систему до стандартного вигляду:
Позначимо
і запишемо систему відносно Система є лінійною алгебраїчною системою і має єдиний розв'язок, що обумовлено вибором координатних функцій. Розв'язавши систему, одержуємо рішення інтегрального рівняння у вигляді (6.1). Приклад 6.1. Методом Гальоркіна розв'язати інтегральне рівняння
Рішення. Оберемо такі координатні функції:
Тобто будемо шукати рішення такого виду:
Обчислемо нев’язку
Згідно методу Гальоркіна запишемо умови ортогональності невязки до координатних функцій:
Обчислимо інтеграли і отримаємо таку систему рівнянь:
розвязком якої є значення
Таким чином, ми одержали наближене рішення інтегрального рівняння: Перевіримо цей результат, використовуючи Symbolic Tools системи MatLab. % метод апроксимуючих функцій розв'язання інтегрального % рівняння syms x t fi f K; % Задаємо праву частину рівняння та координатні функції fun=1;n=3;a=-1; b=1;lambda=1; fi(1)=1; fi(2)=x; fi(3)=x^2; f(2)=t; f(3)=t^2; f(1)=1; K=x*t+x*x; % Обчислюємо коефіцієнти системи лінійних рівнянь for k=1:n for i=1:n aa=int(fi(i)*fi(k),'x',a,b); ab=int(K*f(i),'t',a,b); ak=-lambda*int(fi(k)*ab,'x',a,b); A(k,i)=aa+ak; g(k,i)=eval(A(k,i)); end; B(k)=int(fi(k)*fun,'x',a,b); h(k)=eval(B(k)); end; A B c=g\h' % розв’язуємо систему рівнянь % Будуємо функцію - наближений розв'язок задачі u=c(1)*fi(1); for i=2:n u=u+c(i)*fi(i); % розв'язок у символьному вигляді end; u % Обчислимо таблицю значень функції розв'язку hx=0.01; for i=1:100 x=(i-1)*hx; y(i)=x; zz(i)=eval(u); end; plot(y,zz,'.') % будуємо графік grid on Результат роботи програми (порівняйте з ручним розрахунком!): A = [ 2/3, 0, 2/9] [ 0, 2/9, 0 ] [ -2/15, 0, 2/15] B = [ 2, 0, 2/3] c = 1.0000 0 6.0000 u = 6*x^2 + 1
Рисунок 6.1 – Графік рішення прикладу 6.1
|
||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 620; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.221.131 (0.011 с.) |

 , при знаходженні чисельного розв'язку рівняння Вольтерра другого роду можна покласти
, при знаходженні чисельного розв'язку рівняння Вольтерра другого роду можна покласти  .
. ,
, . (5.13)
. (5.13) , що складається з
, що складається з  вузлів, і виберемо конкретну квадратурну формулу з вагами
вузлів, і виберемо конкретну квадратурну формулу з вагами  , тоді наближений розв'язок інтегрального рівняння має вид (7.9). Складемо СЛАУ, аналогічну системі (7.10), яка в силу властивостей ядра інтегрального рівняння (7.13) вироджується в трикутну:
, тоді наближений розв'язок інтегрального рівняння має вид (7.9). Складемо СЛАУ, аналогічну системі (7.10), яка в силу властивостей ядра інтегрального рівняння (7.13) вироджується в трикутну: (5.14)
(5.14) знаходяться послідовними обчисленнями по формулах:
знаходяться послідовними обчисленнями по формулах: ,
,  ,.
,.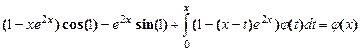
 .
.
 . 2.
. 2.  .
. .
. . 5.
. 5.  .
.
 .
. .
. .
.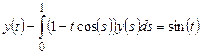 .
. ,
,  . 2.
. 2.  ,
, 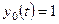 .
. ,
,  . 4.
. 4.  ,
,  .
. ,
,  ,
,  ,
,  ,
, 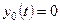 .
. ,
,  ,
, 
 , які є частиною повної системи лінійно незалежних функцій:
, які є частиною повної системи лінійно незалежних функцій: , (6.1)
, (6.1)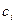 - невідомі параметри.
- невідомі параметри. до точного при
до точного при 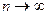 забезпечується вибором системи координатних функцій.
забезпечується вибором системи координатних функцій. (6.2)
(6.2) й зажадаємо, щоб нев’язка дорівнювала нулю у вузлах. В результаті одержимо систему лінійних алгебраїчних рівнянь щодо коефіцієнтів
й зажадаємо, щоб нев’язка дорівнювала нулю у вузлах. В результаті одержимо систему лінійних алгебраїчних рівнянь щодо коефіцієнтів 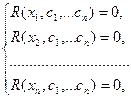

 .
. (
( ) і зажадаємо, щоб коефіцієнти
) і зажадаємо, щоб коефіцієнти 

 ,
,

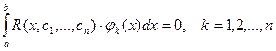 .
.

 ,
, ,
, .
. .
.


 ,
, .
. . Переконайтесь самостійно, що це рішення є точним.
. Переконайтесь самостійно, що це рішення є точним.