
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Різницеві схеми підвищеної точності. Схема Кранка-НікольсонаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Різницеві схеми підвищеної точності будуються за шаблонами, які використовують більше точок, що дозволяє підвищити порядок апроксимації диференціальної задачі різницевою схемою. Схема Кранка-Нікольсона будується за шеститочковим шаблоном і має вигляд:
Порядок апроксимації цієї схеми Покажемо, чому апроксимація за часом має другий порядок точності. Для цього розкладемо функцію
Звідки отримуємо
Приклад 3.1 – продовження. Знайдемо рішення задачі прикладу 3.1 за схемою півищеної точності Кранка-Нікольсона. Программа, що виконує розрахунки: %_5_1_nejavn n=6;hx=0.2; m=n; ht=0.02; u=zeros(m,n); a=1; sig=a^2*ht/hx^2/2; x=0:hx:1; u(1,:)=abs(2*x-1); t=0:ht:1; v=abs(2*t-1); plot(t,v, 'LineWidth',2); hold on; grid on % формуємо матрицю системи for i=1:m-1 a=zeros(n,3);y=zeros(n,1); a(1,2)=1; b(1)=1; a(n,2)=1; b(n)=1; for j=2:n-1 a(j,1)=-sig; a(j,2)=(1+2*sig); a(j,3)=-sig; b(j)=sig*u(i,j-1)+(1-2*sig)*u(i,j) end % розвязуємо систему методом прогону y=progonka(n,a,b); u(i+1,:)=y; end
% графіки розподілу температури з кроком за часом 0.02 plot(x,u(2,:),'--o','LineWidth',2) plot(x,u(3,:),':s','LineWidth',2) plot(x,u(4,:),'-.*','LineWidth',2) plot(x,u(5,:),'--x','LineWidth',2) plot(x,u(6,:),'-->','LineWidth',2) u(1:m,1:n)
Розв'язок задачі з кроками u = 1.0000 0.6000 0.2000 0.2000 0.6000 1.0000 1.0000 0.6276 0.3655 0.3655 0.6276 1.0000 1.0000 0.6837 0.4816 0.4816 0.6837 1.0000 1.0000 0.7370 0.5731 0.5731 0.7370 1.0000 1.0000 0.7825 0.6477 0.6477 0.7825 1.0000 1.0000 0.8203 0.7092 0.7092 0.8203 1.0000. Як бачимо, цей розв'язок більш точний ніж розв'язок за явною схемою з тими ж кроками. Розрахунок з кроками в 2 рази менше дає такі результати: u = 1.0000 0.6000 0.2000 0.2000 0.6000 1.0000 1.0000 0.6211 0.3539 0.3539 0.6211 1.0000 1.0000 0.6782 0.4733 0.4733 0.6782 1.0000 1.0000 0.7336 0.5679 0.5679 0.7336 1.0000 1.0000 0.7807 0.6450 0.6450 0.7807 1.0000 1.0000 0.8197 0.7082 0.7082 0.8197 1.0000 Погрішність останнього результату дорівнює
що складає 1,4% від значення функції. Зауважимо, що ми одержали значно кращий результат, ніж за явною схемою, навіть обравши крок за часом в два рази більше. Графік останнього розв'язку наведений на рис. 3.5.
Рисунок 5.5 – Графіки розв'язку прикладу 5.1 за неявною схемою
Задачі для самостійного розв'язку на практиці Задача 3.1. Перевірити, що функція Задача 3.2. Розв'язати задачу розподілу тепла в стрижні довжини 1, тобто розв'язати рівняння початковій умові: граничних умовах Розрахунки виконати до моменту часу
Завдання до лабораторної роботи Завдання 3.1. Використовуючи метод сіток одержати розв'язок змішаної задачі для диференціального рівняння параболічного типу Завдання 3.2. Знайти наближений розв'язок задачі завдання 3.1 за допомогою неявної різницевої схеми. Порівняти отримані розв'язки й об'єм обчислень, необхідних для одержання розв'язку з тою ж точністю. Варіанти індивідуальних завдань 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. Завдання 3.3. Розв'язати двовимірну крайову задачу:
За допомогою PDE Tools пакета MATLAB. Розв'язок задачі вивести у вигляді анімації. Варіанти індивідуальних завдань
3.7 Контрольні питання Якого виду граничні умови використовуються в задачах параболічного типу? 2. Які види шаблонів використовуються в методі сіток у задачах параболічного типу? Яким чином будують на цих сітках різницеві апроксимації? 3. Опишіть метод прогону і його роль у розв'язку задач із ДРЧП. 4. З яких міркувань вибирають крок сітки в методі сіток? 5. У яких випадках може виникати нестійкість розв'язку задачі? Як впливає вибір параметрів сітки на стійкість? 6. Що розуміють під збіжністю процесу розв'язку задачі? 7. Що таке різницеві схеми підвищеної точності і які шаблони при цьому використовуються? 8. Як можна одержати апостеріорні оцінки погрішності отриманого розв'язку та уточнити розв'язок? 4МЕТОД СІТОК РОЗВ'ЯЗКУ КРАЙОВИХ ЗАДАЧ ДЛЯ ХВИЛЬОВИХ РІВНЯНЬ Постановка задачі Класичним прикладом рівняння гіперболічного типу є хвильове рівняння, яке в області
Дане рівняння описує, зокрема, процес малих поперечних коливань струни (рис. 4.1). В цьому випадку
Рисунок 4.1 - Модель струни В задачах для хвильового рівняння крім початкового розподілу шуканої функції задається ще й розподіл початкової швидкості переміщення (початкові умови):
Також задаються граничні умови:
причому якщо кінці струни жорстко закріплені, то
Для розв'язку задачі методом кінцевих різниць побудуємо прямокутну сітку (рис. 4.2), вузли якої визначаються формулами: Значення Явна схема Замінимо частинні похідні в рівнянні (4.1) їх кінцево-різницевими апроксимаціями й підставимо їх у рівняння коливання. Одержимо:
Тут використовується п’яти точковий шаблон, представлений на рис. 4.2. Отримане рівняння дозволяє виразити значення функції
Позначимо
У якості граничних умов по Алгоритм обчислень за явною схемою реалізується такою послідовністю дій. 1. Визначимо деформацію стрижня в моменти
Похибка формули (4.3) 2. Для одержання розв'язку при Схема (4.2)-(4.3) дає порядок апроксимації
Відповідне різницеве рівняння запишеться таким чином:
Звідки
Виключаємо з останнього рівняння
Різницева схема (4.2), (4.4) апроксимує диференціальну задачу з порядком Явна схема умовно стійка. Це означає, що при розв'язку гіперболічного рівняння за явною схемою слід обирати крок по Приклад 4.1. Знайдіть розв'язок задачі для хвильового рівняння, яке описує коливання струни із закріпленими кінцями
де Розв'язок. Побудуємо сітку, як показано на рис. 4.3. Тобто оберемо кроки по Різницеве рівняння коливання струни
(з урахуванням
Схема стійка, якщо Із початкових умов одержимо:
Тому що струна закріплена на кінцях, маємо
Так як Підрахуємо значення для
Аналогічно обчислюємо для інших значень
Рисунок 4.3 – Просторово-тимчасова сітка прикладу 4.1. Розв'яжемо задачу з кроком вдвічі менше за просторовою змінною Різницеве рівняння стане таким:
Для виконання розрахунків складемо програму.
function u=giperb6_1(hx,ht) % розрахунок коливання струни за явною схемою % кінцевий час Т=6 L=10; T=6; n=L/hx+1; m=T/ht+1; u=zeros(m,n); a=ht^2/hx^2; kt=2/ht;kx=2/hx; x=0:hx:L; % початкові умови for i=1:n if x(i)<0.6*L u(1,i)=x(i); else u(1,i)=1.5*(L-x(i)); end; end u(2,1)=u(1,1); u(2,n)=u(1,n); for i=2:n-1 u(2,i)=0.5*(a*u(1,i-1)+2*(1-a)*u(1,i)+a*u(1,i+1)); end plot(x,u(1,:),'LineWidth',3); hold on; grid on % наступні положення струни за часом for i=2:m u(i+1,1)=0; u(i+1,n)=0; for j=2:n-1 u(i+1,j)=a*(u(i,j+1)+u(i,j-1))+2*u(i,j)*(1-a)- end end % графіки форми струни з кроками hx=2 ht=2 plot(x,u(kt+1,:),'--o','LineWidth',2) plot(x,u(2*kt+1,:),':s','LineWidth',2) plot(x,u(3*kt+1,:),'-.*','LineWidth',2) u(1:kt:m,1:kx:n) Графік розв'язку, отриманий із кроком Значення функції u – форми струни- - для моментів часу 0, 2, 4 та 6 та для координат х=0,2,4,6,8,10 такі: u= 0 2.0000 4.0000 6.0000 3.0000 0 0 2.0000 3.8730 3.2852 2.8730 0 0 1.8141 1.4222 1.0606 0.4232 0 0 -0.4521 -0.8588 -1.4118 -1.6334 0 Порівняємо значення для t=4 (третя строка матриці u) зі значеннями, що отримані ручним розрахунком, та обчислимо погрішність за правилом Рунге:
Погрішність розв'язку, як видно, досить велика. Це говорить про необхідність зменшення кроків по просторовій координаті й за часом. Розрахунки із кроком
Рисунок 4.4 – Розв'язок задачі 6.1 із кроками
Рисунок 4.5 – Розв'язок задачі 6.1 із кроком Значення функції u – форми струни- - для моментів часу 0, 2, 4 та 6 та для координат х=0,2,4,6,8,10 такі: u = 0 2.0000 4.0000 6.0000 3.0000 0 0 2.0000 3.9070 3.5303 2.9070 0 0 1.8720 1.5255 0.9435 0.5255 0 0 -0.5609 -0.9490 -1.4680 -1.7974 0 Абсолютна погрішність для часу t=4 цього рішення Неявна схема Неявні схеми для рівняння (4.1) рекомендують використовувати тому, що вони є безумовмо стійкими і дозволяють надійно отримати розв'язок задачі навіть з достатньо великими кроками за часом. Найпростішим є п'яти точковий шаблон, який наближає другу похідну по х для часу Розглянемо для рівняння (4.1) неявну п'яти точкову схему й запишемо відповідне різницеве рівняння:
Після перетворень та враховуючи граничні умови, отримуємо систему лінійних алгебраїчних рівнянь для кожного часового шару, починаючи з третього. Значення розв'язку на перших двох шарах обчислюємо з початкових умов та за формулою (4.4). Систему можна розв'язувати методом прогону, який буде стійким, тому що має місце діагональна перевага. Система різницевих рівнянь для неявної схеми:
де Схема є абсолютно стійкою. Кроки по координаті та часу обирають тільки з умови досягнення необхідної точності. Приклад 4.1 – продовження. Розв'яжемо задачу цього прикладу за неявною схемою. Складемо програму, що формує матрицю системи лінійних алгебраїчних рівнянь, та розв'язує систему методом прогону. У матриці буде тільки 3 стовпчики, у яких будемо зберігати тільки три ненульових діагоналі матриці. function u=giperb_4_1_nejavn1(hx,ht) % розв’язання задачі 6.1 за неявною схемою L=10; n=L/hx+1; m=6/ht+1; kt=2/ht;kx=2/hx; u=zeros(m,n); sig=ht^2/hx^2; x=0:hx:L; % початкові умови for i=1:n if x(i)<0.6*L u(1,i)=x(i); else u(1,i)=1.5*(L-x(i)); end; end plot(x,u(1,:),'LineWidth',3); hold on; grid on u(2,1)=u(1,1); u(2,n)=u(1,n); for i=2:n-1 u(2,i)=0.5*(sig*u(1,i-1)+ end % наступні положення струни за часом for i=2:m-1 a=zeros(n,3);y=zeros(n,1); a(1,2)=1; b(1)=0; a(n,2)=1; b(n)=0; for j=2:n-1 a(j,1)=sig; a(j,2)=-(1+2*sig); a(j,3)=sig; b(j)=-2*u(i,j)+u(i-1,j); end y=progonka(n,a,b); u(i+1,:)=y; end % графіки форми струни з кроками hx=2 ht=2 plot(x,u(kt+1,:),'--o','LineWidth',2) plot(x,u(2*kt+1,:),':s','LineWidth',2) plot(x,u(3*kt+1,:),'-.*','LineWidth',2) u(1:kt:m,1:kx:n) Отримаємо такі результати (графіки форми струни наведені на рис. 4.6): >> u=giperb_4_1_nejavn1(0.5,0.5) u = 0 2.0000 4.0000 6.0000 3.0000 0 0 1.9804 3.6691 3.8087 2.6699 0 0 1.4608 1.7735 1.3185 0.8451 0 0 -0.1612 -0.6514 -1.0489 -0.9819 0 Зверніть увагу, що крок за часом в розрахунку за неявною схемою обраний в 2 рази більше, ніж за явною, він не впливає на стійкість результату. Щоб обчислити апостеріорну оцінку погрішності останнього результату, проведемо розрахунок з кроками в 2 рази більше, тобто >> u=giperb_4_1_nejavn1(1,1) u = 0 2.0000 4.0000 6.0000 3.0000 0 0 1.9534 3.6741 3.7650 2.6807 0 0 1.3789 1.9505 1.6581 1.1057 0 0 0.0782 -0.2393 -0.5468 -0.5111 0 Погрішність рішення для часу t=4 Як бачимо, розрахунки за неявною схемою дозволяють обирати більший крок за часом та отримувати результат з майже такою ж погрішністю, ніж за явною схемою.
Рисунок 4.6 – Розв'язок задачі 4.1 за неявною схемою із кроками
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 480; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.23.138 (0.015 с.) |

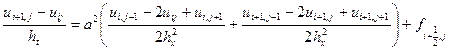
 . Схема є абсолютно стійкою, тобто кроки
. Схема є абсолютно стійкою, тобто кроки  та
та  обираються тільки з умов досягнення необхідної точності.
обираються тільки з умов досягнення необхідної точності. в ряд Тейлора в точці
в ряд Тейлора в точці  . Позначимо
. Позначимо  .
.

 .
.
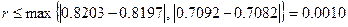 ,
,
 є розв'язком рівняння
є розв'язком рівняння  для кожного позитивного числа
для кожного позитивного числа 
 при
при ,
, .
. . Розв'язати по явній і неявній схемі й порівняти результати.
. Розв'язати по явній і неявній схемі й порівняти результати. (рівняння теплопровідності) при заданих початкових і граничних умовах
(рівняння теплопровідності) при заданих початкових і граничних умовах  ,
,  ,
,  , де
, де  . Розв'язок виконати при
. Розв'язок виконати при  , крок за часом підібрати з умови стійкості. Знайти наближений розв'язок задачі за допомогою явної різницевої схеми. Повторити розрахунки з половинним кроком по координаті, вибравши відповідний крок за часом, зрівняти отримані результати й одержати оцінку погрішності розв'язку.
, крок за часом підібрати з умови стійкості. Знайти наближений розв'язок задачі за допомогою явної різницевої схеми. Повторити розрахунки з половинним кроком по координаті, вибравши відповідний крок за часом, зрівняти отримані результати й одержати оцінку погрішності розв'язку. ,
,  ,
,  .
. ,
,  ,
,  .
. ,
,  ,
, 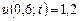 .
.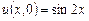 ,
,  ,
,  .
. ,
,  .
. ,
,  ,
,  .
. ,
,  ,
,  .
. ,
,  ,
,  .
.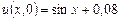 ,
,  ,
,  .
. ,
,  ,
,  .
. ,
,  ,
,  .
. ,
,  ,
,  .
. ,
,  ,
,  .
. ,
,  ,
,  .
. ,
,  ,
,  .
. ,
,  ,
,  ,
,  .
. ,
,  ,
,  .
. ,
, 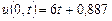 ,
, 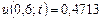 .
. ,
,  ,
,  .
. ,
,  ,
,  ,
,  .
.
 , см
, см
 , см
, см
 , хв
, хв












 має вигляд:
має вигляд: , (4.1)
, (4.1) – поперечні переміщення (коливання) струни,
– поперечні переміщення (коливання) струни, 
 ,
,  ,
, ,
,  ,
, .
.
 ,
,  ,
,  ,
,  .
. на лівій, правій і нижній границях сітки відомі з початкових і граничних умов.
на лівій, правій і нижній границях сітки відомі з початкових і граничних умов. .
. в момент часу
в момент часу  через значення функції в попередні моменти часу:
через значення функції в попередні моменти часу: .
.
 , приведемо подібні в останньому рівнянні і отримаємо розрахункову формулу для явної схеми:
, приведемо подібні в останньому рівнянні і отримаємо розрахункову формулу для явної схеми: (4.2)
(4.2) можуть використовуватися будь-які умови, що описують спосіб закріплення струни. Наприклад, жорстке закріплення припускає нульове зрушення на кінцях струни:
можуть використовуватися будь-які умови, що описують спосіб закріплення струни. Наприклад, жорстке закріплення припускає нульове зрушення на кінцях струни:  . За часом
. За часом  у якості початкових умов задамо при
у якості початкових умов задамо при  вхідну деформацію струни й початкову швидкість
вхідну деформацію струни й початкову швидкість  .
. . Для
. Для  деформацію визначимо за допомогою другої початкової умови, що задає швидкість
деформацію визначимо за допомогою другої початкової умови, що задає швидкість  при
при 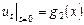 , тоді
, тоді  , отже
, отже (4.3)
(4.3) .
. використовуємо формулу (4.2).
використовуємо формулу (4.2). . Але порядок апроксимації можна збільшити. Для цього введемо фіктивний часовий шар з вузлами
. Але порядок апроксимації можна збільшити. Для цього введемо фіктивний часовий шар з вузлами  , що лежатиме за межами розрахункової області. Значення сіткової функції на цьому шарі позначимо
, що лежатиме за межами розрахункової області. Значення сіткової функції на цьому шарі позначимо  ,
,  . Для апроксимації похідної за часом у вузлах першого часового шару використаємо центральну симетричну різницю:
. Для апроксимації похідної за часом у вузлах першого часового шару використаємо центральну симетричну різницю:
 .
. . Щоб виключити значення функції у фіктивному вузлі
. Щоб виключити значення функції у фіктивному вузлі  :
: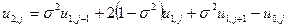
 (4.4)
(4.4) .
. й
й  зі швидкістю
зі швидкістю  . При
. При  метод стає нестійким. Останнє означає, що при продовженні обчислень похибки катастрофічно наростають.
метод стає нестійким. Останнє означає, що при продовженні обчислень похибки катастрофічно наростають. ,
,  ,
, .
. й по
й по 
 .
.
 ) після перетворень прийме вигляд:
) після перетворень прийме вигляд: .
. . Перевіримо цю нерівність при заданих умовах задачі:
. Перевіримо цю нерівність при заданих умовах задачі:  , тобто схема може бути стійкою, але краще було б взяти крок за часом менше.
, тобто схема може бути стійкою, але краще було б взяти крок за часом менше. ,
,  ,
,  ,
,  ,
,  ,
,  .
. ,
,  ;
;  ,
,  ;
; 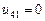 ,
,  .
. , тоді
, тоді 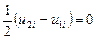 , отже
, отже  . Тобто для
. Тобто для  :
:  ,
,  ,
,  ,
,  .
.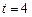 :
: ;
; ;
; ;
; .
.
 . Крок за часом оберемо в 4 рази менше
. Крок за часом оберемо в 4 рази менше  . Розрахунок з меншими кроками дасть нам можливість перевірити точність розв'язку за правилом Рунге.
. Розрахунок з меншими кроками дасть нам можливість перевірити точність розв'язку за правилом Рунге.
 , наведений на рис. 4.4. Початкове положення струни показане на графіку суцільною лінією, інші графіки відповідають моментам часу 2, 4 і 6.
, наведений на рис. 4.4. Початкове положення струни показане на графіку суцільною лінією, інші графіки відповідають моментам часу 2, 4 і 6.
 і
і  наведені на рис. 4.5.
наведені на рис. 4.5.

 ,
,  , відносна майже 3,9%. Якщо така точність незадовільна, треба ще зменшити кроки.
, відносна майже 3,9%. Якщо така точність незадовільна, треба ще зменшити кроки. , та другу похідну по
, та другу похідну по  .
.

 . Отримали такі результати:
. Отримали такі результати: , що складає майже 8% від значення функції. Якщо ж виконати розрахунки з кроками ще в 2 рази менше, то погрішність зменшиться до 0.03.
, що складає майже 8% від значення функції. Якщо ж виконати розрахунки з кроками ще в 2 рази менше, то погрішність зменшиться до 0.03.



