
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача для самостійного розв'язку на практиціСодержание книги
Поиск на нашем сайте Задача 4.1. Знайти розв'язок крайової задачі для рівняння
с початковими умовами: і граничними умовами: Завдання до лабораторної роботи Завдання 4.1. Використовуючи метод сіток, розв'язати змішану задачу для рівняння коливання струни Завдання 4.2. Знайти наближений розв'язок задачі завдання 4.1 за допомогою неявної різницевої схеми. Порівняти отримані результати. Варіанти індивідуальних завдань
Завдання 4.3. Коливання тонкої пластини, якщо не враховувати втрати на тертя, описуються нормованим хвильовим рівнянням виду: Варіанти індивідуальних завдань
Рисунок 4.7 – Область розв'язку завдання 4.3 4.6 Контрольні питання Які особливості чисельного розв'язку диференціальних рівнянь гіперболічного типу? 3. Які види сіток використовуються в методі кінцевих різниць? Яким чином будують на цих сітках різницеві апроксимації й відповідні їм шаблони? 4. Як задаються граничні умови? З яких міркувань вибирають крок сітки в методі кінцевих різниць? 5. Яким чином можна оцінити погрішність результату чисельного розв'язку? 6. Що таке стійкість різницевої схеми? Приведіть приклади стійких і нестійких різницевих схем. 7. У яких випадках може виникати нестійкість розв'язку задачі? Як впливає вибір параметрів сітки на стійкість? 8. Що розуміють під збіжністю процесу розв'язку задачі? 9. Назвіть три основних джерела погрішностей при розв'язку задач на ЕОМ, їх природу й способи зменшення.
Методи розв'язку інтегральних рівнянь Загальні відомості про інтегральні рівняння Визначення 1. Інтегральним рівнянням називається рівняння щодо невідомої функції, яка знаходиться під знаком інтеграла. Визначення 2. Лінійним інтегральним рівнянням Фредгольма називаються рівняння виду
(рівняння 2-го роду) і
(рівняння 1-го роду). В (5.1) і (5.2) Будемо припускати, що межі інтегрування
Якщо Звичайно розглядають сімейство рівнянь
залежних від числового параметра Метод послідовних наближень розв'язку інтегральних рівнянь Фредгольма Розглянемо випадок, коли число
За умови (5.6) рівняння (5.5) має єдиний розв'язок, який може бути знайдений методом послідовних наближень. Перепишемо рівняння (5.5) у вигляді:
і, вибравши довільне нульове наближення
Якщо число Приклад 5.1. Методом послідовних наближень розв'язати рівняння Розв'язок. Покладемо
і, отже, умова
У загальному випадку
Звідки
Точним розв'язком рівняння є функція При чисельній реалізації вважається, що послідовність функцій Погрішність
де
Кількість кроків (наближень) суттєво залежить від вибору початкового наближення, тобто від близькості його до шуканого розв'язку.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 489; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 ,
,  ,
, 
 ,
, 
 ,
,  .
. з початковими умовами
з початковими умовами  ,
,  ,
, 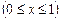 , і крайовими умовами
, і крайовими умовами  ,
,  . Розв'язок виконати із кроком
. Розв'язок виконати із кроком  ;
;  . Знайти наближений розв'язок задачі за допомогою явної різницевої схеми. Виконати розрахунки з половинним кроком за часом і довжині струни й оцінити точність отриманого розв'язку.
. Знайти наближений розв'язок задачі за допомогою явної різницевої схеми. Виконати розрахунки з половинним кроком за часом і довжині струни й оцінити точність отриманого розв'язку.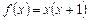 ,
,
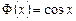 ,
,
 ,
,
 .
.
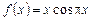 ,
,
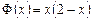 ,
,
 ,
,
 .
.

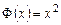 ,
,
 ,
, 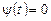

 ,
,
 ,
,
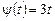
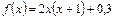

 ,
,


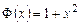 ,
,

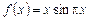
 ,
, 
 ,
, 
 ,
,
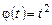 ,
, 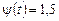

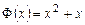


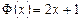
 ,
,  ,
,
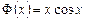
 ,
, 
 ,
,
 ,
,
 ,
, 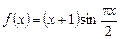
 ,
,
 ,
, 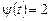
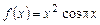
 ,
,
 ,
, 

 ,
,
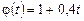 ,
,
 .
.
 ,
,
 ,
,
 ,
,

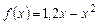 ,
,
 ,
,


 ,
,  ,
,

 ,
,
 ,
,
 .
.
 , де
, де  – деформація пластини,
– деформація пластини,  – координати,
– координати,  – час. Розрахуйте коливання при заданих у таблиці розмірах
– час. Розрахуйте коливання при заданих у таблиці розмірах  і
і  , граничних
, граничних  ,
,  ,
,  ,
,  і початкових
і початкових  і
і  умовах. Використовувати PDE Tools пакета MATLAB.
умовах. Використовувати PDE Tools пакета MATLAB.

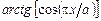
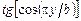





 (5.1)
(5.1) (5.2)
(5.2) – невідома функція, а ядро
– невідома функція, а ядро  й вільний член
й вільний член  передбачаються заданими відповідно у квадраті
передбачаються заданими відповідно у квадраті  й на відрізку
й на відрізку  .
. й
й  в (5.1) – кінцеві числа, а функції
в (5.1) – кінцеві числа, а функції  , (5.3)
, (5.3) . (5.4)
. (5.4)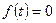 всюди на
всюди на  , що обертає це рівняння в тотожність відносно
, що обертає це рівняння в тотожність відносно  .
. , (5.5)
, (5.5) .
. (5.6)
(5.6)
 , побудуємо послідовність
, побудуємо послідовність  ,
, 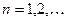 , за формулою:
, за формулою: ,
, 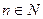 .
.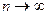 послідовність
послідовність  .
.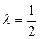 й
й  . Маємо
. Маємо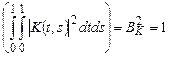
 виконана. Прийнявши
виконана. Прийнявши  , послідовно знаходимо:
, послідовно знаходимо: ,
,

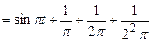 .
. .
. .
. , у чому можна переконатися безпосередньою перевіркою.
, у чому можна переконатися безпосередньою перевіркою. , де
, де 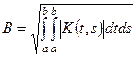 .
. -го наближення визначається нерівністю:
-го наближення визначається нерівністю: ,
,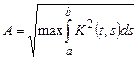 ,
, 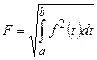 ,
,  .
.


