
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Квадратурные формулы наивысшей алгебраической степени точностиСодержание книги
Поиск на нашем сайте
Постараемся повысить точность квадратурной формулы, используя неравномерное расположение узлов. Поставим задачу: построить квадратурную формулу
которая при заданном n была бы точна для многочлена возможно большей степени. Такие формулы называют квадратурными формулами наивысшей алгебраической степени точности или формулами Гаусса. Как обычно,
Условия (12.30) представляют собой нелинейную систему из m+1 уравнений относительно Выпишем отдельно уравнение для
Уравнение (12.31) можно рассматривать как уравнение нормировки коэффициентов квадратурной формулы (12.29). Рассмотрим примеры. Построим формулы Гаусса для разного числа узлов. Пусть имеем единичную весовую функцию Пример 12. 11. n=1. Получаем: Пример 12.12.n=2. В данном случае m=3 и система (12.30) включает четыре уравнения:
Решаем систему. Во втором и в четвертом уравнениях перенесем второе слагаемое в правую часть и поделим четвертое уравнение на первое. Получим:
точную для многочленов до третьей степени включительно. Обратим внимание, что из второго и четвертого уравнений (включающих нечетные степени x) следует только симметрия квадратурной формулы. Численные значения узлов и коэффициентов определяются из первого и третьего уравнений. Интересен геометрический смысл полученной формулы. Через две заданные точки:
Формула (12.32) может быть получена также из геометрических соображений. Ненулевой вклад в интеграл Опишем теперь площадь под кривой
т.е. чтобы значение параболы в точке
Проиллюстрируем эти рассуждения. Введем функцию  , равную 1 в узлах , равную 1 в узлах  независимо от значения параметра a. Соответственно, площадь под кривой независимо от значения параметра a. Соответственно, площадь под кривой  на отрезке на отрезке  равна 2. Графики функции равна 2. Графики функции  для двух значений параметра a показаны на рис.12.7а. На рис.12.7б показана функция для двух значений параметра a показаны на рис.12.7а. На рис.12.7б показана функция  , суммированная с нечетными функциями , суммированная с нечетными функциями 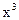 и и  . Как видно из значений интегралов, площадь под всеми четырьмя кривыми (с учетом знака) – одна и та же. Рисунки представляют собой активную вставку, созданную в среде Mathcad. . Как видно из значений интегралов, площадь под всеми четырьмя кривыми (с учетом знака) – одна и та же. Рисунки представляют собой активную вставку, созданную в среде Mathcad.
Пример 12.13. По формуле Гаусса с двумя узлами вычислим интеграл
и сравним найденное значение с точным. Точное значение интеграла легко вычисляется. После замены переменной имеем:
По формуле Гаусса Пример 12.14. Используя формулу Гаусса с двумя узлами, вычислим интеграл
Точное значение интеграла равно Чтобы применить формулу Гаусса, преобразуем отрезок интегрирования к стандартному отрезку
Вновь получаем, что формула Гаусса дает точное значение интеграла:
Пример 12.15. Построим формулу Гаусса с тремя узлами. Пусть по-прежнему
Поделив второе уравнение на первое, находим
находим Пример 12.16. Вычислим интеграл
По формуле Гаусса с двумя узлами (
Аналогично вычисляем по формуле Гаусса с тремя узлами:
Сравним полученные результаты с результатами расчетов по формуле Симпсона с тремя узлами:
Видим, что погрешность формулы Гаусса с тем же количеством узлов примерно в 70 раз меньше.
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 1169; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.43.200 (0.011 с.) |

 , (12.29)
, (12.29) обозначает весовую функцию, и
обозначает весовую функцию, и  – непрерывная функция. Для удобства нумеруем узлы от 1 до n. Потребуем, чтобы формула (1) была точна для любого алгебраического многочлена степени m. Это эквивалентно требованию, чтобы формула была точной для функций:
– непрерывная функция. Для удобства нумеруем узлы от 1 до n. Потребуем, чтобы формула (1) была точна для любого алгебраического многочлена степени m. Это эквивалентно требованию, чтобы формула была точной для функций:  Получаем условия:
Получаем условия: (12.30)
(12.30)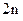 неизвестных:
неизвестных:  Число уравнений равно числу неизвестных, если
Число уравнений равно числу неизвестных, если 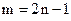 . Это число определяет наивысшую степень многочлена, для которого формула (12.29) является точной.
. Это число определяет наивысшую степень многочлена, для которого формула (12.29) является точной. :
: (12.31)
(12.31)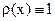 (иначе говоря, весовая функция отсутствует) и стандартный, симметричный относительно начала координат, отрезок интегрирования
(иначе говоря, весовая функция отсутствует) и стандартный, симметричный относительно начала координат, отрезок интегрирования 
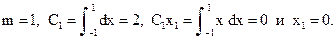 Приходим к формуле прямоугольников:
Приходим к формуле прямоугольников:  Формула прямоугольников точна для любого многочлена первой степени.
Формула прямоугольников точна для любого многочлена первой степени.
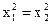 , или
, или 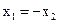 – узлы расположены симметрично. Учитывая симметрию, получаем из второго уравнения:
– узлы расположены симметрично. Учитывая симметрию, получаем из второго уравнения:  . Из первого уравнения следует, что
. Из первого уравнения следует, что  Наконец из третьего уравнения находим:
Наконец из третьего уравнения находим: 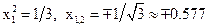 . Получаем квадратурную формулу
. Получаем квадратурную формулу , (12.32)
, (12.32) – можно провести бесчисленное множество кривых третьего порядка
– можно провести бесчисленное множество кривых третьего порядка  . Как следует из найденной квадратурной формулы, площади, заключенные между осью x и любой из этих кривых, и ограниченные вертикальными линиями
. Как следует из найденной квадратурной формулы, площади, заключенные между осью x и любой из этих кривых, и ограниченные вертикальными линиями  , одинаковы и равны
, одинаковы и равны  .
.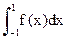 вносят лишь четные функции:
вносят лишь четные функции:  и
и  . Интеграл в симметричных пределах от нечетных функций
. Интеграл в симметричных пределах от нечетных функций  равен нулю. Чтобы квадратурная формула правильно учитывала нулевой вклад в интеграл нечетных функций
равен нулю. Чтобы квадратурная формула правильно учитывала нулевой вклад в интеграл нечетных функций  . Разместим узел
. Разместим узел  таким образом, чтобы выполнялось равенство:
таким образом, чтобы выполнялось равенство: –
– (коэффициент
(коэффициент  не играет роли). Отсюда
не играет роли). Отсюда 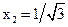 . Значение параболы в симметричном узле
. Значение параболы в симметричном узле  даст вторую половину площади. Ясно, что те же самые отсчеты описывают также значение площади, ограниченной линией постоянной высоты
даст вторую половину площади. Ясно, что те же самые отсчеты описывают также значение площади, ограниченной линией постоянной высоты  . Приходим, таким образом вновь к формуле (12.32).
. Приходим, таким образом вновь к формуле (12.32).
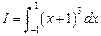
 .
. . Поскольку формула Гаусса с двумя узлами точна для любого многочлена степени m =3, получаем точное значение.
. Поскольку формула Гаусса с двумя узлами точна для любого многочлена степени m =3, получаем точное значение.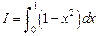 .
. .
. . Полагаем:
. Полагаем: .
. .
. Чтобы избежать необходимости решения системы из шести уравнений, используем геометрические соображения. Формула с тремя узлами точна для многочлена степени
Чтобы избежать необходимости решения системы из шести уравнений, используем геометрические соображения. Формула с тремя узлами точна для многочлена степени 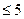 . Поскольку интеграл от x в нечетной степени равен нулю, достаточно построить квадратурную формулу, точную для функций
. Поскольку интеграл от x в нечетной степени равен нулю, достаточно построить квадратурную формулу, точную для функций  . Эти функции показаны на рис. 12.8. Из соображений симметрии заключаем, что два узла должны быть расположены симметрично, и один узел должен находиться в центре:
. Эти функции показаны на рис. 12.8. Из соображений симметрии заключаем, что два узла должны быть расположены симметрично, и один узел должен находиться в центре:  Для описания функций
Для описания функций  достаточно рассмотреть половину отрезка интегрирования
достаточно рассмотреть половину отрезка интегрирования  должен полностью описывать площадь под кривыми
должен полностью описывать площадь под кривыми  :
:

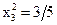 , или
, или  . С учетом найденного значения из первого уравнения получаем
. С учетом найденного значения из первого уравнения получаем  . Отсчет в точке
. Отсчет в точке  необходим для описания площади, ограниченной линией
необходим для описания площади, ограниченной линией  . Из условия нормировки
. Из условия нормировки
 .
. , используя формулу Гаусса с двумя и тремя узлами. Точное значение интеграла легко вычисляется:
, используя формулу Гаусса с двумя и тремя узлами. Точное значение интеграла легко вычисляется:  . Чтобы привести отрезок интегрирования к стандартному отрезку [-1,1], заменим переменную интегрирования:
. Чтобы привести отрезок интегрирования к стандартному отрезку [-1,1], заменим переменную интегрирования:
 ) получаем:
) получаем: , и погрешность равна
, и погрешность равна  .
. , и погрешность равна 0.0014.
, и погрешность равна 0.0014. , погрешность равна 0.094.
, погрешность равна 0.094.


